15 연속형 변수 가설검정
| Z-검정 | t-검정 | |
|---|---|---|
| 조건 | 모집단 표준편차 알려져 있음 | 모집단 표준편차 알려져 있지 않음 |
| 사용되는 분포 | 정규 분포 | t 분포 |
| 필요한 정보 | 모표준편차 | 표본 표준편차 |
| 적합한 표본 크기 | 큰 표본 (n > 30) | 작은 표본 (일반적으로 n ≤ 30) |
| 주요 사용 예 | 제품 무게 검정 등 공장 생산 제품의 품질 관리 | 소규모 연구나 학급의 평균 성적 추정 |
15.1 단일 모집단
추론 통계학에서 단일 모집단 추정은 하나의 모집단에 대한 통계적 추론을 다룬다. 모집단의 특성을 파악하고, 표본으로부터 얻은 정보를 바탕으로 모집단에 대한 결론을 도출하는 과정으로 단일 모집단 추정에서는 주로 모평균에 대한 가설 검정과 신뢰구간 추정을 수행한다.
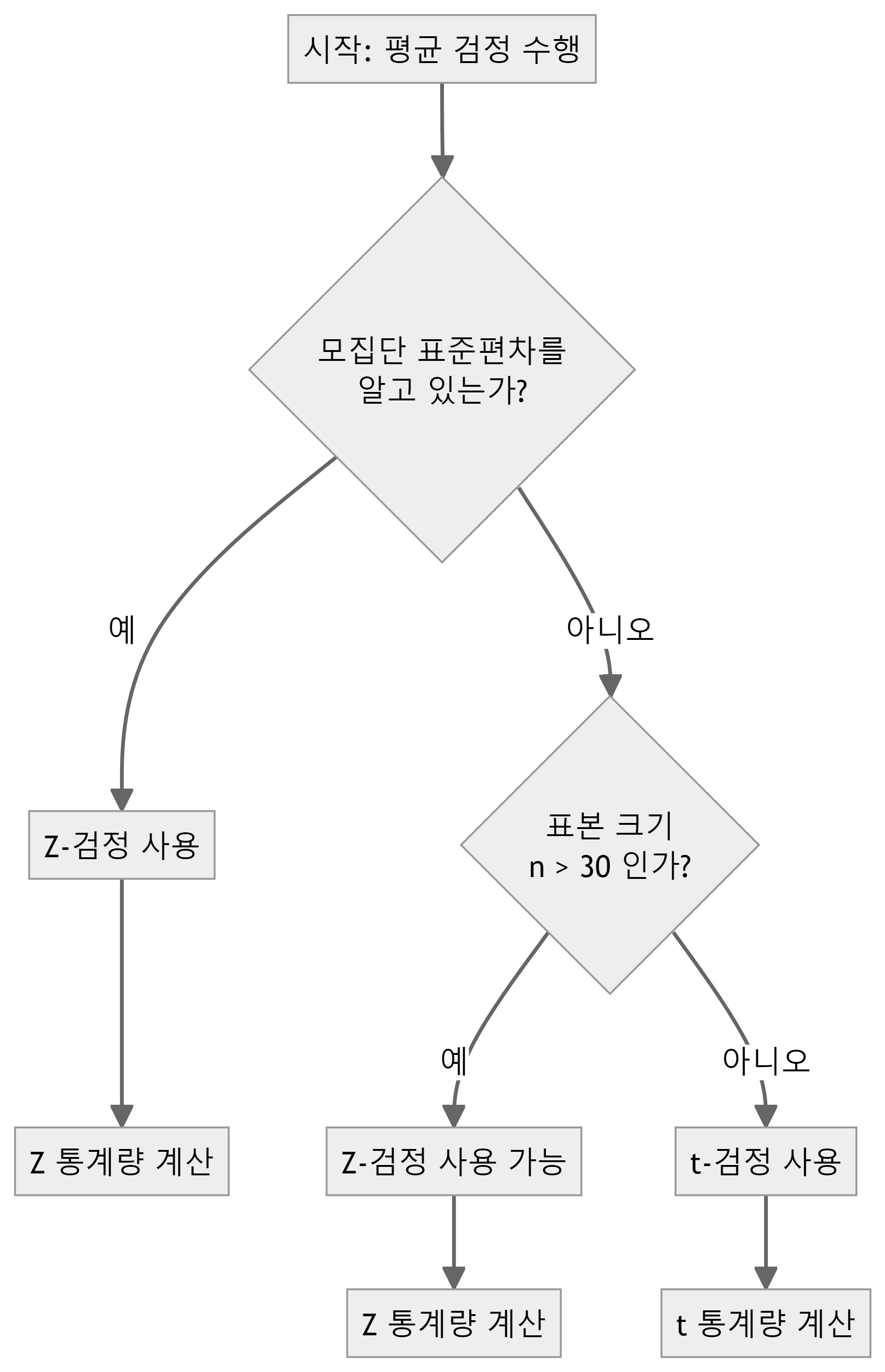
모평균에 대한 가설 검정은 모집단의 평균이 특정 값과 같은지, 다른지를 판단하는 것이다. 이때 귀무가설(\(H_0\))과 대립가설(\(H_1\))을 설정하고, 표본 평균(\(\bar{x}\))과 표본 표준편차(\(s\))를 이용하여 검정통계량을 계산한다. 모집단이 정규분포를 따르고 모분산(\(\sigma^2\))을 알고 있는 경우에는 z-검정을, 모분산을 모르는 경우에는 t-검정을 사용한다.
모평균에 대한 가설과 z-검정의 검정통계량은 다음과 같이 계산한다.
- 귀무 가설 \(H_0\): \(\mu = \mu_0\)
- 대립 가설 \(H_1\): \(\mu \neq \mu_0\), \(\mu > \mu_0\) 또는 \(\mu < \mu_0\)
\[z = \frac{\bar{x} - \mu_0}{\sigma / \sqrt{n}}\]
\(\mu_0\)는 귀무가설에서 주장하는 모평균 값이고, \(n\)은 표본의 크기이다.
모평균에 대한 가설과 t-검정의 검정통계량은 다음과 같이 계산한다.
- 귀무 가설 \(H_0\): \(\mu = \mu_0\)
- 대립 가설 \(H_1\): \(\mu \neq \mu_0\), \(\mu > \mu_0\) 또는 \(\mu < \mu_0\)
\[t = \frac{\bar{x} - \mu_0}{s / \sqrt{n}}\]
이 검정통계량은 자유도가 \(n-1\)인 t-분포를 따른다.
계산된 검정통계량을 기준으로 p-값을 계산하고 유의수준(\(\alpha\))과 비교하여 귀무가설의 기각 여부를 결정한다. 만약 p-값이 유의수준보다 작다면 귀무가설을 기각하고 대립가설을 채택한다.
모평균에 대한 신뢰구간 추정은 표본 평균을 중심으로 일정 범위를 구하고, 그 안에 모평균이 포함될 확률을 나타낸다. z-검정에서의 신뢰구간은 다음과 같이 계산한다.
\(\bar{x} \pm z_{\alpha/2} \cdot \frac{\sigma}{\sqrt{n}}\)
t-검정에서의 신뢰구간은 다음과 같이 계산한다.
\(\bar{x} \pm t_{\alpha/2} \cdot \frac{s}{\sqrt{n}}\)
\(z_{\alpha/2}\)와 \(t_{\alpha/2}\)는 각각 표준정규분포와 t-분포에서 유의수준 \(\alpha\)에 해당하는 임계값이다.
단일 모집단 문제에서는 표본의 크기가 충분히 크거나(\(n \geq 30\)), 모집단이 정규분포를 따른다는 가정이 필요하다. 만약 이러한 가정이 만족되지 않는다면 비모수 검정 방법을 고려해야 한다. 통계적 검정을 통해 데이터가 제시하는 현상이 우연에 의한 것인지 아니면 실제로 유의미한 차이나 패턴을 반영하는 것인지를 결정할 수 있다.
15.1.1 사례
단일표본 t-검정
1908년 윌리엄 시얼리 고셋(William Sealy Gosset)은 기네스 맥주로 잘 알려진 기네스 브루어리(Guinness Brewery)에서 일하면서 작은 표본 크기로 맥아의 품질을 평가하는 문제를 연구했다. 연구 결과는 현재 우리가 알고 있는 t-분포와 t-검정으로 이어졌다.
고셋의 데이터를 사용하여 단일 표본 t-검정을 수행하면 귀무가설은 맥아의 평균 함량이 3.0%라는 것이고, 대립가설은 평균 함량이 3.0%와 다르다는 것이다.
데이터: 3.0, 3.0, 2.9, 2.8, 3.1, 3.2, 3.1, 2.9, 3.0, 3.1
- \(H_0: \mu = 3.0\) (맥아의 평균 함량이 3.0%)
- \(H_1: \mu \neq 3.0\) (맥아의 평균 함량이 3.0%와 다름)
표본 평균 \(\bar{x}\): \(\bar{x} = \frac{\sum_{i=1}^{n} x_i}{n} = \frac{3.0 + 3.0 + 2.9 + 2.8 + 3.1 + 3.2 + 3.1 + 2.9 + 3.0 + 3.1}{10} = 3.01\)
표본 표준편차 \(s\): \(s = \sqrt{\frac{\sum_{i=1}^{n} (x_i - \bar{x})^2}{n-1}} = 0.119721899973787\)
검정 통계량 \(t\): \(t = \frac{\bar{x} - \mu_0}{s / \sqrt{n}} = 0.264135271897681\)
- \(n = 10\) (표본의 크기)
- \(\mu_0 = 3.0\) (귀무가설에서의 모평균)
p-값이 유의수준 0.05보다 크므로 귀무가설을 기각하지 않는다. 즉, 이 데이터에 근거하면 맥아의 평균 함량이 3.0%와 유의하게 다르다고 할 수 없다.
R에서는 내장된 t.test() 함수를 사용하여 t-검정을 수행할 수 있다. t.test() 함수를 통해 수행된 결과를 통해 위에서 계산한 결과와 동일한 결과를 얻을 수 있음을 확인할 수 있다.
단일표본 z-검정
단일표본 z-검정은 모집단의 표준편차를 알고 있을 때 사용한다. 모집단의 표준편차를 알고 있을 때는 z-검정을 사용하는 것이 더 정확하다.
한 피자 가게에서는 피자 도우의 평균 직경이 10인치가 되도록 설정하고 있다. 품질관리팀은 생산된 피자 도우의 직경이 목표 평균인 10인치와 유의한 차이가 있는지 검정하고자 한다.
과거 데이터로부터 피자 도우 직경의 모분산이 0.16 제곱인치로 알려져 있다. 품질관리팀은 36개의 피자 도우를 랜덤하게 선택하여 직경을 측정하였고, 그 결과는 다음과 같다.
데이터(피자 도우 직경, 인치): 9.8, 9.6, 10.2, 9.7, 9.9, 10.1, 9.8, 9.7, 10.0, 9.9, 9.6, 9.8, 10.1, 9.9, 9.7, 10.0, 9.8, 9.9, 10.2, 9.8, 9.7, 9.9, 10.0, 9.8, 9.9, 9.7, 10.1, 9.8, 9.9, 10.0, 9.8, 9.9, 10.1, 9.7, 9.8, 10.0
- \(H_0: \mu = 10\) (피자 도우 직경의 평균은 10인치다.)
- \(H_1: \mu \neq 10\) (피자 도우 직경의 평균은 10인치와 다르다.)
검정통계량 Z는 다음과 같이 계산한다.
\[Z = \frac{\bar{X} - \mu}{\sigma / \sqrt{n}}\]
- \(\bar{X}\): 표본평균
- \(\mu\): 귀무가설 하의 모평균 (10)
- \(\sigma\): 모표준편차 (0.4, \(\sqrt{0.16}\))
- \(n\): 표본크기 (36)
r length(pizza_diameters)개 피자 도우 직경 측정 데이터를 바탕으로 계산한 표본평균은 r sample_mean인치이며, Z-검정 결과 p-값은 r p_value로 나타났다. 이는 유의수준 0.05보다 크므로 귀무가설을 기각하지 않는다.
즉, 이 데이터에 근거할 때 피자 도우 직경의 평균이 목표치인 10인치와 유의하게 다르다고 할 수 없다. 하지만 p-값이 0.05에 근접하므로, 품질관리팀은 피자 도우 생산 공정을 지속적으로 모니터링하고 필요한 경우 개선 조치를 취할 수 있다.
R에서는 내장된 z-검정 함수가 없어 BSDA 패키지 z.test() 함수를 사용하여 z-검정을 수행할 수 있다. z.test() 함수를 통해 수행된 결과를 통해 위에서 계산한 결과와 동일한 결과를 얻을 수 있음을 확인할 수 있다.
15.1.2 shiny 앱
#| label: shinylive-testing-tz
#| viewerHeight: 600
#| standalone: true
library(shiny)
library(ggplot2)
ui <- fluidPage(
titlePanel("z-검정과 t-검정"),
sidebarLayout(
sidebarPanel(
h3("사용 설명"),
p("z-검정과 t-검정을 수행하고 p-값을 시각화합니다."),
p("1. 검정 유형을 선택하세요."),
p("2. 선택한 검정 유형에 맞는 데이터를 입력하세요. 데이터는 쉼표로 구분됩니다."),
p("3. z-검정의 경우, 모표준편차를 입력하세요. t-검정의 경우, 모표준편차 입력은 무시됩니다."),
p("4. 가설 검정을 위한 모평균 값을 입력하세요."),
p("5. 양측 검정 또는 단측 검정을 선택하세요."),
p("6. 유의수준(alpha)을 선택하세요."),
p("7. 결과 해석 탭에서 검정 결과와 p-값 시각화를 확인하세요."),
radioButtons("test_type", "검정 유형:",
choices = c("z-검정" = "z_test", "t-검정" = "t_test")),
conditionalPanel(
condition = "input.test_type == 'z_test'",
textAreaInput("data_z", "z-검정 데이터 입력 (쉼표로 구분):", rows = 3,
value = "9.8, 9.6, 10.2, 9.7, 9.9, 10.1, 9.8, 9.7, 10.0, 9.9, 9.6, 9.8, 10.1, 9.9, 9.7, 10.0, 9.8, 9.9, 10.2, 9.8, 9.7, 9.9, 10.0, 9.8, 9.9, 9.7, 10.1, 9.8, 9.9, 10.0, 9.8, 9.9, 10.1, 9.7, 9.8, 10.0"),
numericInput("pop_sd", "모표준편차 (z-검정용):", value = 0)
),
conditionalPanel(
condition = "input.test_type == 't_test'",
textAreaInput("data_t", "t-검정 데이터 입력 (쉼표로 구분):", rows = 3,
value = "3.0, 3.0, 2.9, 2.8, 3.1, 3.2, 3.1, 2.9, 3.0, 3.1")
),
numericInput("mu0", "가설 검정을 위한 모평균 값:", value = 0),
radioButtons("alternative", "대립 가설:",
choices = c("양측 검정" = "two.sided", "단측 검정 (왼쪽)" = "less", "단측 검정 (오른쪽)" = "greater")),
selectInput("alpha", "유의수준(alpha):",
choices = c(0.01, 0.05, 0.1), selected = 0.05)
),
mainPanel(
tabsetPanel(
tabPanel("결과", uiOutput("result")),
tabPanel("결과 해석", plotOutput("plot"))
)
)
)
)
server <- function(input, output) {
test_result <- reactive({
test_type <- input$test_type
mu0 <- input$mu0
alternative <- input$alternative
alpha <- as.numeric(input$alpha)
if (test_type == "z_test") {
data <- as.numeric(unlist(strsplit(input$data_z, ",")))
pop_sd <- input$pop_sd
z_score <- (mean(data) - mu0) / (pop_sd / sqrt(length(data)))
p_value <- switch(alternative,
"two.sided" = 2 * pnorm(abs(z_score), lower.tail = FALSE),
"less" = pnorm(z_score),
"greater" = pnorm(z_score, lower.tail = FALSE))
list(z_score = z_score, p_value = p_value, alpha = alpha, n = length(data), mean = mean(data), sd = pop_sd)
} else {
data <- as.numeric(unlist(strsplit(input$data_t, ",")))
t_score <- (mean(data) - mu0) / (sd(data) / sqrt(length(data)))
p_value <- switch(alternative,
"two.sided" = 2 * pt(abs(t_score), df = length(data) - 1, lower.tail = FALSE),
"less" = pt(t_score, df = length(data) - 1),
"greater" = pt(t_score, df = length(data) - 1, lower.tail = FALSE))
list(t_score = t_score, p_value = p_value, alpha = alpha, n = length(data), mean = mean(data), sd = sd(data))
}
})
output$result <- renderUI({
test_type <- input$test_type
if (test_type == "z_test") {
withMathJax(
paste0(
"표본 수 (n): $$", test_result()$n, "$$", br(),
"표본 평균 ($\\bar{x}$): $$", round(test_result()$mean, 4), "$$", br(),
"모표준편차 ($\\sigma$): $$", round(test_result()$sd, 4), "$$", br(),
"검정 통계량 (Z): $$", round(test_result()$z_score, 4), "$$", br(),
"p-값: $$", round(test_result()$p_value, 4), "$$"
)
)
} else {
withMathJax(
paste0(
"표본 수 (n): $$", test_result()$n, "$$", br(),
"표본 평균 ($\\bar{x}$): $$", round(test_result()$mean, 4), "$$", br(),
"표본 표준편차 ($s$): $$", round(test_result()$sd, 4), "$$", br(),
"검정 통계량 (t): $$", round(test_result()$t_score, 4), "$$", br(),
"p-값: $$", round(test_result()$p_value, 4), "$$"
)
)
}
})
output$plot <- renderPlot({
test_type <- input$test_type
alternative <- input$alternative
alpha <- as.numeric(input$alpha)
if (test_type == "z_test") {
z_score <- test_result()$z_score
p_value <- test_result()$p_value
if (alternative == "two.sided") {
plot_data <- data.frame(x = c(-4, 4))
critical_z <- qnorm(1 - alpha/2)
ggplot(plot_data, aes(x)) +
stat_function(fun = dnorm, n = 101, args = list(mean = 0, sd = 1)) +
geom_area(stat = "function", fun = dnorm, fill = "red", alpha = 0.5,
xlim = c(-4, -critical_z), args = list(mean = 0, sd = 1)) +
geom_area(stat = "function", fun = dnorm, fill = "red", alpha = 0.5,
xlim = c(critical_z, 4), args = list(mean = 0, sd = 1)) +
geom_vline(xintercept = z_score, color = "blue", linetype = "dashed") +
geom_vline(xintercept = -critical_z, color = "black") +
geom_vline(xintercept = critical_z, color = "black") +
labs(title = "정규 분포와 z-score",
x = "z-score",
y = "밀도")
} else if (alternative == "less") {
plot_data <- data.frame(x = c(-4, 4))
critical_z <- qnorm(alpha)
ggplot(plot_data, aes(x)) +
stat_function(fun = dnorm, n = 101, args = list(mean = 0, sd = 1)) +
geom_area(stat = "function", fun = dnorm, fill = "red", alpha = 0.5,
xlim = c(-4, critical_z), args = list(mean = 0, sd = 1)) +
geom_vline(xintercept = z_score, color = "blue", linetype = "dashed") +
geom_vline(xintercept = critical_z, color = "black") +
labs(title = "정규 분포와 z-score",
x = "z-score",
y = "밀도")
} else {
plot_data <- data.frame(x = c(-4, 4))
critical_z <- qnorm(1 - alpha)
ggplot(plot_data, aes(x)) +
stat_function(fun = dnorm, n = 101, args = list(mean = 0, sd = 1)) +
geom_area(stat = "function", fun = dnorm, fill = "red", alpha = 0.5,
xlim = c(critical_z, 4), args = list(mean = 0, sd = 1)) +
geom_vline(xintercept = z_score, color = "blue", linetype = "dashed") +
geom_vline(xintercept = critical_z, color = "black") +
labs(title = "정규 분포와 z-score",
x = "z-score",
y = "밀도")
}
} else {
t_score <- test_result()$t_score
p_value <- test_result()$p_value
df <- length(as.numeric(unlist(strsplit(input$data_t, ",")))) - 1
if (alternative == "two.sided") {
plot_data <- data.frame(x = c(-4, 4))
critical_t <- qt(1 - alpha/2, df)
ggplot(plot_data, aes(x)) +
stat_function(fun = dt, n = 101, args = list(df = df)) +
geom_area(stat = "function", fun = dt, fill = "red", alpha = 0.5,
xlim = c(-4, -critical_t), args = list(df = df)) +
geom_area(stat = "function", fun = dt, fill = "red", alpha = 0.5,
xlim = c(critical_t, 4), args = list(df = df)) +
geom_vline(xintercept = t_score, color = "blue", linetype = "dashed") +
geom_vline(xintercept = -critical_t, color = "black") +
geom_vline(xintercept = critical_t, color = "black") +
labs(title = "t 분포와 t-score",
x = "t-score",
y = "밀도")
} else if (alternative == "less") {
plot_data <- data.frame(x = c(-4, 4))
critical_t <- qt(alpha, df)
ggplot(plot_data, aes(x)) +
stat_function(fun = dt, n = 101, args = list(df = df)) +
geom_area(stat = "function", fun = dt, fill = "red", alpha = 0.5,
xlim = c(-4, critical_t), args = list(df = df)) +
geom_vline(xintercept = t_score, color = "blue", linetype = "dashed") +
geom_vline(xintercept = critical_t, color = "black") +
labs(title = "t 분포와 t-score",
x = "t-score",
y = "밀도")
} else {
plot_data <- data.frame(x = c(-4, 4))
critical_t <- qt(1 - alpha, df)
ggplot(plot_data, aes(x)) +
stat_function(fun = dt, n = 101, args = list(df = df)) +
geom_area(stat = "function", fun = dt, fill = "red", alpha = 0.5,
xlim = c(critical_t, 4), args = list(df = df)) +
geom_vline(xintercept = t_score, color = "blue", linetype = "dashed") +
geom_vline(xintercept = critical_t, color = "black") +
labs(title = "t 분포와 t-score",
x = "t-score",
y = "밀도")
}
}
})
}
shinyApp(ui, server)
15.2 두 모집단 검정
두 모집단 검정은 서로 다른 두 모집단의 특성을 비교하는 것을 목표로 한다. 두 모집단의 평균, 분산, 비율 등을 비교하여 두 모집단 간의 차이가 통계적으로 유의한지를 판단하는 과정으로 대표적으로 독립 2표본 검정과 대응 2표본 검정을 들 수 있다.
독립 2표본 검정은 서로 독립인 두 모집단에서 추출한 표본을 비교하는 방법으로 두 모집단의 분산이 알려져 있는지 여부에 따라 다르게 적용된다.
- 두 모집단의 분산이 알려져 있고 같다고 가정할 때는 2표본 z-검정을 사용하고 검정통계량 Z는 다음과 같이 계산한다.
\(Z = \frac{(\bar{X_1} - \bar{X_2}) - (μ_1 - μ_2)}{\sqrt{\frac{σ_1^2}{n_1} + \frac{σ_2^2}{n_2}}}\)
- 두 모집단의 분산이 알려져 있지 않거나 다르다고 가정할 때는 2표본 t-검정을 사용한다. 이때, 두 모집단의 분산이 같다고 가정하면 합동 분산(pooled variance)을 사용하고, 다르다고 가정하면 비합동 분산(unpooled variance)을 사용하고 검정통계량 t는 다음과 같이 계산한다.
\(t = \frac{(\bar{X_1} - \bar{X_2}) - (μ_1 - μ_2)}{\sqrt{\frac{s_1^2}{n_1} + \frac{s_2^2}{n_2}}}\)
대응 2표본 검정(paired two-sample test)은 동일한 개체나 그룹에 대해 두 가지 처리를 적용하고, 그 차이를 분석하는 방법이다. 대응 2표본 검정에서는 두 표본의 차이를 계산하여 단일 표본 검정을 수행한다.
\(H_0: μ_d = 0\) (두 모집단의 차이의 평균이 0이다) \(H_1: μ_d ≠ 0\) (두 모집단의 차이의 평균이 0이 아니다)
\(\bar{d}\)는 표본 차이의 평균, \(μ_d\)는 모집단 차이의 평균(대개 0), \(s_d\)는 표본 차이의 표준편차, \(n\)은 표본 크기, 검정통계량 t는 다음과 같이 계산한다.
\(t = \frac{\bar{d} - μ_d}{s_d / \sqrt{n}}\)
두 모집단 문제에 대한 검정은 다양한 분야에서 활용된다. 예를 들어, 두 가지 다른 약물의 효과를 비교하거나, 두 집단의 성적을 비교하는 등의 상황에서 사용할 수 있다. 두 모집단 문제를 해결하기 위해서는 적절한 검정 방법을 선택하고, 가정을 확인하며, 결과를 해석하는 과정이 필요하다.
15.2.1 사례: 독립 2표본
두 가지 다른 학습방법이 학업에 미치는 영향을 알아보기 위해 독립 2표본 t-검정을 통해 확인해보자. 두 가지 다른 학습 방법(A, B)이 학생들의 수학 점수에 미치는 영향을 비교한다고 가정하자. 각 학습 방법을 적용한 학생들의 수학 점수는 다음과 같다.
데이터:
- 학습 방법 A: 85, 92, 78, 88, 90, 82, 95, 87, 83, 89
- 학습 방법 B: 80, 85, 90, 75, 88, 92, 87, 83, 79, 81
- 가설 설정:
- \(H_0: μ_A = μ_B\) (두 학습 방법의 평균 점수는 같다)
- \(H_1: μ_A ≠ μ_B\) (두 학습 방법의 평균 점수는 다르다)
- 표본 평균 계산:
- \(\bar{X_A} = \frac{85 + 92 + 78 + 88 + 90 + 82 + 95 + 87 + 83 + 89}{10} = 86.9\)
- \(\bar{X_B} = \frac{80 + 85 + 90 + 75 + 88 + 92 + 87 + 83 + 79 + 81}{10} = 84.0\)
- 표본 분산 계산:
- \(s_A^2 = \frac{\sum_{i=1}^{n_A} (X_{A,i} - \bar{X_A})^2}{n_A - 1} = 25.43333\)
- \(s_B^2 = \frac{\sum_{i=1}^{n_B} (X_{B,i} - \bar{X_B})^2}{n_B - 1} = 28.66667\)
- 검정통계량 t 계산:
- \(t = \frac{(\bar{X_A} - \bar{X_B}) - (μ_A - μ_B)}{\sqrt{\frac{s_A^2}{n_A} + \frac{s_B^2}{n_B}}} = \frac{86.9 - 84.0}{2.429} = 1.2468\)
- 자유도 계산:
- \(df = \frac{(\frac{s_A^2}{n_A} + \frac{s_B^2}{n_B})^2}{(\frac{s_A^2}{n_A})^2 / (n_A-1) + (\frac{s_B^2}{n_B})^2 / (n_B-1)} = 18\)
- p-값 계산:
양측 검정이므로, p-값은 \(P(|T| > |t|) = 0.2284\)이다. 따라서 p-값이 0.05보다 크므로 귀무가설을 기각하지 않는다. 따라서 두 학습 방법 간의 평균 점수 차이는 통계적으로 유의하지 않다고 결론내릴 수 있다.
15.2.2 사례: 대응 2표본
두 가지 다른 학습방법이 학업에 미치는 영향을 알아보기 위해 이번에는 대응 2표본 t-검정을 수행하는 과정을 살펴보자. 10명의 학생들을 대상으로 새로운 수학 학습 방법을 적용하기 전과 후의 점수를 비교하여, 이 학습 방법의 효과를 확인한다.
| 학생 | 학습 전 점수 | 학습 후 점수 |
|---|---|---|
| 1 | 75 | 80 |
| 2 | 82 | 85 |
| 3 | 88 | 92 |
| 4 | 79 | 84 |
| 5 | 83 | 87 |
| 6 | 90 | 95 |
| 7 | 85 | 89 |
| 8 | 78 | 83 |
| 9 | 92 | 96 |
| 10 | 87 | 90 |
- 가설 설정:
- \(H_0: μ_d = 0\) (학습 전후의 평균 점수 차이는 0이다)
- \(H_1: μ_d ≠ 0\) (학습 전후의 평균 점수 차이는 0이 아니다)
- 점수 차이 계산:
| 학생 | 점수 차이 (학습 후 - 학습 전) |
|---|---|
| 1 | 5 |
| 2 | 3 |
| 3 | 4 |
| 4 | 5 |
| 5 | 4 |
| 6 | 5 |
| 7 | 4 |
| 8 | 5 |
| 9 | 4 |
| 10 | 3 |
- 차이의 평균 (\(\bar{d}\)) 계산
\(\bar{d} = \frac{5 + 3 + 4 + 5 + 4 + 5 + 4 + 5 + 4 + 3}{10} = 4.2\)
- 차이의 표준편차 (\(s_d\)) 계산:
\(s_d = \sqrt{\frac{\sum_{i=1}^{n} (d_i - \bar{d})^2}{n - 1}} = 0.789\)
- 검정통계량 t 계산:
\(t = \frac{\bar{d} - μ_d}{s_d / \sqrt{n}} = \frac{4.2 - 0}{0.789 / \sqrt{10}} = 16.837\)
자유도 계산: \(df = n - 1 = 9\)
p-값 계산: 양측 검정이므로, p-값은 \(P(|T| > |t|) = 0.0000000412 \quad (4.12e-08)\)이다.
p-값이 0.05보다 매우 작으므로 귀무가설을 기각한다. 따라서 새로운 수학 학습 방법을 적용한 후 학생들의 점수가 통계적으로 유의하게 향상되었다고 결론내릴 수 있다. 대응 2표본 t-검정을 사용하여 동일한 개체나 그룹에 대해 두 가지 처리를 적용하고, 그 차이를 분석할 수 있다.
15.2.3 shiny 앱
#| label: shinylive-testing-two-sample
#| viewerHeight: 600
#| standalone: true
library(shiny)
library(tidyverse)
library(DT)
ui <- fluidPage(
titlePanel("독립 2표본 t-검정과 대응 2표본 t-검정"),
sidebarLayout(
sidebarPanel(
h3("설명"),
p("독립 2표본 t-검정과 대응 2표본 t-검정을 수행합니다."),
p("1. 검정 유형을 선택하세요."),
p("2. 선택한 검정 유형에 맞는 데이터를 쉼표로 구분하여 입력하세요."),
p("3. 대립가설을 선택하세요."),
p("4. 유의 수준을 선택하세요."),
p("5. 독립 2표본 t-검정의 경우, 두 집단의 분산이 같은지 여부를 선택하세요."),
p("6. 결과, 입력 데이터, 그래프 탭에서 결과를 확인하세요."),
radioButtons("test_type", "검정 유형 선택:",
c("독립 2표본 t-검정" = "independent",
"대응 2표본 t-검정" = "paired")),
conditionalPanel(
condition = "input.test_type == 'independent'",
textInput("sample1", "표본 1 (쉼표로 구분):", "85, 92, 78, 88, 90, 82, 95, 87, 83, 89"),
textInput("sample2", "표본 2 (쉼표로 구분):", "80, 85, 90, 75, 88, 92, 87, 83, 79, 81"),
checkboxInput("var_equal", "두 집단의 분산이 같다고 가정", value = TRUE)
),
conditionalPanel(
condition = "input.test_type == 'paired'",
textInput("before", "학습 전 점수 (쉼표로 구분):", "75, 82, 88, 79, 83, 90, 85, 78, 92, 87"),
textInput("after", "학습 후 점수 (쉼표로 구분):", "80, 85, 92, 84, 87, 95, 89, 83, 96, 90")
),
radioButtons("alternative", "대립가설:",
c("양측 검정" = "two.sided",
"단측 검정 (왼쪽)" = "less",
"단측 검정 (오른쪽)" = "greater")),
selectInput("sig_level", "유의 수준:",
c("0.01" = 0.01, "0.05" = 0.05, "0.10" = 0.10),
selected = "0.05")
),
mainPanel(
tabsetPanel(
tabPanel("입력 데이터",
DTOutput("table")
),
tabPanel("결과",
verbatimTextOutput("result"),
h4("검정 결과 해석"),
textOutput("interpretation")
),
tabPanel("그래프",
plotOutput("plot")
)
)
)
)
)
server <- function(input, output, session) {
t_test_result <- reactive({
if (input$test_type == "independent") {
sample1 <- as.numeric(unlist(strsplit(input$sample1, ",")))
sample2 <- as.numeric(unlist(strsplit(input$sample2, ",")))
t.test(sample1, sample2, alternative = input$alternative, conf.level = 1 - as.numeric(input$sig_level), var.equal = input$var_equal)
} else {
before <- as.numeric(unlist(strsplit(input$before, ",")))
after <- as.numeric(unlist(strsplit(input$after, ",")))
t.test(after, before, paired = TRUE, alternative = input$alternative, conf.level = 1 - as.numeric(input$sig_level))
}
})
output$result <- renderPrint({
t_test_result()
})
output$interpretation <- renderText({
if (t_test_result()$p.value < as.numeric(input$sig_level)) {
"귀무가설을 기각합니다. 두 집단 간에 유의한 차이가 있습니다."
} else {
"귀무가설을 기각하지 않습니다. 두 집단 간에 유의한 차이가 없습니다."
}
})
input_data <- reactive({
if (input$test_type == "independent") {
data.frame(
표본1 = as.numeric(unlist(strsplit(input$sample1, ","))),
표본2 = as.numeric(unlist(strsplit(input$sample2, ",")))
)
} else {
data.frame(
학습전 = as.numeric(unlist(strsplit(input$before, ","))),
학습후 = as.numeric(unlist(strsplit(input$after, ",")))
)
}
})
output$table <- renderDT({
datatable(input_data())
})
output$plot <- renderPlot({
if (input$test_type == "independent") {
sample1 <- as.numeric(unlist(strsplit(input$sample1, ",")))
sample2 <- as.numeric(unlist(strsplit(input$sample2, ",")))
df <- data.frame(
value = c(sample1, sample2),
group = factor(rep(c("표본1", "표본2"), c(length(sample1), length(sample2))))
)
ggplot(df, aes(x = group, y = value, fill = group)) +
geom_boxplot() +
labs(x = "표본", y = "값") +
theme_minimal()
} else {
before <- as.numeric(unlist(strsplit(input$before, ",")))
after <- as.numeric(unlist(strsplit(input$after, ",")))
df <- data.frame(
subject = factor(rep(1:length(before), 2)),
value = c(before, after),
group = factor(rep(c("학습전", "학습후"), each = length(before)))
)
ggplot(df, aes(x = group, y = value, color = group)) +
geom_line(aes(group = subject)) +
geom_point() +
labs(x = "학습", y = "값") +
theme_minimal()
}
})
}
shinyApp(ui, server)