23 이산형 확률분포
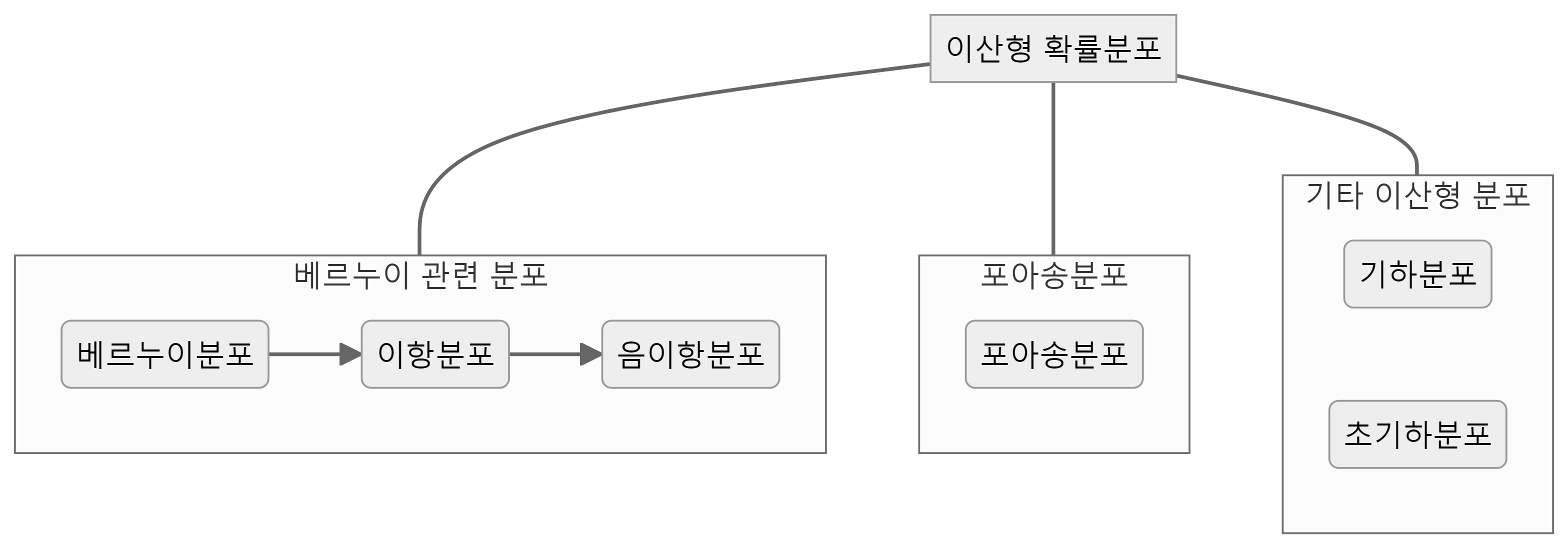
이산형 확률분포(discrete probability distribution)는 확률변수가 가질 수 있는 값이 유한하거나 셀 수 있는 무한한 경우의 확률분포로 정의된다. 대표적인 이산형 확률분포로 베르누이분포, 이항분포, 포아송분포를 들 수 있다.
23.1 베르누이분포
베르누이분포(Bernoulli distribution)는 가장 간단한 이산형 확률분포 중 하나로, 단 두 가지 가능한 결과(성공 또는 실패)만을 가지는 시행을 모형화한 것이다. 동전 던지기에서 앞면이 나오는 경우를 대표적으로 들 수 있다.
확률변수 \(X\)가 베르누이분포를 따른다고 할 때, 성공할 확률을 \(p\)라 하면 확률질량함수(PMF)는 다음과 같이 정의된다.
\[P(X = x) = p^x(1-p)^{1-x} \qquad x = 0, 1\]
평균 \(E(X) = p\)이고 분산 \(Var(X) = p(1-p)\) 이다.
베르누이분포 누적분포함수(CDF)는 확률변수 \(X\)가 특정 값 이하일 확률로 정의되고, 베르누이분포 CDF는 다음과 같다.
\[ \begin{align*} F(x) &= P(X \leq x) \\ \newline F(x) &= \begin{cases} 0 & \text{if } x < 0 \\ 1-p & \text{if } 0 \leq x < 1 \\ 1 & \text{if } x \geq 1 \end{cases} \end{align*} \]
- \(x < 0\) 일 때: \(F(x) = 0\) 이 되는 것은 확률변수 \(X\)가 0보다 작은 값을 취할 수 없기 때문이다.
- \(0 \leq x < 1\) 일 때: \(X\)가 0 또는 1의 값을 취할 수 있으며, \(X = 0\) 일 확률이 \(1-p\)이므로, \(x\)가 0과 1 사이일 때 \(F(x)\)의 값은 \(1-p\)이 된다.
- \(x \geq 1\) 일 때: \(F(x) = 1\) 이 되는 이유는 \(X\)가 1 이상의 값을 취할 수 있는 최대 확률이 1이기 때문이다.
23.2 이항분포
이항분포(Binomial distribution)는 베르누이분포의 확장으로, \(n\)번의 독립적인 베르누이 시행에서 성공의 횟수를 모형화한 것이다. 예를 들어, 동전을 10번 던져 앞면이 나오는 횟수의 분포를 생각해 볼 수 있다.
확률변수 \(X\)가 이항분포를 따른다고 할 때, 시행 횟수 \(n\)과 각 시행의 성공 확률 \(p\)가 주어지면 확률질량함수는 다음과 같다.
\[P(X = k) = \binom{n}{k} p^k(1-p)^{n-k} \qquad k = 0, 1, ..., n\]
평균 \(E(X) = np\)이고 분산 \(Var(X) = np(1-p)\) 이다.
이항계수(binomial coefficient)는 \(\binom{n}{k}\) 으로 다음과 같이 정의된다.
\[\binom{n}{k} = \frac{n!}{k!(n-k)!}\]
이항분포의 누적분포함수(CDF)는 확률변수 \(X\)가 특정 값 이하일 확률을 표현하고 이항분포의 CDF는 다음과 같이 정의된다.
\[F(x) = P(X \leq x) = \sum_{k=0}^{\lfloor x \rfloor} \binom{n}{k} p^k(1-p)^{n-k}\]
\(\lfloor x \rfloor\)는 \(x\)의 바닥 함수(floor function)로, \(x\)보다 작거나 같은 최대의 정수를 나타낸다.
23.3 포아송분포
포아송분포(Poisson distribution)는 일정 시간 또는 공간 내에서 독립적으로 발생하는 사건의 횟수를 모형화한 것이다. 단위 시간 또는 공간 내에서 사건이 발생할 평균 횟수를 \(\lambda\)라고 할 때, 확률변수 X가 포아송분포를 따르면 확률질량함수는 다음과 같다.
\[P(X = k) = \frac{e^{-\lambda}\lambda^k}{k!} \text{ for } k = 0, 1, 2, ...\]
\(e\)는 자연상수(약 2.71828…)이고, \(k!\)는 k의 계승(factorial)을 나타낸다.
포아송분포의 누적분포함수(CDF)는 확률변수 \(X\)가 특정 값 이하일 확률을 나타내고 포아송분포 CDF는 다음과 같이 정의된다.
\(F(x) = P(X \leq x) = e^{-\lambda} \sum_{k=0}^{\lfloor x \rfloor} \frac{\lambda^k}{k!}\)
\(\lfloor x \rfloor\)는 x의 바닥 함수(floor function)로, \(x\)보다 작거나 같은 최대의 정수를 나타낸다.
평균 \(E(X) = \lambda\)이고 분산 \(Var(X) = \lambda\) 이다.
포아송분포는 사건의 발생 횟수가 많지 않고 독립적일 때 적합한 확률모형으로 일정 시간 내 고장 발생 횟수, 일정 면적 내 나무의 개수 등을 모형화할 때 적합하다.