확률론
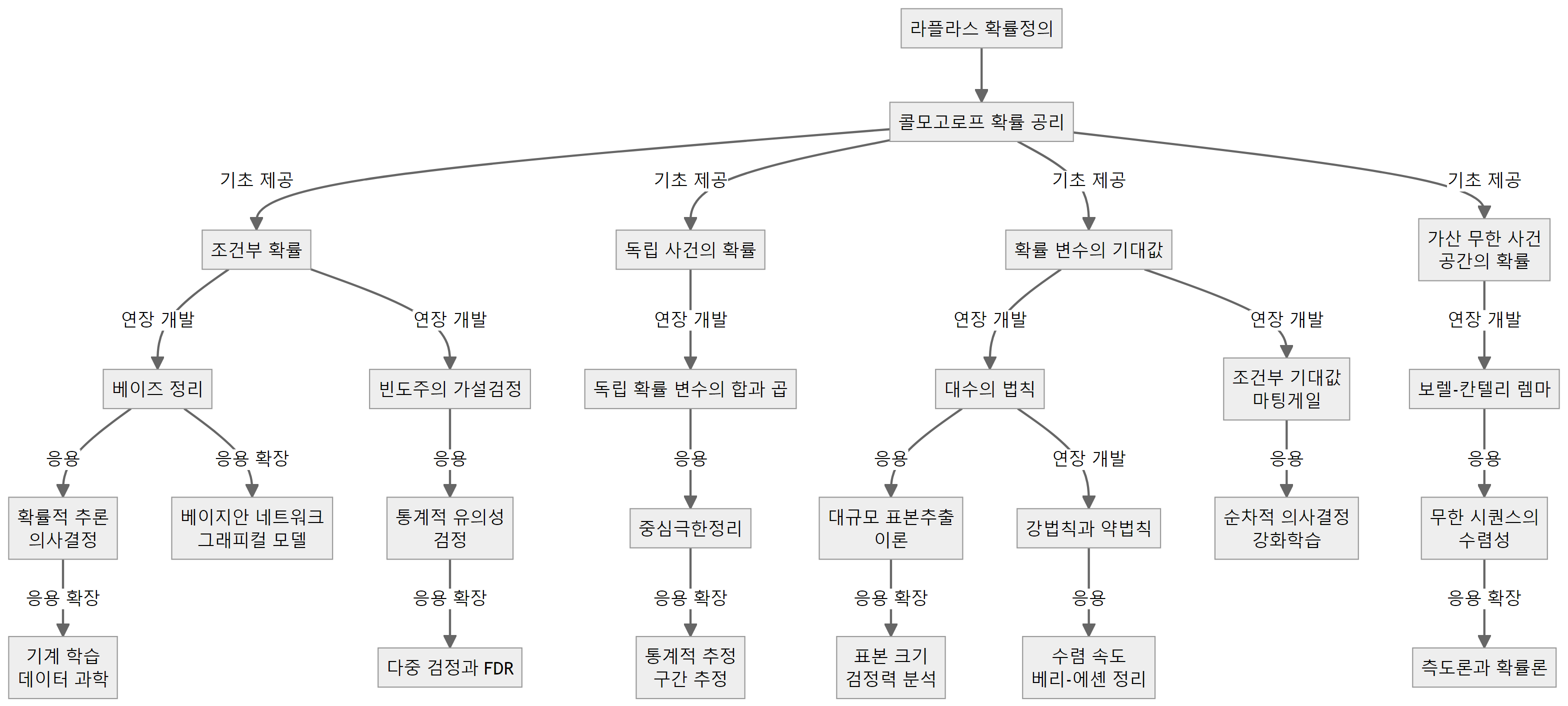
콜모고로프 확률 공리는 현대 확률론의 엄밀한 수학적 기반을 제공한다. 이 공리 체계는 측도론에 기반하여 확률을 공리적으로 정의하며, 세 가지 기본 규칙인 비음성, 규범화, 가산 무한 가법성으로 구성된다.
콜모고로프 확률 공리로부터 확률론의 기본 개념들이 정립된다. 조건부 확률은 어떤 사건이 주어졌을 때 다른 사건이 일어날 확률로 정의되며, 두 사건의 관계를 이해하는 데 핵심적이다. 독립 사건의 개념도 콜모고로프 확률 공리로부터 엄밀하게 정의되는데, 두 사건이 독립이라는 것은 한 사건의 발생 여부가 다른 사건의 발생 확률에 영향을 미치지 않음을 의미한다.
또한 확률 변수와 기대값의 개념도 콜모고로프 확률 공리에 기반하여 정의된다. 확률 변수는 표본공간에서 정의된 실수 값 함수로, 그 값에 따라 확률이 부여된다. 기대값은 확률 변수의 평균값으로 정의되며, 확률분포의 특성을 요약하는 중요한 수치이다.
콜모고로프 확률 공리는 또한 사건의 무한 배열, 즉 무한 차원의 확률 공간을 다룰 수 있는 틀을 제공한다. 이를 통해 극한 관련 법칙들, 예를 들어 대수의 법칙이나 중심극한정리 등을 엄밀하게 증명할 수 있으며, 가산 무한 사건 공간의 확률을 다룰 수 있게 된다.
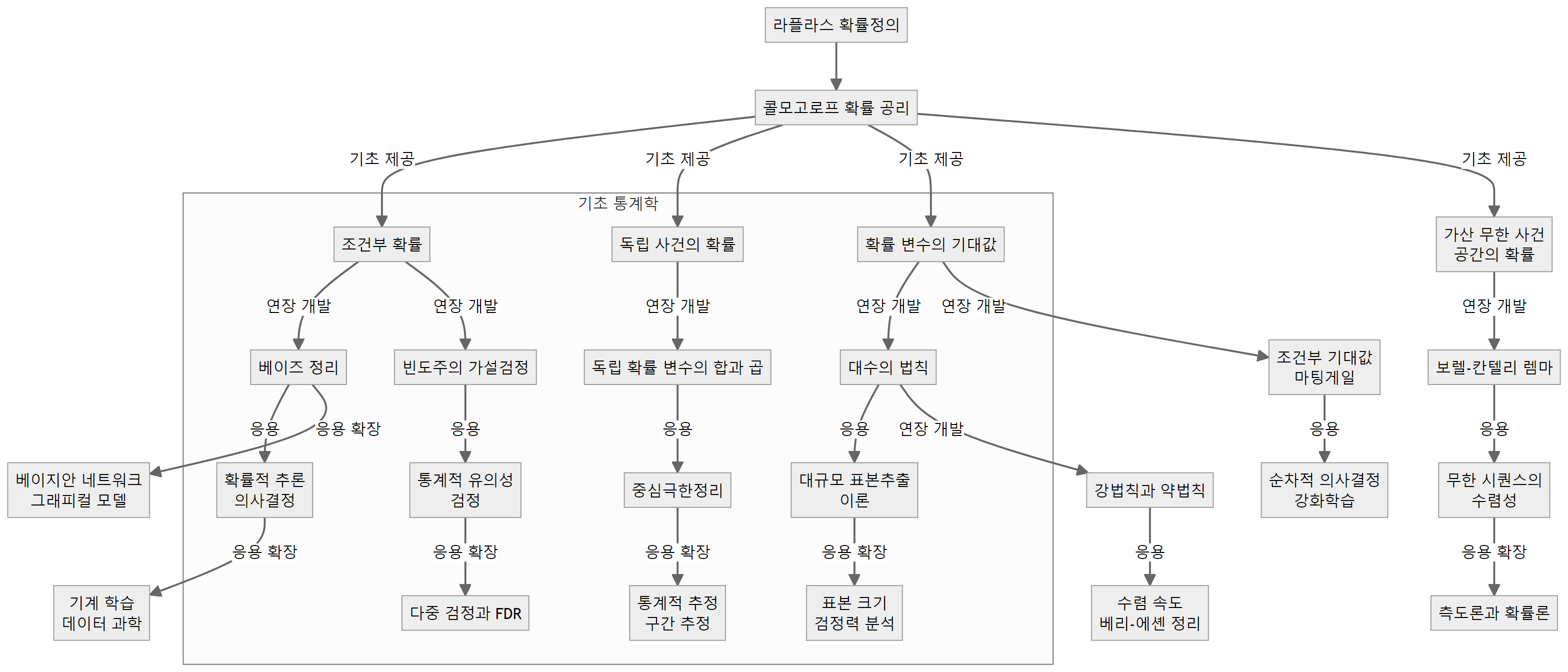
기초 통계학은 확률론의 기본 개념과 원리를 바탕으로 실제 데이터 분석에 필요한 통계적 방법론을 다루고 있다. 콜모고로프 확률 공리는 현대 확률론의 엄밀한 토대를 제공하지만, 그 자체로는 매우 추상적이고 일반적이어서 실제 데이터 분석에 직접 적용하기에는 어려움이 있다. 따라서 기초 통계학에서는 콜모고로프 확률 공리로부터 출발하여, 실제 데이터 분석에 유용하고 필수적인 개념과 방법론을 선별하여 중점적으로 다루게 된다.
기초 통계학에서 주로 다루는 주제들은 크게 확률의 기본 개념, 확률분포, 통계적 추정, 가설검정 등으로 나눌 수 있다. 조건부 확률, 베이즈 정리, 독립 사건 등은 확률의 기본 개념을 이해하는 데 필수적이며, 이를 바탕으로 확률분포와 확률변수의 성질을 공부하게 된다. 확률분포 중에서도 이항분포, 정규분포, 포아송 분포 등 데이터 분석에 자주 활용되는 분포들이 중점적으로 다뤄진다.
통계적 추정과 가설검정은 기초 통계학의 핵심 주제라고 할 수 있다. 중심극한정리와 대수의 법칙 등 표본 분포에 관한 이론을 바탕으로, 모평균 추정, 모비율 추정, 구간추정 등 다양한 통계적 추정 방법을 배우게 된다. 또한 가설검정의 기본 개념과 원리를 익힌 후, t-검정, 카이제곱 검정, F-검정 등 대표적인 통계적 검정 방법도 학습하게 된다.
이러한 주제들은 실제 데이터 분석에 직접 활용될 뿐만 아니라, 빅데이터 분석, 기계학습 등 응용 통계학의 기반이 되기 때문에 기초 통계학에서 반드시 다뤄야 할 내용이다. 또한 이런 방법론을 익히는 과정에서 통계적 사고력과 데이터 분석 능력을 기를 수 있다.
한편, 기초 통계학의 범위를 벗어나는 주제들도 있다. 예를 들어, 측도론, 마팅게일, 강화학습 등은 고급 확률론이나 전문 분야에서 다뤄지는 내용이다. 또한 수리통계학에서는 추정량의 점근적 성질, 최적 검정 등 통계적 방법론의 이론적 측면을 깊이 있게 탐구한다.
일원배치 분산분석
#> # A tibble: 3 × 7
#> term contrast null.value estimate conf.low conf.high adj.p.value
#> <chr> <chr> <dbl> <dbl> <dbl> <dbl> <dbl>
#> 1 종명칭 턱끈-아델리 0 10.0 8.98 11.0 5.82e-13
#> 2 종명칭 젠투-아델리 0 8.74 7.88 9.61 5.82e-13
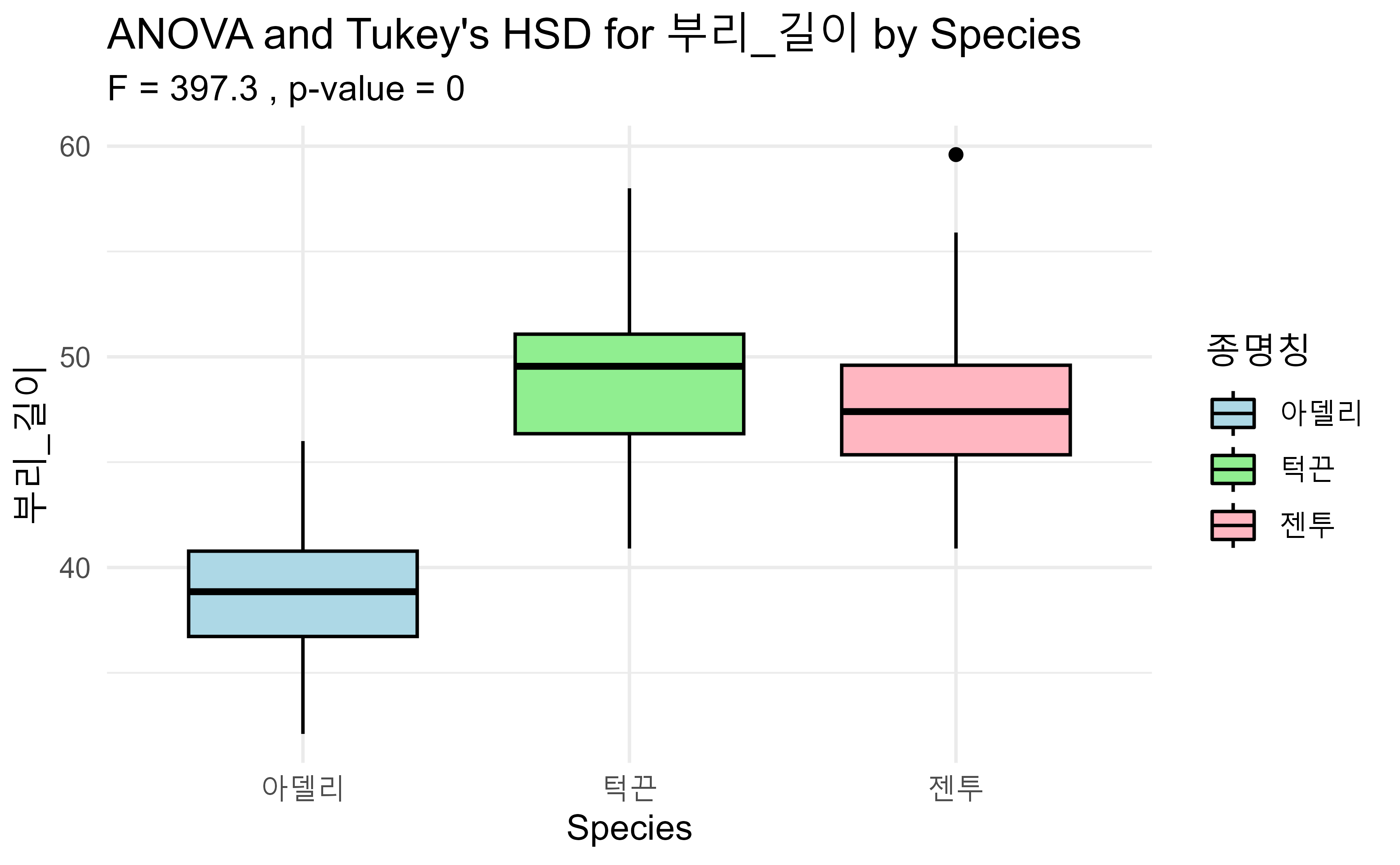
#> 3 종명칭 젠투-턱끈 0 -1.27 -2.33 -0.202 1.48e- 2펭귄 종에 따른 부리 길이 차이를 일원배치 분산분석(ANOVA)으로 검정하고, 사후 검정으로 투키 HSD 검정을 실시한 결과 펭귄 종 간 부리 길이에 유의한 차이가 있다고 결론 내릴 수 있고 사후 검정 결과 펭귄 종 간 부리 길이에 유의한 차이도 확인할 수 있다.
턱끈 펭귄의 부리 길이가 아델리 펭귄의 부리 길이보다 평균적으로 10.0mm 더 길다. 차이는 신뢰구간(8.98, 11.0)에서 유의하며, 조정된 p-value가 5.82e-13로 매우 작아 통계적으로 유의하다.
젠투 펭귄의 부리 길이가 아델리 펭귄의 부리 길이보다 평균적으로 8.74mm 더 길다. 차이 역시 신뢰구간(7.88, 9.61)에서 유의하며, 조정된 p-value가 5.82e-13로 매우 작아 통계적으로 유의하다.
젠투 펭귄의 부리 길이가 턱끈 펭귄의 부리 길이보다 평균적으로 1.27mm 더 짧다. 차이는 신뢰구간(-2.33, -0.202)에서 유의하며, 조정된 p-value가 1.48e-2로 0.05보다 작아 통계적으로 유의하다.
세 펭귄 종 간에는 부리 길이에 유의한 차이가 있음을 알 수 있고 구체적으로는 턱끈 펭귄의 부리가 가장 길고, 그 다음으로 젠투 펭귄, 아델리 펭귄 순으로 부리 길이가 짧다.
MANOVA는 다변량 종속 변수가 상호 연관되어 있고 이들 변수를 함께 분석해야 할 때 사용되는 방법으로 변수 간의 상호작용을 이해하고, 변수들이 집단 간에 어떻게 다른지 평가하는 데 유용하다. 복수의 ANOVA를 별도로 수행할 경우 제1종 오류의 위험이 증가하는데, MANOVA는 이러한 오류의 위험을 줄여 신뢰할 수 있는 통계적 결론을 도출하고, MANOVA는 독립 변수들 간의 상호작용 효과와 독립 변수와 종속 변수들 간의 상호작용 효과를 분석할 수 있어, 각 독립 변수가 종속 변수들에 미치는 영향이 어떻게 다른지 이해하는 데 중요하다.
MANOVA
마노바(MANOVA)는 여러 종속 변수가 관련된 경우 그룹 간 차이를 분석하는 것을 목표하는데, 몇 가지 중요한 전제조건을 충족해야 한다. 먼저, 모든 관측점은 서로 독립적이어야 하며 각 그룹에서 관찰된 데이터는 다변량 정규 분포를 따라야 하며, Shapiro-Wilk 검정과 같은 정규성 검정을 사용한다.
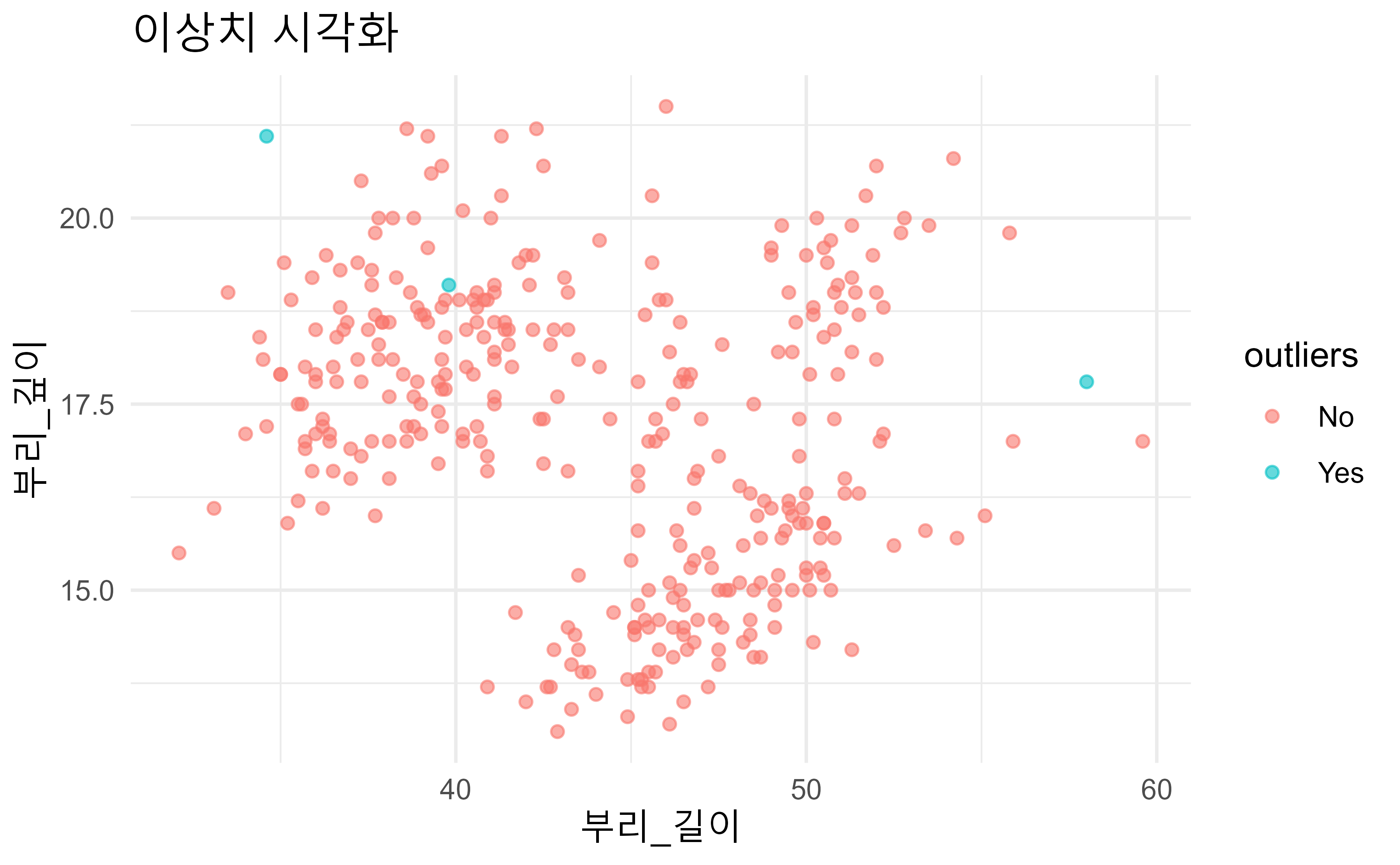
또한, 모든 그룹의 공분산 행렬은 동일해야 하는데, 이를 검증하기 위해 Box’s M 검정을 사용한다. 이상치는 결과에 영향을 줄 수 있기 때문에 데이터에 이상치가 없어야 하며, 상자그림이나 Mahalanobis 거리를 통해 이상치를 확인하고 제거한다.
정규성 검정
#> $부리_길이
#>
#> Shapiro-Wilk normality test
#>
#> data: x
#> W = 0.97434, p-value = 1.19e-05
#>
#>
#> $부리_깊이
#>
#> Shapiro-Wilk normality test
#>
#> data: x
#> W = 0.97329, p-value = 7.776e-06
#>
#>
#> $물갈퀴_길이
#>
#> Shapiro-Wilk normality test
#>
#> data: x
#> W = 0.95171, p-value = 5.393e-09
#>
#>
#> $체중
#>
#> Shapiro-Wilk normality test
#>
#> data: x
#> W = 0.95801, p-value = 3.568e-08
#> Test Statistic p value Result
#> 1 Mardia Skewness 127.42101776688 1.1855026472037e-17 NO
#> 2 Mardia Kurtosis -2.51762947836501 0.0118147535587461 NO
#> 3 MVN <NA> <NA> NO
#>
#> Box's M-test for Homogeneity of Covariance Matrices
#>
#> data: k_penguins[, c("부리_길이", "부리_깊이", "물갈퀴_길이", "체중")]
#> Chi-Sq (approx.) = 74.731, df = 20, p-value = 3.02e-08
#> [1] 3MANOVA 분석
#> Df Pillai approx F num Df den Df Pr(>F)
#> 종명칭 2 1.6379 370.89 8 656 < 2.2e-16 ***
#> Residuals 330
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> Response 부리_길이 :
#> Df Sum Sq Mean Sq F value Pr(>F)
#> 종명칭 2 7015.4 3507.7 397.3 < 2.2e-16 ***
#> Residuals 330 2913.5 8.8
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Response 부리_깊이 :
#> Df Sum Sq Mean Sq F value Pr(>F)
#> 종명칭 2 870.79 435.39 344.83 < 2.2e-16 ***
#> Residuals 330 416.67 1.26
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Response 물갈퀴_길이 :
#> Df Sum Sq Mean Sq F value Pr(>F)
#> 종명칭 2 50526 25262.9 567.41 < 2.2e-16 ***
#> Residuals 330 14693 44.5
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Response 체중 :
#> Df Sum Sq Mean Sq F value Pr(>F)
#> 종명칭 2 145190219 72595110 341.89 < 2.2e-16 ***
#> Residuals 330 70069447 212332
#> ---
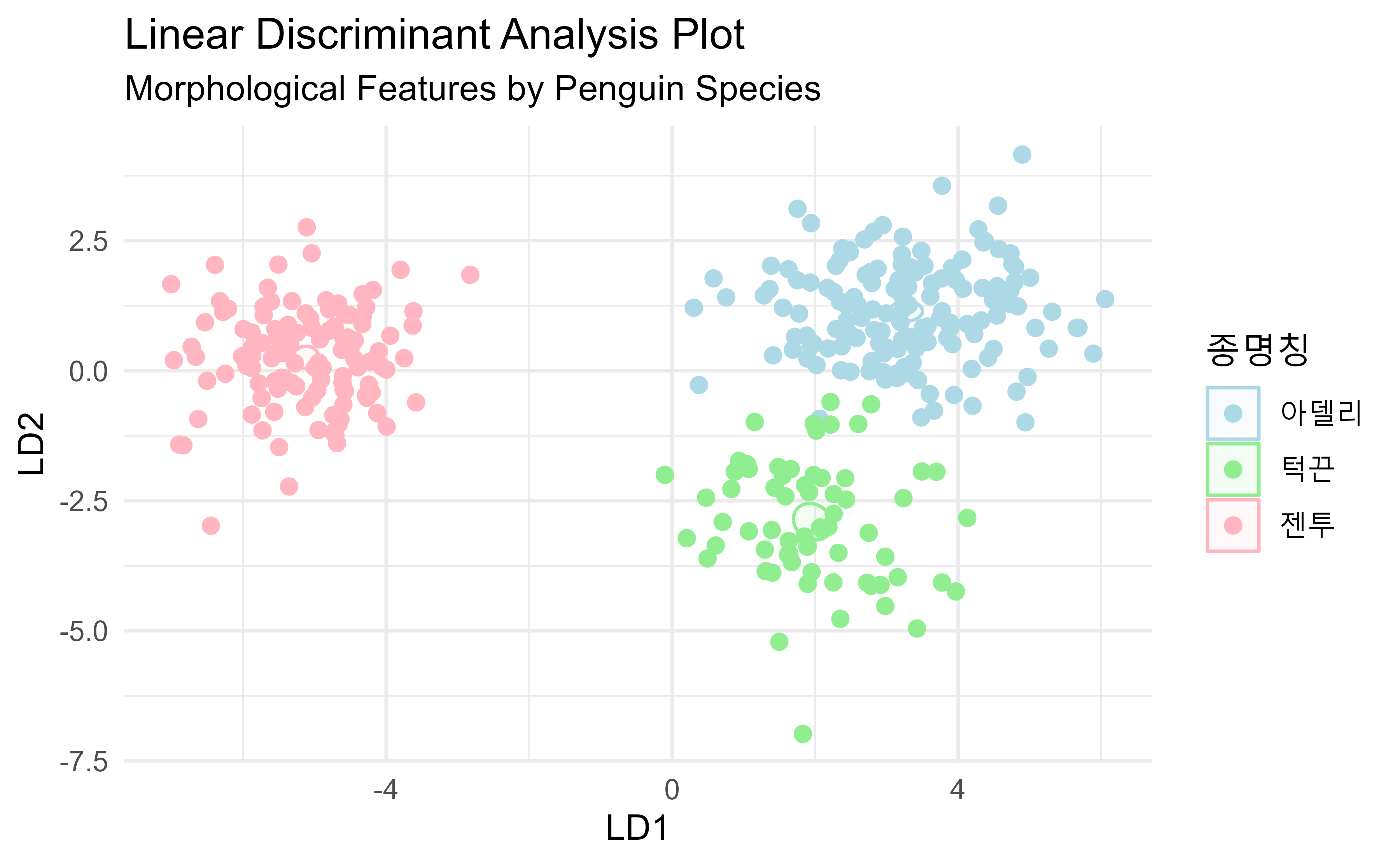
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1MANOVA (Multivariate Analysis of Variance) 결과를 선형판별분석(LDA, Linear Discriminant Analysis)로 시각화하는 이유는 LDA가 데이터의 그룹 간 차이를 가장 잘 나타내는 축을 찾아주기 때문이다. LDA는 데이터의 분산을 최대화하고, 그룹 간 분산을 최소화하는 방향으로 축을 설정하기 때문에, 다변량 분석에서 얻은 그룹 간 차이를 시각적으로 잘 드러내고 해석하기 좋은 도구로 평가받고 있다.
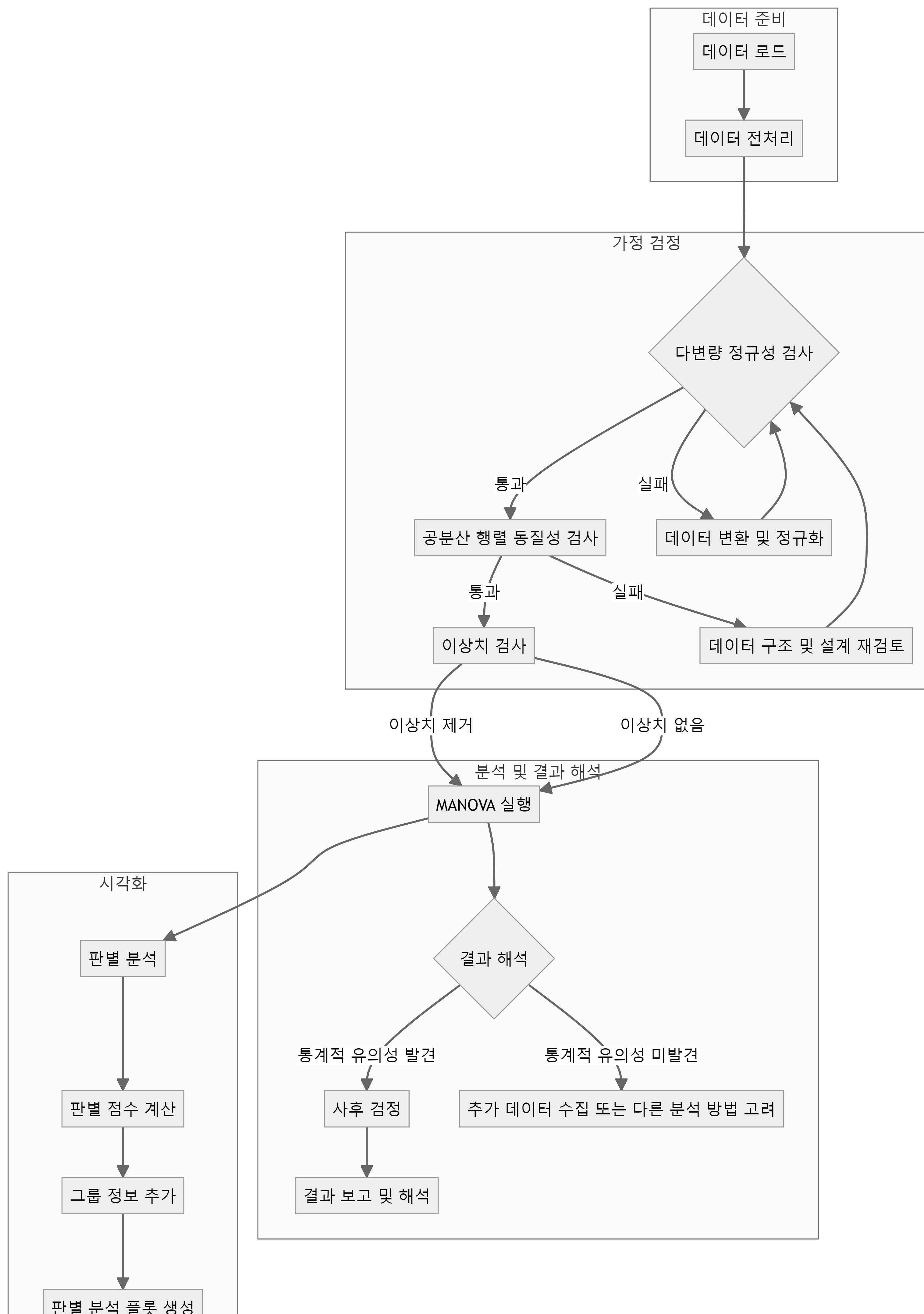
작업흐름
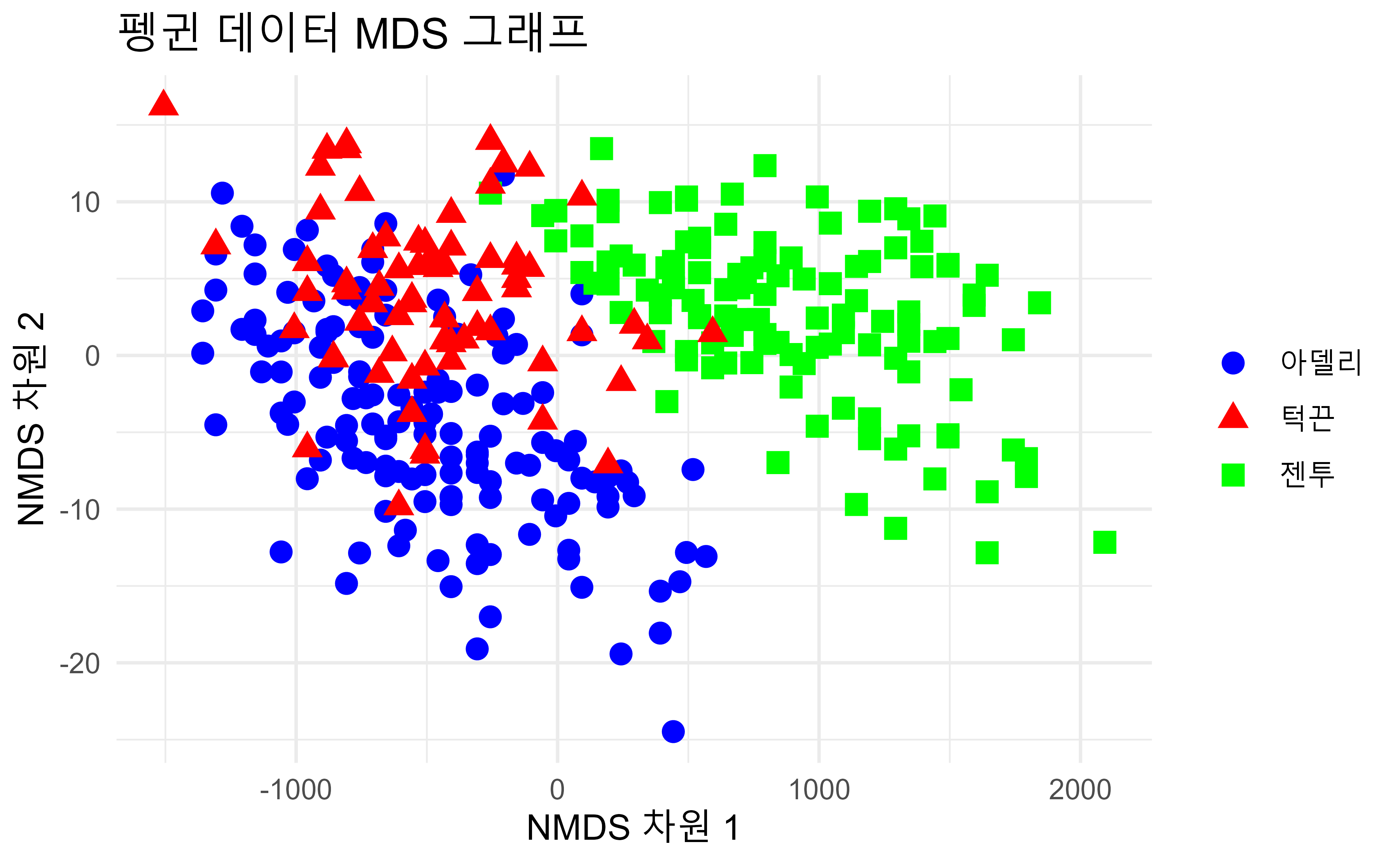
무가정 MANOVA
#> Permutation test for adonis under reduced model
#> Terms added sequentially (first to last)
#> Permutation: free
#> Number of permutations: 999
#>
#> adonis2(formula = distance_matrix ~ 종명칭, data = k_penguins, permutations = 999)
#> Df SumOfSqs R2 F Pr(>F)
#> 종명칭 2 145248631 0.67452 341.94 0.001 ***
#> Residual 330 70087470 0.32548
#> Total 332 215336101 1.00000
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> Run 0 stress 0.0002948723
#> Run 1 stress 0.0006127023
#> ... Procrustes: rmse 0.001396858 max resid 0.006951407
#> ... Similar to previous best
#> Run 2 stress 0.0006721258
#> ... Procrustes: rmse 0.002124365 max resid 0.007161177
#> ... Similar to previous best
#> Run 3 stress 0.0005839459
#> ... Procrustes: rmse 0.001195342 max resid 0.01119039
#> Run 4 stress 0.0005451465
#> ... Procrustes: rmse 0.002052298 max resid 0.0142497
#> Run 5 stress 0.0004445717
#> ... Procrustes: rmse 0.006812898 max resid 0.02809961
#> Run 6 stress 0.0004523721
#> ... Procrustes: rmse 0.005890348 max resid 0.02803158
#> Run 7 stress 0.0005441538
#> ... Procrustes: rmse 0.001712747 max resid 0.01348821
#> Run 8 stress 0.0007116719
#> ... Procrustes: rmse 0.002390954 max resid 0.01391582
#> Run 9 stress 0.0004893539
#> ... Procrustes: rmse 0.001006341 max resid 0.004151976
#> ... Similar to previous best
#> Run 10 stress 0.0006132705
#> ... Procrustes: rmse 0.001437817 max resid 0.009497169
#> ... Similar to previous best
#> Run 11 stress 0.0005200162
#> ... Procrustes: rmse 0.001915949 max resid 0.01379101
#> Run 12 stress 0.0004972366
#> ... Procrustes: rmse 0.005009449 max resid 0.02466239
#> Run 13 stress 0.0007081643
#> ... Procrustes: rmse 0.00246024 max resid 0.007056748
#> ... Similar to previous best
#> Run 14 stress 0.0003894657
#> ... Procrustes: rmse 0.009047779 max resid 0.0407539
#> Run 15 stress 0.000550324
#> ... Procrustes: rmse 0.001366108 max resid 0.006962215
#> ... Similar to previous best
#> Run 16 stress 0.0006636296
#> ... Procrustes: rmse 0.004983043 max resid 0.02235771
#> Run 17 stress 0.00049826
#> ... Procrustes: rmse 0.00131955 max resid 0.006940758
#> ... Similar to previous best
#> Run 18 stress 0.0005296897
#> ... Procrustes: rmse 0.001130324 max resid 0.006652075
#> ... Similar to previous best
#> Run 19 stress 0.0006853578
#> ... Procrustes: rmse 0.002186779 max resid 0.009262767
#> ... Similar to previous best
#> Run 20 stress 0.0005200306
#> ... Procrustes: rmse 0.00118174 max resid 0.008870081
#> ... Similar to previous best
#> *** Best solution repeated 10 times