1 통계학
통계학은 데이터를 수집, 분석, 해석하고 결과를 도출하는 과학으로, 현실 세계의 불확실성을 다루는 데 필수적인 도구다. 통계학은 크게 기술통계학과 추론통계학으로 나뉘며, 데이터 수집 및 처리, 확률 모형, 다변량 분석 등 다양한 분야를 망라하고 있다.
1.1 전체적인 흐름
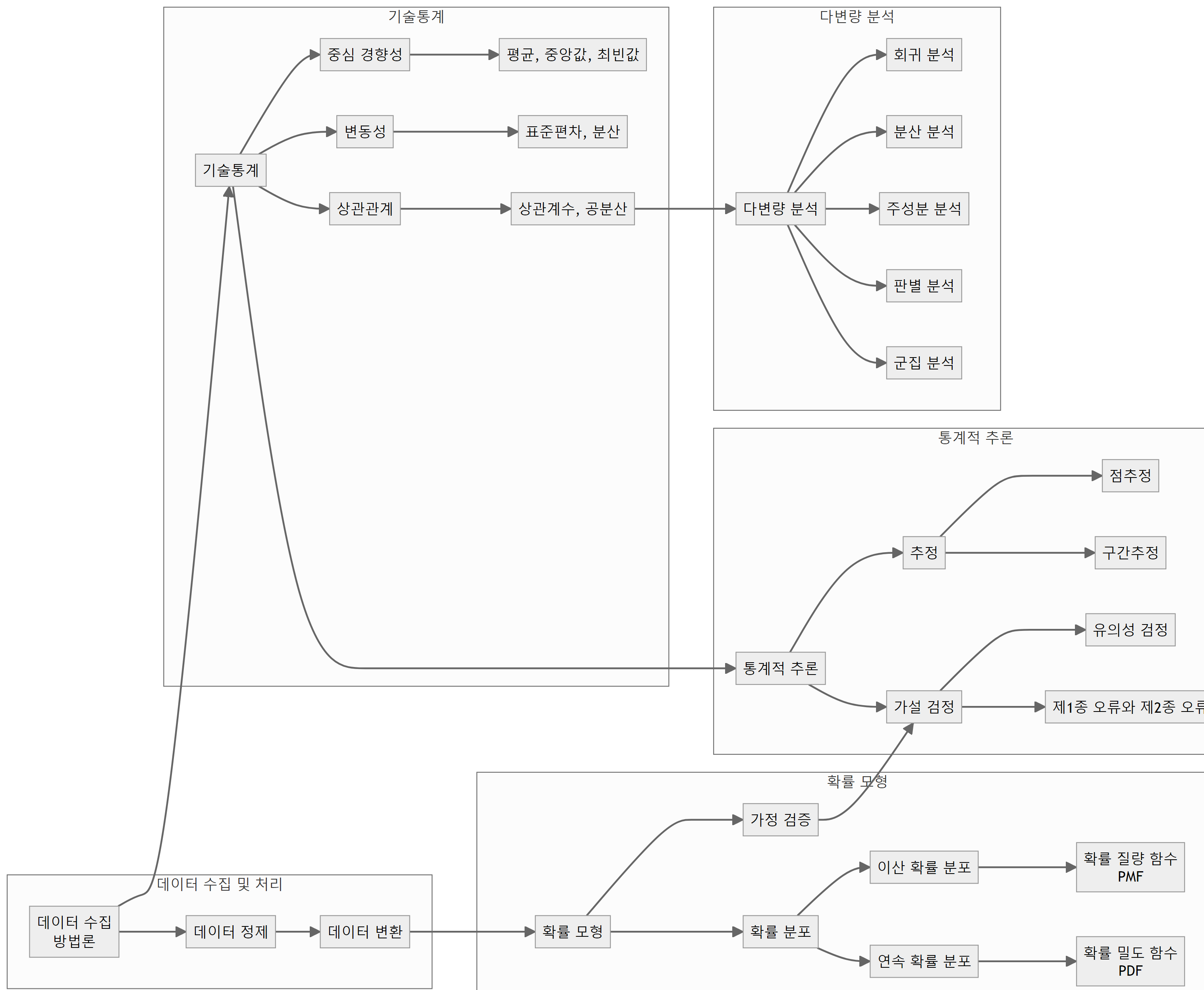
통계학의 출발점은 데이터 수집 및 처리다. 데이터 수집 방법론에는 표본추출, 실험설계, 관측 등이 포함되며, 수집된 데이터는 정제와 변환 과정을 거쳐 분석에 적합한 형태로 가공된다.
기술통계학은 수집된 데이터를 요약, 시각화하고 주요 특징을 파악하는 데 초점을 맞춘다. 중심 경향성, 변동성, 상관관계 등의 개념을 통해 데이터의 분포와 변수 간 관계를 이해할 수 있다. 평균, 중앙값, 최빈값은 중심 경향성을 나타내는 대표적인 측도이며, 표준편차와 분산은 데이터의 변동성을 측정한다. 상관계수와 공분산은 변수 간의 선형 관계를 파악하는 데 사용된다.
확률 모형은 데이터의 불확실성을 수학적으로 표현하는 데 활용된다. 확률 분포는 이산 확률 분포와 연속 확률 분포로 나뉘며, 각각 확률 질량 함수(PMF)와 확률 밀도 함수(PDF)로 표현된다. 확률 모형의 적합성을 평가하기 위해 가정 검증이 수행된다.
추론통계학은 표본 데이터를 바탕으로 모집단의 특성을 추론하는 데 주력한다. 추정은 모수의 값을 점추정 또는 구간추정을 통해 예측하는 과정이다. 가설 검정은 통계적 가설의 타당성을 판단하기 위해 유의성 검정을 수행하며, 이 과정에서 제1종 오류와 제2종 오류를 고려한다.
다변량 분석은 여러 변수 간의 복잡한 관계를 탐구하는 데 사용된다. 회귀 분석은 독립변수와 종속변수 간의 관계를 모형화하며, 분산 분석은 집단 간 평균 차이를 검정한다. 주성분 분석, 판별 분석, 군집 분석 등은 고차원 데이터의 차원 축소와 패턴 인식에 활용된다.
1.2 데이터 과학
통계학과 데이터 과학은 불가분의 관계에 있다. 현대 데이터 과학은 통계학 기본 원칙과 방법론에 기반하여 발전해왔다. 통계학이 불확실성을 다루고 예측 가능한 패턴을 도출하기 위해 데이터 수집, 정제, 분석, 해석에 주력하듯이, 데이터 과학 역시 이러한 원칙을 바탕으로 더욱 광범위하고 다양한 데이터로부터 인사이트를 이끌어낸다.
데이터 과학은 통계학의 추론, 가설 검정, 회귀 모형 등의 개념을 핵심 도구로 활용한다. 다변량 분석, 예측 모형, 기계 학습 알고리즘 등 데이터 과학의 주요 기법들은 통계학적 원리에 기반하여 복잡한 데이터 패턴을 추출하고 예측한다. 이를 통해 데이터로부터 심층적인 인사이트를 얻고, 이를 바탕으로 의사결정을 지원하며 전략을 수립하는 데 기여한다.
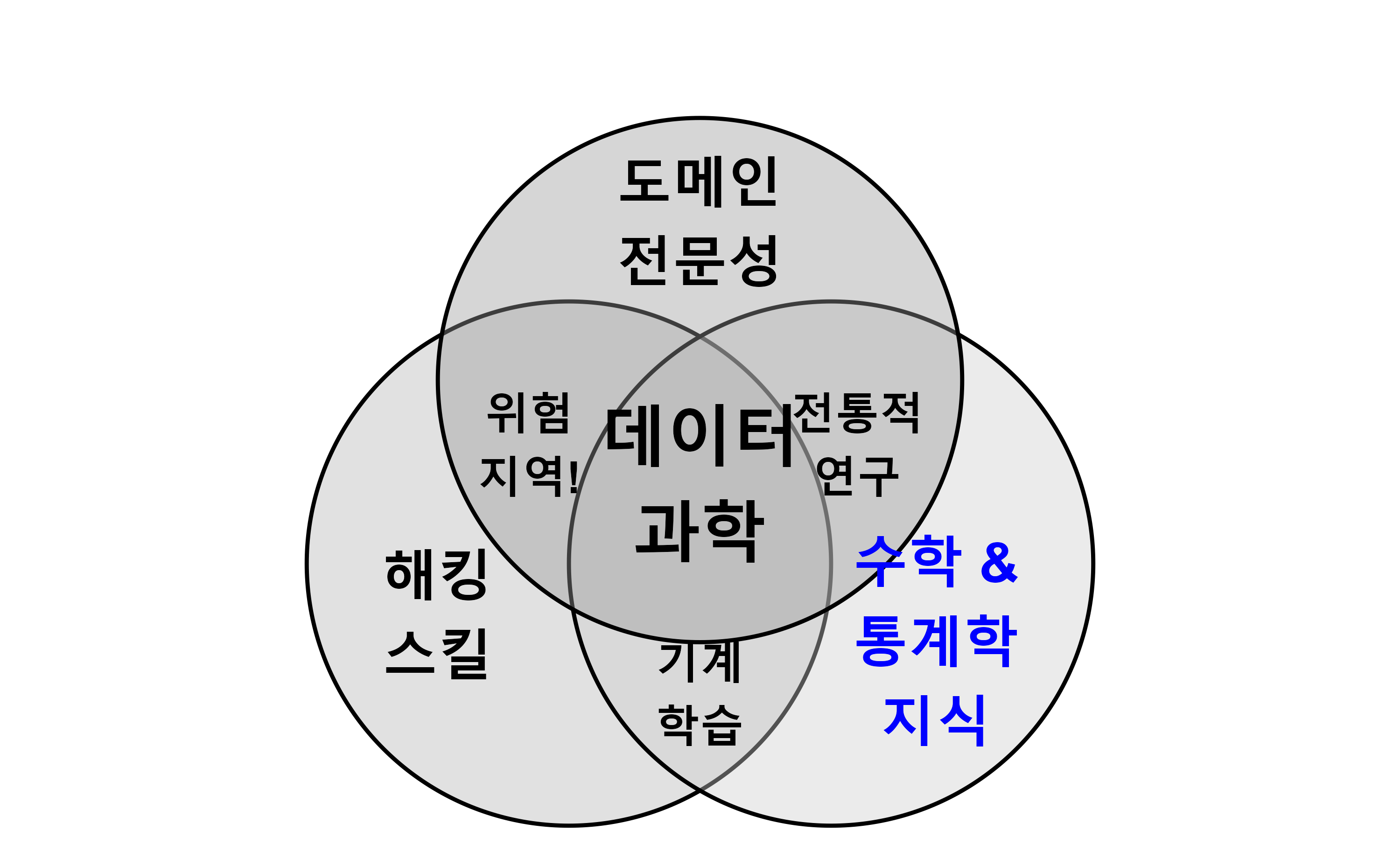
콘웨이 그림 1.2 에서 볼 수 있듯이, 진정한 데이터 과학은 해킹 스킬, 통계학 지식, 도메인 전문성이 교차하는 지점에서 탄생한다. 데이터 과학자는 통계학과 컴퓨터 과학의 경계를 넘나들며, 다양한 분야의 지식을 융합하여 현실 세계의 문제를 해결한다. 통계학 지식은 필수불가결하지만 그것만으로는 부족하고, 창의적 사고, 도메인 전문성, 소프트웨어 개발 능력 등 다방면의 역량이 갖춰질 때 비로소 진정한 데이터 과학자로 성장할 수 있다.
콘웨이 데이터 과학 벤 다이어그램은 데이터 과학자에게 필요한 역량을 해킹 스킬, 수학 및 통계학 지식, 도메인 전문성이라는 세 가지 영역으로 시각적으로 표현하여 단순히 기술적 역량만으로는 진정한 데이터 과학자가 될 수 없음을 강조한다. 해당 분야에 대한 전문 지식과 수학/통계학적 사고력이 뒷받침되어야 비로소 데이터 과학자로서의 역량을 갖출 수 있다.
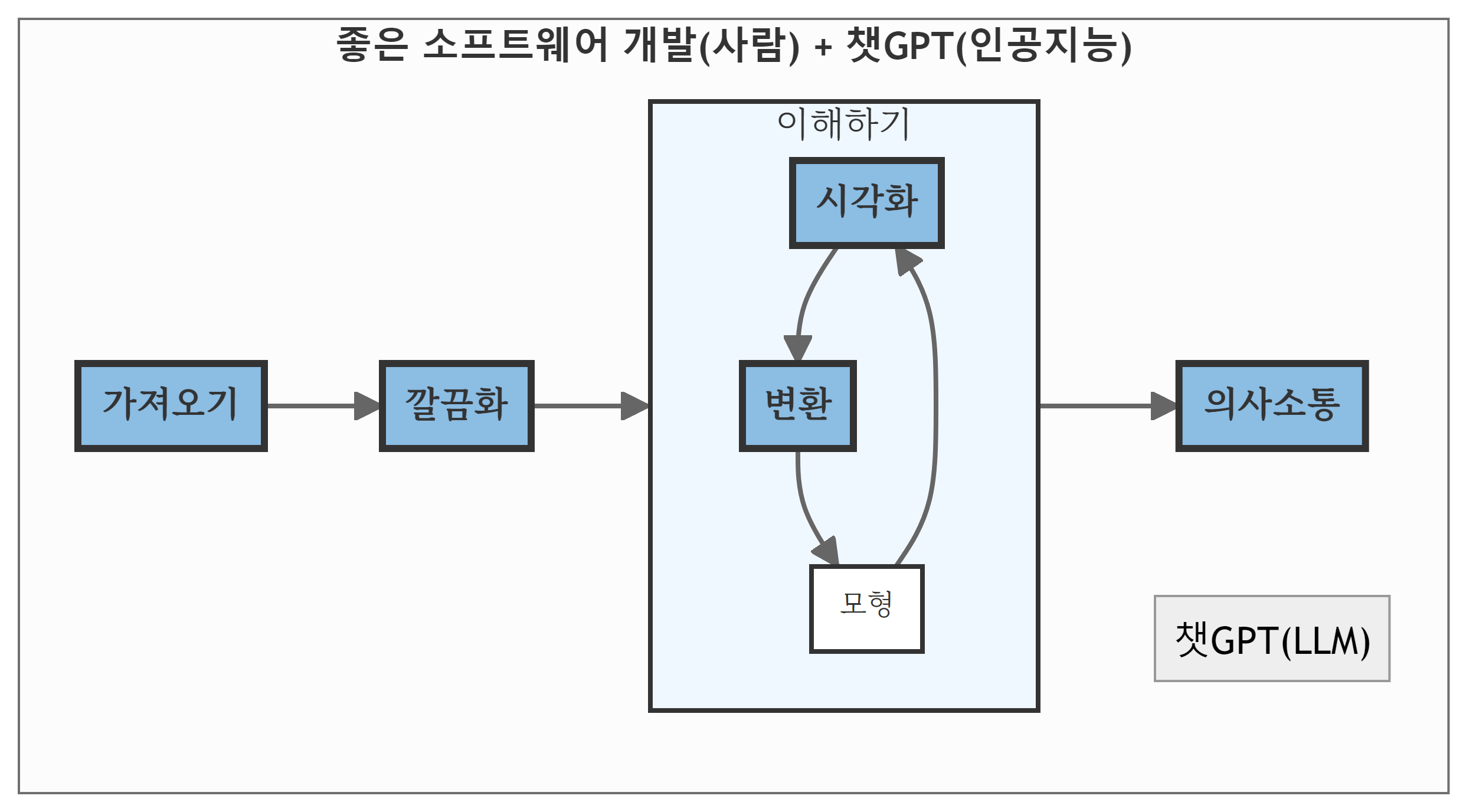
통계학을 각 부분별로 나눠서 상세히 살펴보는 대신 데이터 과학을 구성하는 데이터 가져오기(Import), 깔끔화(Tidy), 변환(Transform), 시각화(visualize)에 대해 전체적인 작업흐름을 신속히 일별하고 시작하는 것이 최근의 추세다. 통계 이론을 적용하여 다양한 데이터에 대한 이해와 분석 경험이 쌓이면서 tidyverse가 새롭게 출현했고, 관련하여 데이터 문법(grammar of data), 그래프 문법(grammar of graphics), 표 문법(grammar of table)이 체계화 되면서 tidyverse의 중추를 이루게 되었다.
남극 팔머 군도에서 수집된 펭귄 데이터셋은 통계학에 뿌리를 둔 데이터 과학 전체적인 흐름을 이해하는 데 있어 훌륭한 예시가 될 수 있다. 펭귄 데이터셋은 아델리, 턱끈, 젠투 펭귄 3종에 대한 다양한 신체 측정값을 포함하고 있어, 연구자들은 펭귄의 생물학적 특성과 환경 간의 상호작용을 연구할 수 있다. 통계학과 데이터 과학의 기본 원리를 적용하여 펭귄 데이터로부터 의미 있는 정보를 추출하고, 이를 바탕으로 생태학적 인사이트를 도출하는 과정은 매우 흥미로운 과정이다.