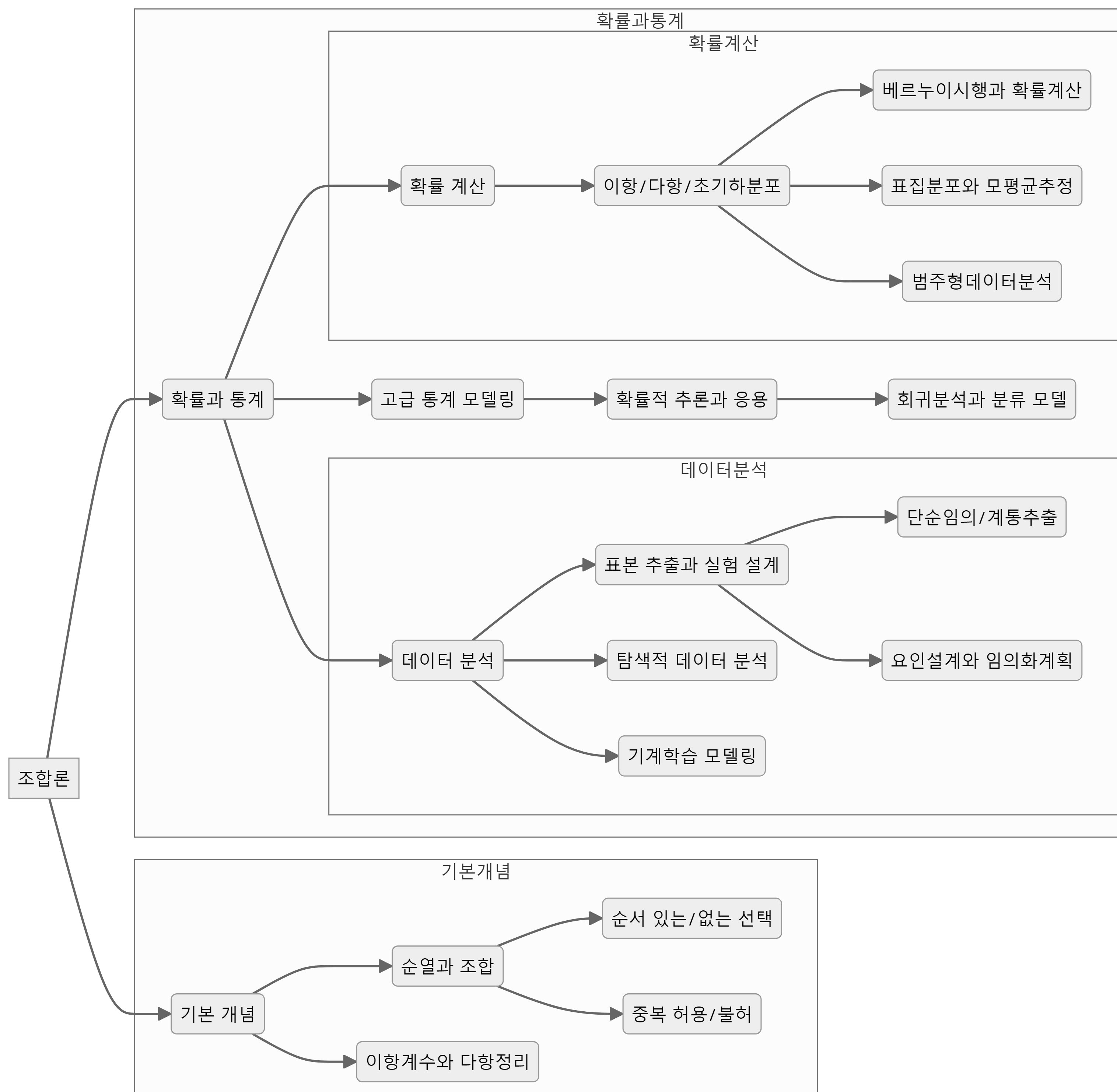
20 조합론
조합론은 수학의 한 분야로 알려져 있으며, 다양한 수학적, 과학적, 공학적 문제 해결에 광범위하게 활용된다. 조합론은 선택과 배열의 문제를 다루며, 특히 확률과 통계학에서 핵심적인 역할을 한다. 조합론은 가능한 모든 경우의 수를 체계적으로 계산함으로써 복잡한 문제 상황에서 예상 가능한 결과의 범위를 정의하고, 그 결과가 발생할 확률을 예측하는 데 필수적이다.
조합론은 통계학과 밀접한 관계를 가지며, 통계학적 문제 해결에 필수적인 도구로 활용된다. 조합론은 확률 계산의 기초를 제공하고, 통계적 실험 설계, 통계 모형, 데이터 분석 및 통계적 추론에 깊이 관여한다.
예를 들어, 확률 계산에서 조합론은 특정 결과의 가능성을 계산을 통해 확률론적 모형과 추론의 기반을 제공한다. 실험 설계에서는 조합론을 활용하여 표본 추출 방법과 실험 배열을 최적화하여 데이터의 대표성을 확보하고 편향을 줄이는 데 기여한다.
20.1 수학적 정의
20.1.1 순열
순열은 서로 다른 n개의 원소 중에서 r개를 선택하여 일렬로 나열하는 것을 말한다. 수학적으로 순열의 수는 다음 공식으로 계산된다:
\[ nPr = \frac{n!}{(n-r)!} \]
여기서 \(n!\)은 n의 팩토리얼을 의미하며, \((n-r)!\)은 선택되지 않은 나머지 요소들의 팩토리얼이다.
20.1.2 조합
조합은 순서를 고려하지 않고 n개의 원소 중에서 r개를 선택하는 경우의 수를 말한다. 조합의 수는 다음 공식으로 주어진다:
\[ nCr = \frac{n!}{r!(n-r)!} \]
이 공식은 n개의 항목 중 r개를 선택할 때 순서를 고려하지 않는다는 점을 반영한다.
20.1.3 이항계수와 다항정리
이항계수는 조합 공식과 밀접하게 관련되어 있으며, \((x+y)^n\)을 전개할 때 각 항의 계수를 결정한다. 다항정리는 이항정리를 확장하여 여러 변수의 합의 거듭제곱을 전개하는 데 사용된다.
20.2 복잡한 순열/조합 문제
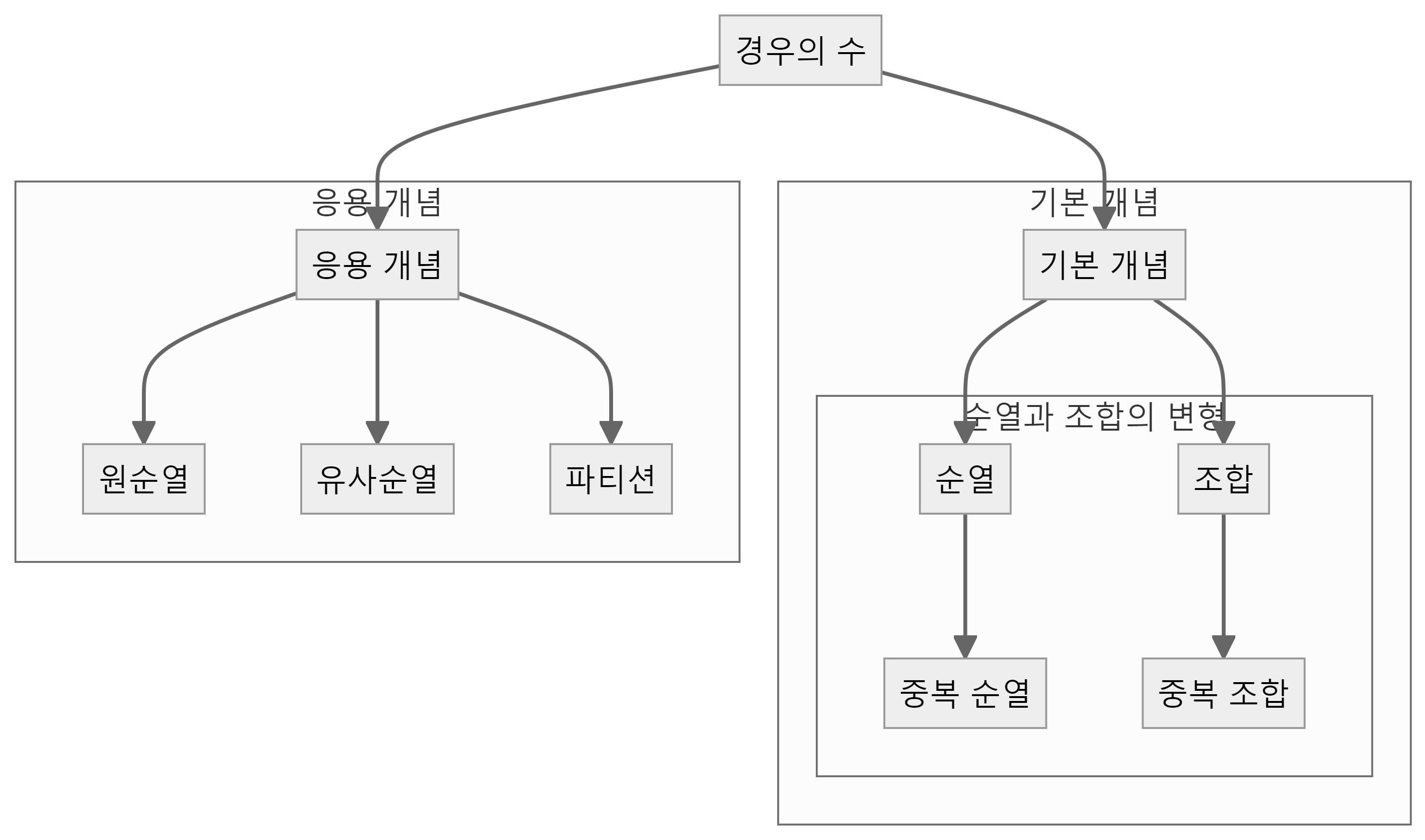
복잡한 순열 및 조합 문제에는 중복 순열, 중복 조합, 원 순열, 파티션 문제 등이 포함된다. 이러한 문제들은 실제 생활에서 자주 발생하는 다양한 상황을 모델링하는 데 유용하다.
조합론은 이와 같이 다양한 분야에서 광범위하게 응용되며, 복잡한 문제의 해결을
위해 필수적인 도구로 활용된다. 조합론을 통해 얻은 이해는 실제 환경에서의 의사결정 과정을 보다 명확하고 효율적으로 만든다.
20.3 순열과 조합
순열 (Permutation): n개의 요소 중에서 r개를 선택하여 순서를 고려하여 나열하는 경우의 수입니다. 순열의 개수는 다음과 같이 계산됩니다: \(P(n, r) = \frac{n!}{(n-r)!} = n \times (n-1) \times \cdots \times (n-r+1)\)
조합 (Combination): n개의 요소 중에서 r개를 선택하는 경우의 수로, 순서를 고려하지 않습니다. 조합의 개수는 다음과 같이 계산됩니다: \(C(n, r) = \binom{n}{r} = \frac{n!}{r!(n-r)!} = \frac{P(n, r)}{r!}\)
중복 순열 (Permutation with Repetition): n개의 요소 중에서 r개를 선택하여 순서를 고려하여 나열하는 경우의 수로, 같은 요소를 여러 번 선택할 수 있습니다. 중복 순열의 개수는 다음과 같이 계산됩니다: \({}_{n}Π_{r} = n^r\)
중복 조합 (Combination with Repetition): n개의 요소 중에서 r개를 선택하는 경우의 수로, 같은 요소를 여러 번 선택할 수 있으며 순서를 고려하지 않습니다. 중복 조합의 개수는 다음과 같이 계산됩니다: \(\binom{n+r-1}{r} = \frac{(n+r-1)!}{r!(n-1)!}\)
응용 개념: 1. 원순열 (Circular Permutation): n개의 요소를 원형으로 배열하는 경우의 수입니다. 원순열의 개수는 \((n-1)!\)로 계산됩니다.
유사순열 (Derangement): n개의 요소를 배열할 때, 모든 요소가 원래의 위치에 있지 않도록 하는 경우의 수입니다. 유사순열의 개수는 다음과 같이 근사적으로 계산됩니다: \(!n \approx \lfloor \frac{n!}{e} + \frac{1}{2} \rfloor\)
파티션 (Partition): 양의 정수 n을 더해서 n이 되는 경우의 수입니다. 파티션의 개수는 파티션 함수 \(p(n)\)으로 나타내며, 일반적인 공식은 알려져 있지 않습니다.
순열과 조합은 기본적인 경우의 수 계산 방법으로, 중복 순열과 중복 조합은 이를 확장한 개념이다. 원순열은 순열의 특수한 경우이고, 유사순열은 순열에서 모든 요소가 원래 위치에 있지 않은 경우를 다루고 파티션은 순열, 조합과는 별개의 개념으로 정수의 분할을 다룬다.
20.4 순열 코드
20.4.1 R 코드
무지개 색깔 7개로 만들 수 있는 순열의 경우의 수를 계산해보자. 무지개 색깔은 빨강, 주황, 노랑, 초록, 파랑, 남색, 보라로 가정한다.
- \(n\) = 7 (무지개 색깔의 개수)
- \(r\) = 7 (뽑는 색깔의 개수, 순서대로 모두 뽑는 경우)
순열의 경우의 수는 \(_{n}P_{r}\)로 표기하며, 수식으로 다음과 같이 풀 수 있다. \(n!\)은 \(n\)의 계승(factorial)을 의미하며, \(n\)부터 1까지의 모든 자연수를 곱한 값이다.
\[_{n}P_{r} = \frac{n!}{(n-r)!}\]
따라서, 무지개 색깔 7개로 만들 수 있는 순열의 경우의 수는
\[_{7}P_{7} = \frac{7!}{(7-7)!} = \frac{7!}{0!} = 7! = 7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1 = 5,040\]
무지개 색깔 7개를 순서대로 배열하는 경우의 수는 5,040가지다.
20.4.2 shiny 앱
#| label: shinylive-permutation-rainbow
#| viewerHeight: 600
#| standalone: true
library(shiny)
library(combinat)
ui <- fluidPage(
titlePanel("무지개 색깔 순열"),
sidebarLayout(
sidebarPanel(
h3("설명"),
p("무지개 색깔 중 원하는 색깔을 선택하여 해당 색깔들의 순열을 생성하고 출력합니다."),
p("색깔을 선택한 후 '순열 생성' 버튼을 클릭하면 선택한 색깔들의 모든 가능한 순서가 테이블 형태로 출력됩니다."),
p("또한, 선택한 색깔의 개수에 따른 전체 순열의 개수가 수식으로 표현되어 출력됩니다."),
uiOutput("total_permutations"),
br(),
checkboxGroupInput("selected_colors", "색깔 선택:",
choices = c("빨강" = "빨강", "주황" = "주황", "노랑" = "노랑", "초록" = "초록",
"파랑" = "파랑", "남색" = "남색", "보라" = "보라"),
selected = c("빨강", "주황", "노랑", "초록", "파랑", "남색", "보라"),
inline = TRUE),
actionButton("generate", "순열 생성")
),
mainPanel(
tableOutput("permutations")
)
)
)
server <- function(input, output) {
permutations <- eventReactive(input$generate, {
color_list <- combinat::permn(input$selected_colors)
color_matrix <- do.call(rbind, color_list)
color_df <- as.data.frame(color_matrix)
colnames(color_df) <- paste0("색깔", 1:length(input$selected_colors))
color_df <- cbind(순번 = 1:nrow(color_df), color_df)
color_df
})
output$permutations <- renderTable({
permutations()
}, rownames = FALSE)
output$total_permutations <- renderUI({
num_colors <- length(input$selected_colors)
total <- factorial(num_colors)
latex_code <- paste0("$$_{", num_colors, "}P_{", num_colors, "} = \\frac{", num_colors, "!}{(", num_colors, "-", num_colors, ")!} = ", num_colors, "! = ", total, "$$")
withMathJax(
helpText("전체 색상 순열 개수:"),
helpText(latex_code)
)
})
}
shinyApp(ui, server)
20.5 조합 코드
20.5.1 R 코드
한식 뷔페에는 불고기, 비빔밥, 갈비찜, 된장찌개, 김치찌개, 잡채, 떡볶이 총 7가지 메뉴가 있다. 이 중 3가지 메뉴를 선택하여 점심 식사를 하려고 한다. 가능한 모든 조합의 수는 다음과 같이 계산할 수 있다.
\(\binom{7}{3} = \frac{7!}{3!(7-3)!} = \frac{7!}{3!4!} = 35\)
따라서 7가지 메뉴 중 3가지를 선택하는 경우의 수는 35가지이다.
정상적인 동작을 위해 7개 메뉴 중 하나를 뽑는 경우의 수를 출력하여 확인한다. combn() 함수를 사용하여 7가지 메뉴 중 3개를 선택하는 모든 조합을 생성하고, choose() 함수를 사용하여 조합의 수를 계산한다. 코드를 실행하면 선택 가능한 모든 조합과 조합의 수가 출력된다.
20.5.2 shiny 앱
#| label: shinylive-combination-korean-menu
#| viewerHeight: 600
#| standalone: true
library(shiny)
ui <- fluidPage(
titlePanel("한식 메뉴 조합 계산기"),
sidebarLayout(
sidebarPanel(
h3("설명"),
p("한식 뷔페에서 제공하는 메뉴 중 원하는 메뉴를 선택하여 가능한 조합을 생성하고 출력합니다."),
p("메뉴를 선택한 후 '조합 생성' 버튼을 클릭하면 선택한 메뉴의 모든 가능한 조합이 테이블 형태로 출력됩니다."),
p("또한, 선택한 메뉴의 개수에 따른 전체 조합의 수가 수식으로 표현되어 출력됩니다."),
uiOutput("total_combinations"),
br(),
checkboxGroupInput("selected_menu", "메뉴 선택:",
choices = c("불고기", "비빔밥", "갈비찜", "된장찌개",
"김치찌개", "잡채", "떡볶이"),
selected = c("불고기", "비빔밥", "갈비찜"),
inline = TRUE),
numericInput("num_select", "선택할 메뉴 수:", value = 3, min = 1, max = 7),
actionButton("generate", "조합 생성")
),
mainPanel(
tableOutput("combinations")
)
)
)
server <- function(input, output) {
combinations <- eventReactive(input$generate, {
menu_combinations <- combn(input$selected_menu, input$num_select)
menu_combinations_df <- t(menu_combinations)
colnames(menu_combinations_df) <- paste0("조합", 1:ncol(menu_combinations_df))
menu_combinations_df <- cbind(순번 = 1:nrow(menu_combinations_df), menu_combinations_df)
menu_combinations_df
})
output$combinations <- renderTable({
combinations()
}, rownames = FALSE)
output$total_combinations <- renderUI({
n <- length(input$selected_menu)
r <- input$num_select
total <- choose(n, r)
latex_code <- paste0("$$\\binom{", n, "}{", r, "} = \\frac{", n, "!}{", r, "!(", n, "-", r, ")!} = ", total, "$$")
withMathJax(
helpText("전체 조합의 수:"),
helpText(latex_code)
)
})
}
shinyApp(ui, server)
20.6 중복순열
자동차 번호판은 보통 문자 1자리와 숫자 4자리의 조합으로 이루어진다. 번호판의 첫 자리에는 문자(가, 나, 다, 라, 마, 바, 사, 아, 자, 차, 카, 타, 파, 하) 중 하나를 사용하고, 나머지 4자리에는 숫자(0-9)를 사용한다고 가정한다. 가능한 모든 번호판의 조합을 중복순열 경우의 수를 활용하여 계산할 수 있다. 문자는 14개(가, 나, 다, 라, 마, 바, 사, 아, 자, 차, 카, 타, 파, 하)가 있고, 숫자는 0부터 9까지 10개가 있다. 문자는 첫 자리에만 사용되므로 14가지 경우의 수가 있고, 숫자는 나머지 4자리에 사용되므로 \(10^4 = 10,000\)가지 경우의 수가 있다. 따라서 가능한 번호판의 총 개수는 다음과 같이 계산할 수 있다:
\[14 \times 10^4 = 140,000\]
즉, 가능한 번호판의 조합은 총 140,000가지이다.
20.7 중복조합
중복조합은 \(n\)개 원소 중에서 \(r\)개를 선택할 때, 같은 원소를 여러 번 선택할 수 있는 경우를 말한다. 이때 선택한 원소의 순서는 고려하지 않는다. 즉, (1, 2, 2)와 (2, 1, 2)는 같은 중복조합으로 간주한다.
예를 들어, 아이스크림 가게에서 바닐라, 초콜릿, 딸기 3가지 맛의 아이스크림이 있고, 2가지 맛을 선택하여 주문할 수 있다고 가정해보자. 이때 같은 맛을 2번 선택할 수도 있다. 중복조합을 활용하여 가능한 모든 아이스크림 주문의 조합을 계산할 수 있다.
중복조합의 개수는 다음과 같은 공식으로 계산할 수 있다. \(n\)은 전체 원소의 개수, \(r\)은 선택하는 원소의 개수다.
\[\binom{n+r-1}{r} = \frac{(n+r-1)!}{r!(n-1)!}\]
위의 아이스크림 주문 예시에서 \(n=3\) (아이스크림 맛의 개수), \(r=2\) (선택하는 맛의 개수)이므로, 중복조합의 개수는 다음과 같이 계산된다.
\[\binom{3+2-1}{2} = \binom{4}{2} = \frac{4!}{2!(4-2)!} = \frac{4 \times 3}{2 \times 1} = 6\]
즉, 아이스크림 2가지 맛을 선택하는 경우의 수는 중복을 허용할 때 총 6가지이다.
20.8 원순열
원순열은 원형 구조를 가진 배열 문제에서 유용하게 활용될 수 있다. 5명의 사람(A, B, C, D, E)이 원탁에 앉는 경우를 생각해보면, 시계 방향이나 반시계 방향으로 회전해도 같은 배치로 간주한다. 즉, (A, B, C, D, E)로 앉는 것과 (B, C, D, E, A), (C, D, E, A, B) 등은 모두 같은 배치이다.
5명이 원탁에 앉는 경우, 가능한 배치의 수는 원순열의 개수와 같고, 이는 \((5-1)! = 4! = 24\)가지가 된다.
원순열의 개수가 \((n-1)!\)로 계산되는 이유는 다음과 같다. 첫 번째 사람의 자리를 기준으로 잡으면, 나머지 \((n-1)\)명의 사람들을 배치하는 경우의 수는 \((n-1)!\)가 된다. 첫 번째 사람의 자리는 고정되어 있다고 가정하므로, 원탁에서의 위치가 변해도 같은 배치로 간주되기 때문이다.
R 코드로 5명의 원탁 배치 문제를 구현해보면 다음과 같다.
#> 사람: A B C D E
#> 가능한 원탁 배치의 수: 24
#> 좌석1 좌석2 좌석3 좌석4 좌석5
#> [1,] "B" "C" "D" "E" "A"
#> [2,] "C" "D" "E" "A" "B"
#> [3,] "D" "E" "A" "B" "C"
#> [4,] "E" "A" "B" "C" "D"
#> [5,] "C" "D" "E" "A" "B"
#> [6,] "B" "C" "D" "E" "A"
#> [7,] "C" "D" "E" "A" "B"
#> [8,] "D" "E" "A" "B" "C"
#> [9,] "E" "A" "B" "C" "D"
#> [10,] "C" "D" "E" "A" "B"
#> [11,] "B" "C" "D" "E" "A"
#> [12,] "C" "D" "E" "A" "B"
#> [13,] "D" "E" "A" "B" "C"
#> [14,] "E" "A" "B" "C" "D"
#> [15,] "C" "D" "E" "A" "B"
#> [16,] "B" "C" "D" "E" "A"
#> [17,] "C" "D" "E" "A" "B"
#> [18,] "D" "E" "A" "B" "C"
#> [19,] "E" "A" "B" "C" "D"
#> [20,] "C" "D" "E" "A" "B"
#> [21,] "B" "C" "D" "E" "A"
#> [22,] "C" "D" "E" "A" "B"
#> [23,] "D" "E" "A" "B" "C"
#> [24,] "E" "A" "B" "C" "D"20.9 유사순열
학생 A, B, C와 감독관 1, 2, 3이 있다고 가정해봅시다. 각 학생은 자신과 동일한 번호의 감독관에게 감독받지 않도록 자리를 배치해야 합니다.
먼저, 유사순열의 개수를 수식으로 계산하는 방법을 살펴보겠습니다. 유사순열의 개수는 다음과 같은 공식으로 계산할 수 있습니다:
\[!n = n! \sum_{i=0}^{n} \frac{(-1)^i}{i!}\]
여기서 \(!n\)은 \(n\)개의 원소에 대한 유사순열의 개수를 나타냅니다.
\(n = 3\)인 경우, 유사순열의 개수는 다음과 같이 계산할 수 있습니다:
\[!3 = 3! \left(\frac{(-1)^0}{0!} + \frac{(-1)^1}{1!} + \frac{(-1)^2}{2!} + \frac{(-1)^3}{3!}\right)\]
\(= 6 \left(1 - 1 + \frac{1}{2} - \frac{1}{6}\right)\)
\(= 6 \cdot \frac{1}{3} = 2\)
따라서 3명의 학생과 3명의 감독관에 대한 유사순열의 개수는 2입니다.
이제 R 코드로 유사순열을 생성하고 결과를 출력해보겠습니다.
#> 학생: A B C
#> 감독관: 1 2 3
#> 가능한 시험 감독 배치 수: 2
#> 가능한 시험 감독 배치:
#> 배치 1 : C A B
#> 배치 2 : B C A20.10 파티션
파티션은 조합론의 중요한 개념 중 하나로, 수학적 문제 해결과 알고리즘 개발에 활용된다. 파티션은 자연수 \(n\)을 더해서 \(n\)이 되는 경우의 수를 의미한다. 즉, 양의 정수 \(n\)을 합이 \(n\)이 되도록 더할 수 있는 방법의 수를 나타낸다.
파티션 함수 \(p(n)\)은 자연수 \(n\)의 파티션 개수를 계산하는 함수이다. 이 함수는 다음과 같은 점화식으로 정의된다:
\[ \begin{align*} p(0) &= 1 \\ p(n) &= p(n-1) + p(n-2) - p(n-5) - p(n-7) + p(n-12) + p(n-15) - \cdots \end{align*} \]
파티션 함수는 오일러(Euler)의 파티션 항등식으로도 표현될 수 있다.
\[ \sum_{n=0}^{\infty} p(n)x^n = \prod_{k=1}^{\infty} \frac{1}{1-x^k} \]
파티션은 다양한 문제 상황에서 활용될 수 있다. 예를 들어, 자연수를 분할하는 방법을 나타내는 문제, 동전 교환 문제, 자원 할당 문제 등에서 파티션이 사용될 수 있다.
다음은 3종류 동전(1원, 5원, 10원)으로 10원을 만드는 파티션을 생성하는 R 코드다. 주어진 동전 종류를 사용하여 특정 금액의 모든 파티션을 생성하고, 중복을 제거하여 고유한 파티션만 출력한다. 주어진 금액(10원)을 동전으로 표현하는 다양한 방법을 확인할 수 있다.
#> 파티션의 개수: 4
#> 파티션:
#> 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1
#> 1 + 1 + 1 + 1 + 1 + 5
#> 5 + 5
#> 10주어진 동전의 종류가 1원, 5원, 10원이므로 각 동전의 개수를 나타내는 변수를 \(x_1, x_2, x_3\)로 정의하면 정수 집합(\(\mathbb{Z}\))에서 다음과 같은 방정식을 세울 수 있다.
\[ \begin{align*} x_1 + 5x_2 + 10x_3 &= 10 \\ x_1, x_2, x_3 &\geq 0 \\ x_1, x_2, x_3 &\in \mathbb{Z} \end{align*} \]
위 방정식은 1원짜리 동전의 개수 \(x_1\), 5원짜리 동전의 개수 \(x_2\), 10원짜리 동전의 개수 \(x_3\)를 나타낸다. 상기 조건을 만족하는 변수들의 값을 찾아야 한다. 문제를 해결하기 위해 생성함수(generating function)를 사용할 수 있다. 생성함수는 다항식의 계수를 이용하여 문제를 해결하는 방법으로, 조합론과 관련된 다양한 수학적 도구와 연결된다.
\[ G(x) = (1 + x + x^2 + \cdots)(1 + x^5)(1 + x^{10}) \]
이 생성함수를 전개하면 \(x^{10}\)의 계수가 10원을 만들 수 있는 동전 조합의 개수를 나타낸다. 생성함수를 전개하면 다음과 같다:
\[ G(x) = 1 + x + x^2 + x^3 + x^4 + 2x^5 + x^6 + x^7 + x^8 + x^9 + 4x^{10} + \cdots \]
따라서, \(x^{10}\)의 계수인 4가 10원을 만들 수 있는 동전 조합의 개수이다. 계산량이 많아 R 코드로 작성하면 쉽게 구할 수 있다. 코드에서 coefficient() 함수는 재귀적으로 생성함수의 계수를 계산한다. 주어진 금액 amount와 동전 종류 coins를 입력으로 받아 해당 금액을 만들 수 있는 동전 조합의 개수를 반환한다. 따라서, 1원, 5원, 10원 동전으로 10원을 만드는 문제는 생성함수를 사용하여 해결할 수 있으며, 10원을 만들 수 있는 동전 조합의 개수는 4가지다.
#> 10원을 만들 수 있는 동전 조합의 개수: 4