24 연속형 확률분포
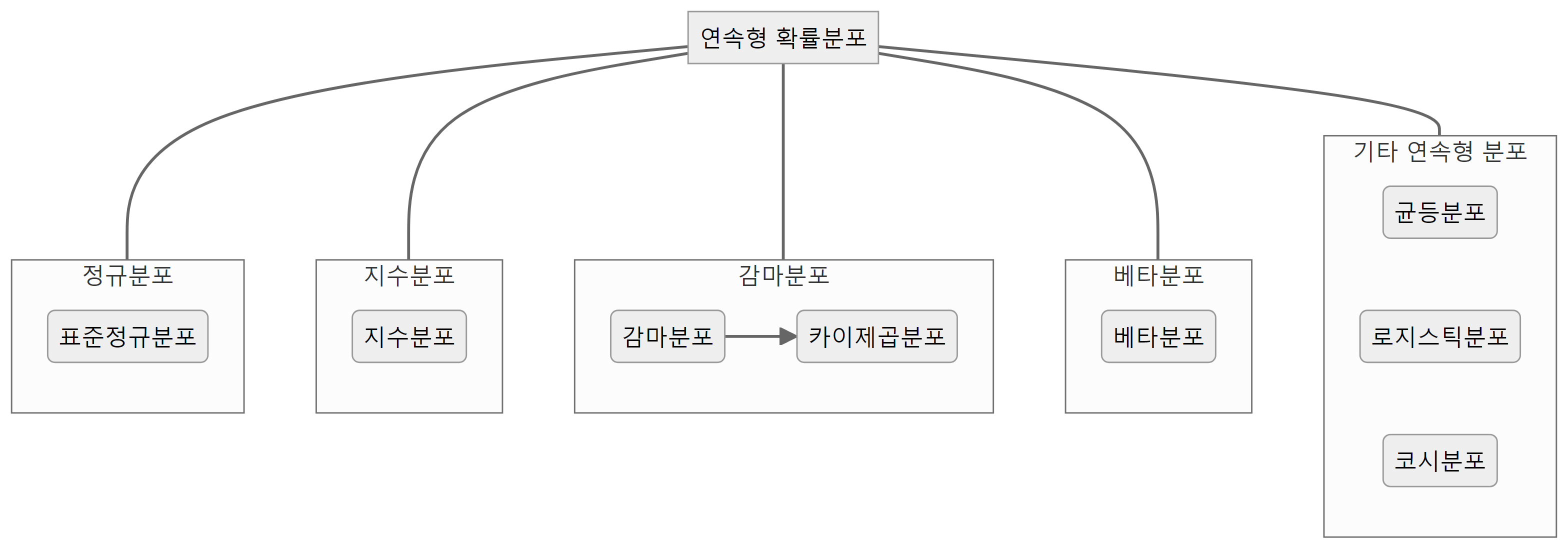
연속형 확률분포(continuous probability distribution)는 확률변수가 연속적인 값을 가지는 경우의 확률분포를 말한다. 연속형 확률분포의 대표적인 예로는 정규분포, 지수분포, 감마분포 등이 있다.
24.1 정규분포
정규분포(normal distribution)는 가장 널리 사용되는 연속형 확률분포 중 하나로, 실제 세계의 많은 현상을 잘 설명할 수 있다. 정규분포는 평균 \(\mu\)와 분산 \(\sigma^2\)의 두 모수로 특징지어진다.
확률변수 \(X\)가 정규분포를 따른다면, 이를 \(X \sim N(\mu, \sigma^2)\)로 표기하고 확률밀도함수(PDF)는 다음과 같다.
\[f(x) = \frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{(x-\mu)^2}{2\sigma^2}} \qquad -\infty < x < \infty\]
정규분포의 누적분포함수(CDF)는 다음과 같이 정의된다.
\[F(x) = P(X \leq x) = \int_{-\infty}^x \frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{(t-\mu)^2}{2\sigma^2}} dt\]
적분은 일반적으로 닫힌 형태(closed form)로 표현될 수 없어 수치적분을 사용해야 한다.
평균이 0이고 분산이 1인 정규분포를 표준정규분포(standard normal distribution)라고 하며, 확률변수를 \(Z\)로 표기한다.
\[Z \sim N(0, 1)\]
24.2 지수분포
지수분포(exponential distribution)는 사건이 일정한 비율로 발생하는 경우, 즉 사건 간 대기 시간이 무기억 속성(memoryless property)를 갖는 경우를 모형화한 것이다.
확률변수 \(X\)가 지수분포를 따른다면, 이를 \(X \sim Exp(\lambda)\)로 표기하고 확률밀도함수(PDF)는 다음과 같다.
\[f(x) = \lambda e^{-\lambda x} \qquad x \geq 0\]
\(\lambda\)는 사건 발생 비율을 나타내는 지수분포 모수다. 지수분포의 누적분포함수(CDF)는 다음과 같이 정의된다.
\[F(x) = P(X \leq x) = 1 - e^{-\lambda x} \text{ for } x \geq 0\]
평균 \(E(X) = \frac{1}{\lambda}\)이고 분산 \(Var(X) = \frac{1}{\lambda^2}\)이다.
지수분포의 확률밀도함수(PDF)로부터 누적분포함수(CDF)를 유도하는 과정은 다음과 같다. 먼저 지수분포의 PDF는 다음과 같이 정의된다.
\[f(x) = \lambda e^{-\lambda x} \qquad x \geq 0\]
CDF는 PDF를 확률변수 \(X\)의 가능한 모든 값의 범위에 대해 적분하여 얻는다.
\[F(x) = \int_{0}^{x} f(t) dt\]
이제 \(f(t) = \lambda e^{-\lambda t}\) 를 적분하면 다음과 같이 계산된다.
적분 설정 \[F(x) = \int_{0}^{x} \lambda e^{-\lambda t} dt\]
적분 수행 적분 과정을 통해 함수 \(\lambda e^{-\lambda t}\)를 \(t\) 에 대해 0부터 \(x\) 까지 적분한다.
\[F(x) = \left[ -e^{-\lambda t} \right]_{0}^{x} = -e^{-\lambda x} + e^{-\lambda \cdot 0}\] \[F(x) = -e^{-\lambda x} + 1\]
최종 결과 \[F(x) = 1 - e^{-\lambda x}\]
24.3 감마분포
감마분포(gamma distribution)는 지수분포를 일반화한 것으로, 알파(\(\alpha\))와 베타(\(\beta\))의 두 모수로 특징지어진다.
확률변수 \(X\)가 감마분포를 따른다면, \(X \sim Gamma(\alpha, \beta)\)로 표기하고 확률밀도함수(PDF)는 다음과 같다.
\[f(x) = \frac{\beta^\alpha}{\Gamma(\alpha)}x^{\alpha-1}e^{-\beta x} \text{ for } x > 0\]
여기서 \(\Gamma(\alpha)\)는 감마 함수로 다음과 같이 정의된다.
\[\Gamma(\alpha) = \int\_0^\infty t^{\alpha-1}e^{-t}dt\]
감마분포의 누적분포함수(CDF)는 다음과 같이 정의된다.
\[F(x) = P(X \leq x) = \frac{\gamma(\alpha, \beta x)}{\Gamma(\alpha)} \text{ for } x > 0\]
여기서 \(\gamma(\alpha, \beta x)\)는 하부 불완전 감마 함수(lower incomplete gamma function)로 다음과 같이 정의된다.
\[\gamma(\alpha, \beta x) = \int_0^{\beta x} t^{\alpha-1}e^{-t}dt\]
평균 \(E(X) = \frac{\alpha}{\beta}\)이고 분산 \(Var(X) = \frac{\alpha}{\beta^2}\)이다.
형상모수(shape parameter) \(\alpha\)가 자연수일 때의 감마분포를 얼랑분포(Erlang distribution)라고 한다.
자유도(degrees of freedom) \(n\)을 형상모수로 하고 척도모수(scale parameter) \(\beta = \frac{1}{2}\)인 감마분포를 카이제곱분포(chi-square distribution)라고 한다.
\[X \sim \chi^2(n) \text{ 만약 } X \sim \Gamma(\frac{n}{2}, \frac{1}{2})\]
24.4 베타분포
베타분포(beta distribution)는 알파(\(\alpha\))와 베타(\(\beta\))의 두 모수로 특징지어지는 연속형 확률분포로, 확률변수 \(X\)가 베타분포를 따른다면 이를 \(X \sim Beta(\alpha, \beta)\)로 표기하고 확률밀도함수(PDF)는 다음과 같다.
\[f(x) = \frac{x^{\alpha-1}(1-x)^{\beta-1}}{B(\alpha, \beta)} \qquad 0 < x < 1\]
\(B(\alpha, \beta)\)는 베타 함수로 다음과 같이 정의된다.
\[B(\alpha, \beta) = \int\_0^1 t^{\alpha-1}(1-t)^{\beta-1}dt = \frac{\Gamma(\alpha)\Gamma(\beta)}{\Gamma(\alpha + \beta)}\]
베타분포의 누적분포함수(CDF)는 다음과 같이 정의된다.
\[F(x) = P(X \leq x) = \frac{B(x; \alpha, \beta)}{B(\alpha, \beta)} \text{ for } 0 \leq x \leq 1\]
\(B(x; \alpha, \beta)\)는 불완전 베타 함수(incomplete beta function)로 다음과 같이 정의된다.
\[B(x; \alpha, \beta) = \int_0^x t^{\alpha-1}(1-t)^{\beta-1}dt\]
평균 \(E(X) = \frac{\alpha}{\alpha + \beta}\)이고 분산 \(Var(X) = \frac{\alpha\beta}{(\alpha+\beta)^2(\alpha+\beta+1)}\)이다.