13  검정

R.A. 피셔(Fisher)는 NHST의 토대를 만들었으며 분산분석의 개념과 제한된 표본을 이용해 실험을 설계하는 실험계획법에 큰 기여를 했다. 1925년에 그가 발표한 ’Statistical Methods for Research Workers’라는 책에서 유의성 검정(significance test) 개념이 소개된 것을 확인할 수 있다. (Fisher, 1970)

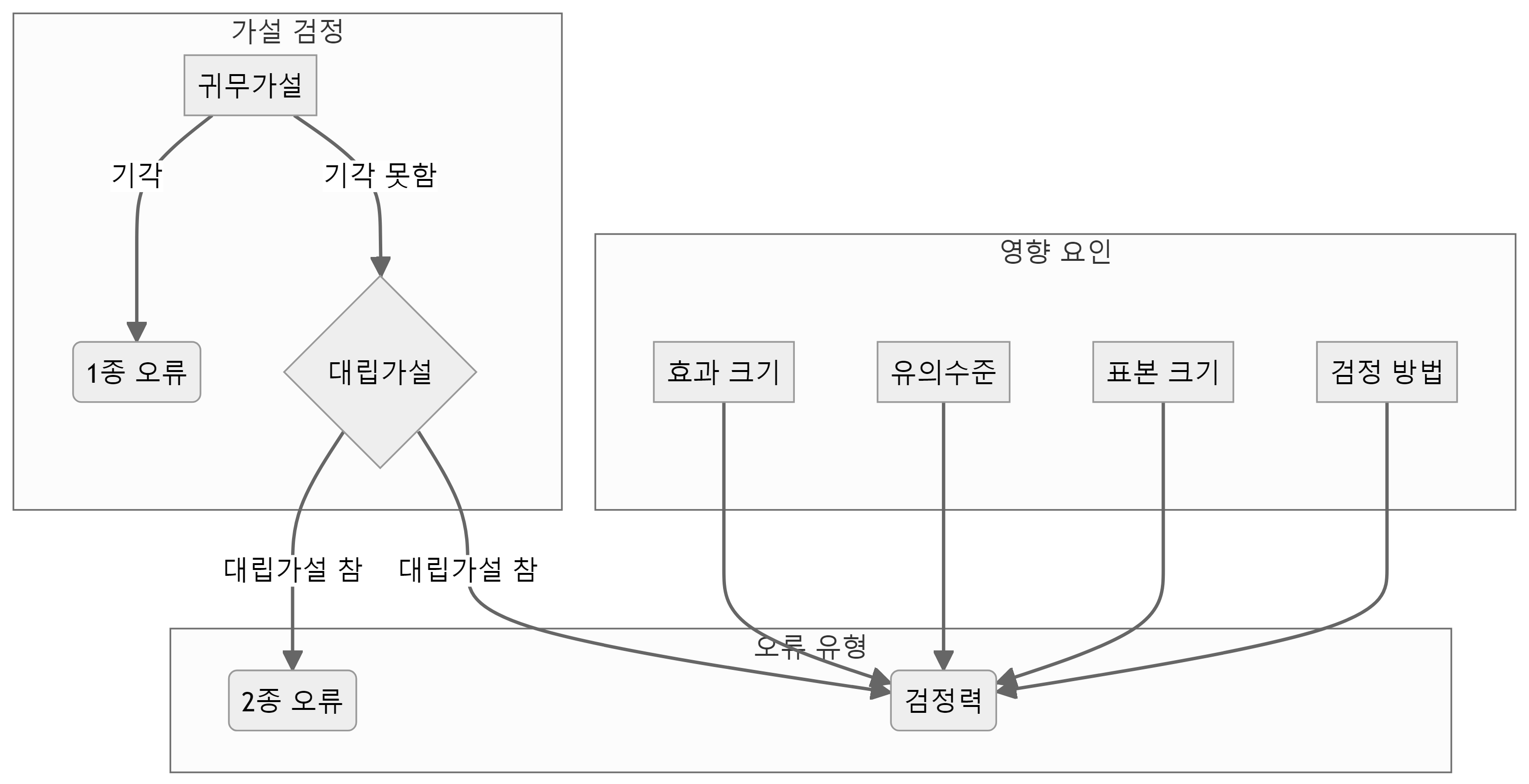
귀무가설(null hypothesis)과 대립가설(alternative hypothesis)을 바탕으로 한 가설검정(hypothesis testing) 개념을 네이만(Neyman)과 피어슨(Pearson)이 정립했고, 이를 적용한 최초의 사례는 1940년에 발표한 “Statistical Analysis in Educational Research”라는 책에서 NHST(Null Hypothesis Significance Testing) 개념을 처음으로 사용한 것으로 알려져 있다. (Lindquist, 1940)

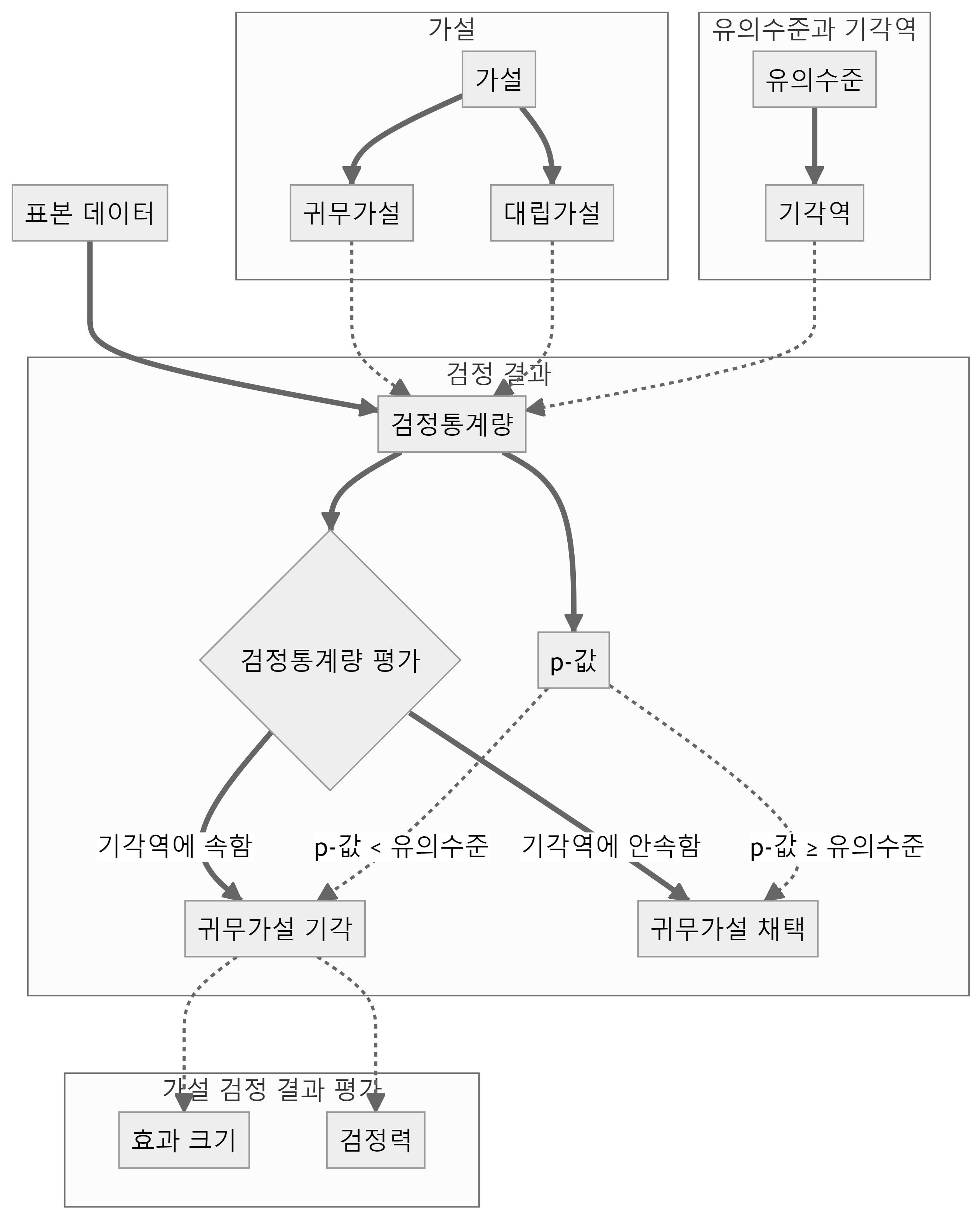
통계 검정에서 가설, 유의수준, 검정통계량, 기각역, p-값, 검정력, 효과크기를 중요 개념으로 다루고 있다.

1. 가설

• 귀무가설 (\(H_0\)): 연구자가 기각하고자 하는 가설로, 일반적으로 “효과가 없다” 또는 “차이가 없다”와 같은 형태로 나타낸다.
• 대립가설 (\(H_1\) 또는 \(H_a\)): 연구자가 증명하고자 하는 가설로, 귀무가설과 반대되는 내용을 포함한다.

2. 유의수준 (\(\alpha\))

• 귀무가설이 참임에도 불구하고 기각하는 오류(제1종 오류)를 범할 확률의 최대 허용 한계를 의미한다.
• 일반적으로 \(\alpha\)는 0.01, 0.05, 0.1 등의 값으로 설정한다.

3. 검정통계량

• 표본 데이터를 요약한 값으로, 가설을 검정하는 데 사용된다.
• 예를 들어, 두 모평균 차이에 대한 검정에서는 t-통계량을 사용한다. \(\bar{X}_1\), \(\bar{X}_2\)는 각 표본의 평균, \(s_p\)는 합동 표준편차, \(n_1\), \(n_2\)는 각 표본의 크기다.

\[t = \frac{\bar{X}_1 - \bar{X}_2}{s_p \sqrt{\frac{1}{n_1} + \frac{1}{n_2}}}\]

4. 기각역 (Critical Region)

• 귀무가설을 기각하기로 결정하는 검정통계량의 범위를 의미한다.
• 기각역은 유의수준 \(\alpha\)에 따라 결정되며, 양측 검정의 경우 기각역은 양쪽 꼬리 부분에 위치한다.
• 예를 들어, 유의수준 \(\alpha\)가 0.05인 양측 검정에서는 기각역이 \((-\infty, -z_{\alpha/2}) \cup (z_{\alpha/2}, \infty)\)로 정의된다. \(z_{\alpha/2}\)는 표준정규분포의 상위 \(\alpha/2\) 분위수이다.

5. p-값 (p-value)

• 관측된 검정통계량보다 극단적인 값이 나올 확률을 의미한다. 귀무가설이 참이라는 가정 하에 산출된다.
• p-값이 유의수준 \(\alpha\)보다 작으면 귀무가설을 기각하게 된다.
• p-값은 다음과 같이 계산할 수 있다. \(T\)는 검정통계량, \(t_{obs}\)는 관측된 검정통계량 값이다.

\[p-value = P(|T| \geq |t_{obs}| \mid H_0)\]

6. 검정력 (Power)

• 귀무가설이 거짓일 때 이를 기각할 확률을 의미한다.
• 검정력은 1종 오류(\(\alpha\))와 2종 오류(\(\beta\))의 확률, 효과 크기, 표본 크기에 따라 달라진다.
• 검정력은 다음과 같이 표현할 수 있다.

\[Power = P(\text{Reject } H_0 \mid H_1 \text{ is true}) = 1 - \beta\]

7. 효과 크기 (Effect Size)

• 연구 결과의 실질적 중요성을 나타내는 지표다.
• 효과 크기는 집단 간 차이나 변수 간 관계의 강도를 표현한다.
• 예를 들어, Cohen’s d는 두 집단 간 평균 차이를 공통 표준편차로 나눈 값으로 정의된다. \(\mu_1\), \(\mu_2\)는 각 집단의 모평균, \(\sigma\)는 공통 모표준편차다.

\[d = \frac{\mu_1 - \mu_2}{\sigma}\]

13.1 가설검정 개념

가설검정은 표본 데이터를 이용하여 모집단에 대한 주장이나 가설을 검증하는 통계적 방법이다. 가설검정에서는 연구자가 세운 가설을 귀무가설(null hypothesis, \(H_0\))과 대립가설(alternative hypothesis, \(H_1\))로 구분한다.

• 귀무가설(\(H_0\)): 연구자가 기각하고자 하는 가설, 보통 “차이가 없다” 또는 “효과가 없다”와 같은 형태로 설정
• 대립가설(\(H_1\)): 연구자가 증명하고자 하는 가설, 귀무가설과 반대되는 내용

가설검정은 귀무가설이 참이라는 전제 하에, 표본 데이터가 귀무가설과 얼마나 일치하는지를 평가한다. 만약 데이터가 귀무가설과 크게 다르다면, 귀무가설을 기각하고 대립가설을 채택한다.

13.2 가설검정 절차

1. 귀무가설과 대립가설을 설정한다.
2. 유의수준(\(\\alpha\))을 선택한다 (일반적으로 0.05 또는 0.01).
3. 데이터를 수집하고 분석한다.
4. 검정 통계량(예: t-통계량, z-통계량, F-통계량 등)을 계산한다.
5. 검정 통계량을 임계값(critical value)과 비교한다.
6. p-값(p-value)을 계산하고, 유의수준과 비교하여 귀무가설을 기각할지 결정한다.
   • p-값 \(\\leq\) 유의수준(\(\\alpha\)): 귀무가설을 기각하고 대립가설을 채택
   • p-값 > 유의수준(\(\\alpha\)): 귀무가설을 기각하지 않음
7. 결과를 해석하고 보고한다.

13.3 유의수준과 p-값

유의수준(\(\alpha\))은 제1종 오류(Type I error), 즉 귀무가설이 참임에도 불구하고 이를 기각할 확률의 최대 허용 한계를 의미한다. 사전에 설정하며 일반적으로 0.05 또는 0.01을 사용한다.

p-값은 귀무가설이 참이라는 가정 하에, 관측된 데이터 또는 그보다 극단적인 데이터가 나타날 확률을 의미한다. p-값이 작을수록 귀무가설을 기각할 증거가 강해진다.

13.4 가설검정의 종류

가설검정은 검정 대상에 따라 다양한 종류로 나뉜다. 몇 가지 주요 가설검정 방법은 다음과 같다.

1. t-검정(t-test): 한 집단 또는 두 집단의 평균 차이를 검정
2. 분산분석(ANOVA): 세 집단 이상의 평균 차이를 검정
3. 카이제곱 검정(\(\chi^2\) test): 범주형 변수 간의 관계 또는 독립성을 검정

13.5 가설검정의 한계

가설검정은 유용한 통계적 도구이지만, 한계도 명확히 존재한다.

1. 표본 크기에 영향을 받음: 표본 크기가 큰 경우 작은 차이도 통계적으로 유의한 것으로 나타날 수 있음
2. 실질적 유의성(practical significance)을 고려하지 않음: 통계적 유의성이 실제 효과의 크기나 중요성을 반영하지 않을 수 있음
3. 연구자의 주관적 판단 개입: 유의수준 설정, 가설 설정 등에 연구자의 주관이 개입할 수 있음

따라서 가설검정 결과를 해석할 때는 이러한 한계점을 고려하고, 다른 통계 기법과 함께 종합적으로 판단해야 한다.

13.6 검정 분류

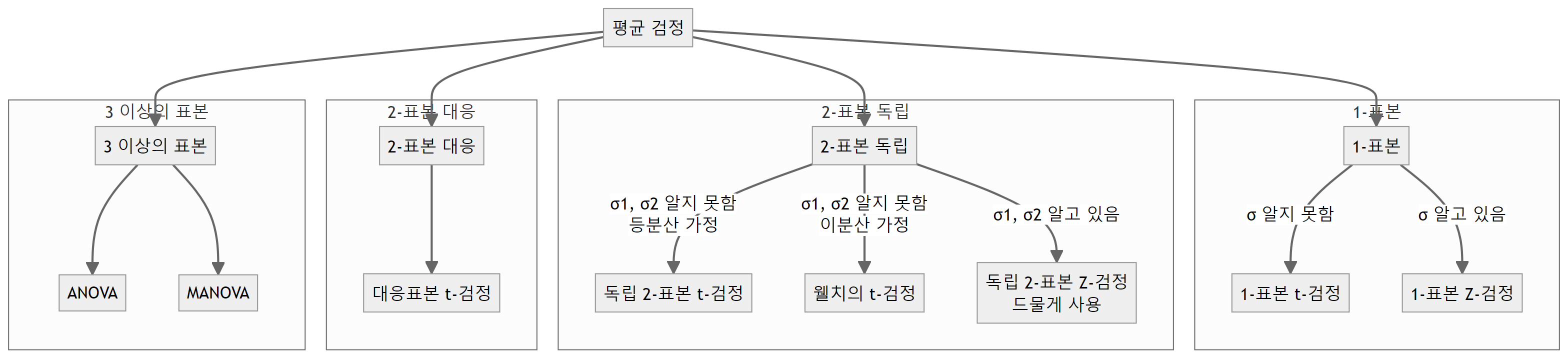
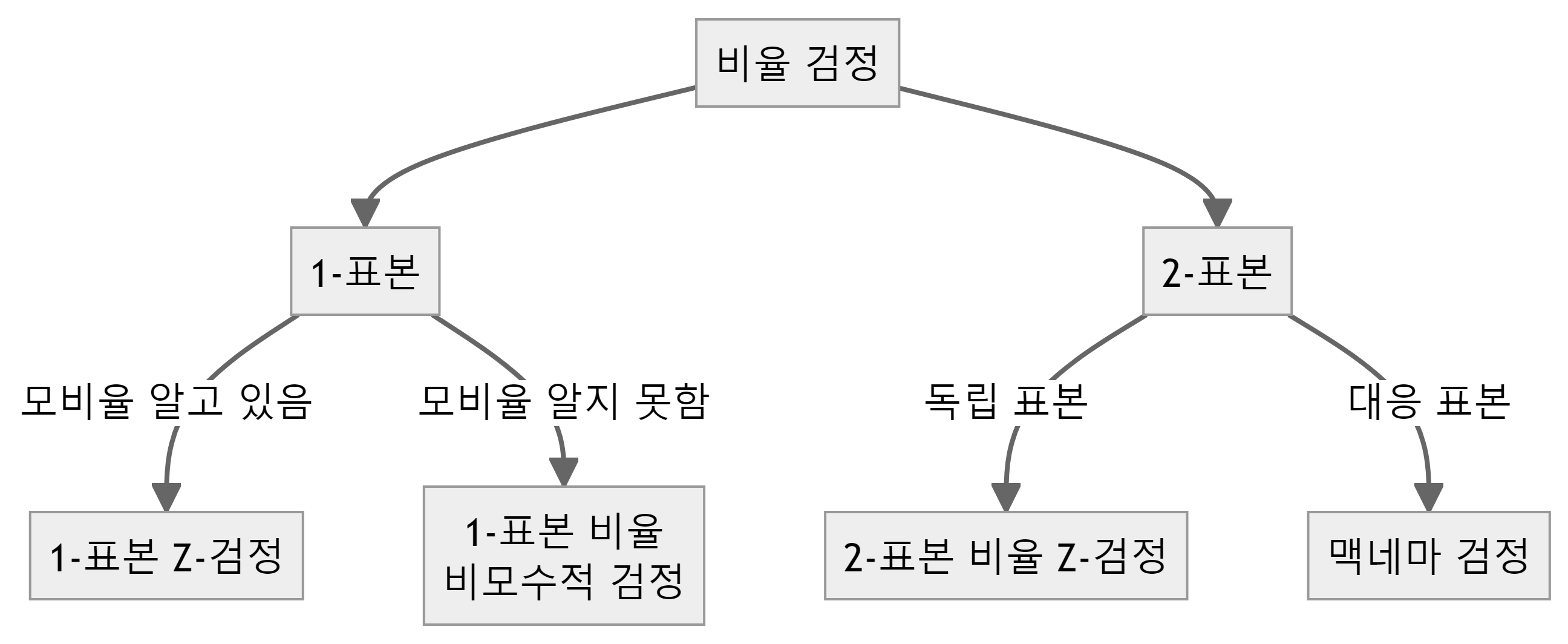
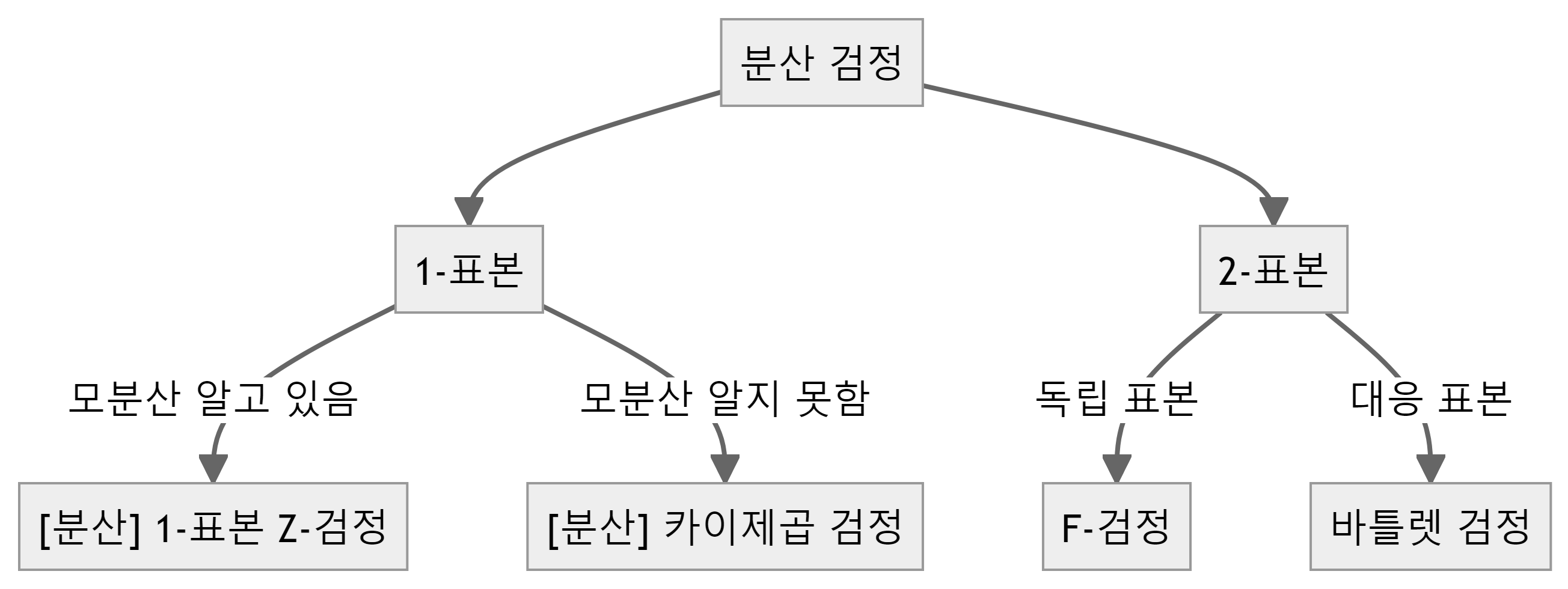
통계적 검정은 모수에 대한 검정, 변수 간 관계 검정, 가정 검정으로 분류된다. 모수에 대한 검정에는 평균 검정, 비율 검정, 분산 검정이 포함된다. 평균 검정은 1-표본과 2-표본 t-검정 및 Z-검정, ANOVA와 MANOVA로 나뉜다. 비율 검정은 1-표본과 2-표본 비율 검정으로 구성된다. 분산 검정은 1-표본과 2-표본 분산 검정으로 이루어진다.

변수 간 관계 검정에는 상관관계 검정, 독립성 검정, 적합도 검정이 있다. 상관관계 검정은 피어슨 상관계수와 스피어만 순위 상관계수로 나뉜다. 독립성 검정과 적합도 검정은 카이제곱 검정을 사용한다.

가정 검정에는 정규성 검정과 동질성 검정이 포함된다. 정규성 검정은 콜모고로프-스미르노프 검정과 샤피로-윌크 검정으로 이루어진다. 동질성 검정은 레빈 검정을 사용한다.

13.6.1 평균검정

13.6.2 비율검정

13.6.3 분산 검정

13.6.4 변수간 관계 검정

13.7 shiny 앱

#| label: fig-shiny-testing-helper
#| viewerHeight: 600
#| standalone: true

library(shiny)

ui <- fluidPage(
  tags$script(type = "text/x-mathjax-config",
              "MathJax.Hub.Config({
      tex2jax: {
        inlineMath: [['$', '$'], ['\\(', '\\)']],
        displayMath: [['$$', '$$'], ['\\[', '\\]']],
        processEscapes: true
      }
    });"
  ),
  tags$script(src = "https://cdnjs.cloudflare.com/ajax/libs/mathjax/2.7.7/MathJax.js?config=TeX-MML-AM_CHTML"),

  titlePanel("통계 검정 선택 도우미"),

  sidebarLayout(
    sidebarPanel(
      selectInput("test_category", "검정 분류",
                  choices = c("모수에 대한 검정", "변수 간 관계 검정", "가정 검정")),

      conditionalPanel(
        condition = "input.test_category == '모수에 대한 검정'",
        selectInput("parameter_test", "모수 검정 유형",
                    choices = c("평균 검정", "비율 검정", "분산 검정"))
      ),

      conditionalPanel(
        condition = "input.parameter_test == '평균 검정'",
        selectInput("mean_test", "평균 검정 유형",
                    choices = c("1-표본", "2-표본 독립", "2-표본 대응", "3 이상의 표본"))
      ),

      conditionalPanel(
        condition = "input.parameter_test == '비율 검정'",
        selectInput("proportion_test", "비율 검정 유형",
                    choices = c("1-표본", "2-표본"))
      ),

      conditionalPanel(
        condition = "input.parameter_test == '분산 검정'",
        selectInput("variance_test", "분산 검정 유형",
                    choices = c("1-표본", "2-표본"))
      ),

      conditionalPanel(
        condition = "input.test_category == '변수 간 관계 검정'",
        selectInput("relation_test", "변수 간 관계 검정 유형",
                    choices = c("상관관계 검정", "독립성 검정", "적합도 검정"))
      ),

      conditionalPanel(
        condition = "input.test_category == '가정 검정'",
        selectInput("assumption_test", "가정 검정 유형",
                    choices = c("정규성 검정", "동질성 검정"))
      )
    ),

    mainPanel(
      h4("선택된 통계 검정:"),
      textOutput("selected_test"),
      h4("검정 설명:"),
      uiOutput("test_description")
    )

  )
)

server <- function(input, output) {

  output$selected_test <- renderText({
    if (input$test_category == "모수에 대한 검정") {
      if (input$parameter_test == "평균 검정") {
        if (input$mean_test == "1-표본") {
          "1-표본 t-검정 또는 1-표본 Z-검정"
        } else if (input$mean_test == "2-표본 독립") {
          "독립 2-표본 t-검정, 웰치의 t-검정 또는 독립 2-표본 Z-검정"
        } else if (input$mean_test == "2-표본 대응") {
          "대응표본 t-검정"
        } else {
          "ANOVA 또는 MANOVA"
        }
      } else if (input$parameter_test == "비율 검정") {
        if (input$proportion_test == "1-표본") {
          "1-표본 Z-검정 또는 1-표본 비율 비모수적 검정"
        } else {
          "2-표본 비율 Z-검정 또는 맥네마 검정"
        }
      } else {
        if (input$variance_test == "1-표본") {
          "1-표본 Z-검정 또는 카이제곱 검정"
        } else {
          "F-검정 또는 바틀렛 검정"
        }
      }
    } else if (input$test_category == "변수 간 관계 검정") {
      if (input$relation_test == "상관관계 검정") {
        "피어슨 상관계수, 스피어만 순위 상관계수 또는 켄달 순위 상관계수"
      } else if (input$relation_test == "독립성 검정") {
        "카이제곱 독립성 검정, 피셔의 정확 검정 또는 맥네마 검정"
      } else {
        "카이제곱 적합도 검정, 콜모고로프-스미르노프 적합도 검정 또는 앤더슨-달링 검정"
      }
    } else {
      if (input$assumption_test == "정규성 검정") {
        "콜모고로프-스미르노프 검정 또는 샤피로-윌크 검정"
      } else {
        "레빈 검정"
      }
    }
  })

  output$test_description <- renderUI({
    if (input$test_category == "모수에 대한 검정") {
      if (input$parameter_test == "평균 검정") {
        if (input$mean_test == "1-표본") {
          withMathJax("1-표본 t-검정은 모집단의 평균이 특정 값과 같은지를 검정하는 데 사용됩니다. 검정통계량 t는 다음과 같이 계산됩니다:</p>
               $t = \\frac{\\bar{x} - \\mu_0}{s / \\sqrt{n}}$
               여기서 $\\bar{x}$는 표본평균, $\\mu_0$는 가설 평균값, $s$는 표본표준편차, $n$은 표본크기입니다.</p>
               예를 들어, 어떤 제품의 평균 중량이 100g인지 검정하고자 할 때 1-표본 t-검정을 사용할 수 있습니다.</p>")
        } else if (input$mean_test == "2-표본 독립") {
          withMathJax("독립 2-표본 t-검정은 두 모집단의 평균이 같은지를 검정하는 데 사용됩니다. 검정통계량 t는 다음과 같이 계산됩니다:</p>
               $t = \\frac{\\bar{x}_1 - \\bar{x}_2}{\\sqrt{s_p^2 (\\frac{1}{n_1} + \\frac{1}{n_2})}}$
               여기서 $\\bar{x}_1$와 $\\bar{x}_2$는 각 표본의 평균, $s_p^2$는 합동분산, $n_1$과 $n_2$는 각 표본의 크기입니다.</p>
               예를 들어, 두 다른 교육 방법이 학생들의 성적에 미치는 영향을 비교할 때 독립 2-표본 t-검정을 사용할 수 있습니다.</p>")
        } else if (input$mean_test == "2-표본 대응") {
          withMathJax("대응표본 t-검정은 동일한 개체에 대한 두 측정값 간 차이의 평균이 0인지를 검정하는 데 사용됩니다. 검정통계량 t는 다음과 같이 계산됩니다:</p>
               $t = \\frac{\\bar{d}}{s_d / \\sqrt{n}}$
               여기서 $\\bar{d}$는 차이의 평균, $s_d$는 차이의 표준편차, $n$은 표본크기입니다.</p>
               예를 들어, 신약 복용 전후의 혈압 변화를 검정할 때 대응표본 t-검정을 사용할 수 있습니다.</p>")
        } else {
          withMathJax("ANOVA(분산분석)는 세 집단 이상의 평균이 같은지를 검정하는 데 사용됩니다. 검정통계량 F는 다음과 같이 계산됩니다:</p>
               $F = \\frac{\\text{집단 간 변동} / \\text{자유도}_\\text{집단 간}}{\\text{집단 내 변동} / \\text{자유도}_\\text{집단 내}}$
               여기서 집단 간 변동은 집단 평균들의 차이로 인한 변동, 집단 내 변동은 집단 내 개체들의 차이로 인한 변동입니다.</p>
               예를 들어, 세 가지 학습 방법이 학업 성취도에 미치는 영향을 비교할 때 ANOVA를 사용할 수 있습니다.</p>")
        }
      } else if (input$parameter_test == "비율 검정") {
        if (input$proportion_test == "1-표본") {
          withMathJax("1-표본 비율 검정은 모집단의 비율이 특정 값과 같은지를 검정하는 데 사용됩니다. 검정통계량 Z는 다음과 같이 계산됩니다:</p>
               $Z = \\frac{\\hat{p} - p_0}{\\sqrt{p_0(1-p_0)/n}}$
               여기서 $\\hat{p}$는 표본비율, $p_0$는 가설 비율값, $n$은 표본크기입니다.</p>
               예를 들어, 어떤 제품의 불량률이 5%인지 검정하고자 할 때 1-표본 비율 검정을 사용할 수 있습니다.</p>")
        } else {
          withMathJax("2-표본 비율 검정은 두 모집단의 비율이 같은지를 검정하는 데 사용됩니다. 검정통계량 Z는 다음과 같이 계산됩니다:</p>
               $Z = \\frac{\\hat{p}_1 - \\hat{p}_2}{\\sqrt{\\hat{p}(1-\\hat{p})(\\frac{1}{n_1}+\\frac{1}{n_2})}}$
               여기서 $\\hat{p}_1$와 $\\hat{p}_2$는 각 표본의 비율, $\\hat{p}$는 합동비율, $n_1$과 $n_2$는 각 표본의 크기입니다.</p>
               예를 들어, 두 지역 간 흡연율의 차이를 검정할 때 2-표본 비율 검정을 사용할 수 있습니다.</p>")
        }
      } else {
        if (input$variance_test == "1-표본") {
          withMathJax("1-표본 분산 검정은 모집단의 분산이 특정 값과 같은지를 검정하는 데 사용됩니다. 검정통계량 $\\chi^2$는 다음과 같이 계산됩니다:</p>
               $\\chi^2 = \\frac{(n-1)s^2}{\\sigma_0^2}$
               여기서 $s^2$는 표본분산, $\\sigma_0^2$는 가설 분산값, $n$은 표본크기입니다.</p>
               예를 들어, 어떤 공정의 품질 변동이 규격 내에 있는지 검정하고자 할 때 1-표본 분산 검정을 사용할 수 있습니다.</p>")
        } else {
          withMathJax("2-표본 분산 검정(F-검정)은 두 모집단의 분산이 같은지를 검정하는 데 사용됩니다. 검정통계량 F는 다음과 같이 계산됩니다:</p>
               $F = \\frac{s_1^2}{s_2^2}$
               여기서 $s_1^2$와 $s_2^2$는 각 표본의 분산입니다.</p>
               예를 들어, 두 공정의 품질 변동성을 비교할 때 F-검정을 사용할 수 있습니다.</p>")
        }
      }
    } else if (input$test_category == "변수 간 관계 검정") {
      if (input$relation_test == "상관관계 검정") {
        withMathJax("상관관계 검정은 두 연속형 변수 간의 선형 관계를 검정하는 데 사용됩니다. 피어슨 상관계수 r은 다음과 같이 계산됩니다:</p>
             $r = \\frac{\\sum_{i=1}^{n} (x_i - \\bar{x})(y_i - \\bar{y})}{\\sqrt{\\sum_{i=1}^{n} (x_i - \\bar{x})^2} \\sqrt{\\sum_{i=1}^{n} (y_i - \\bar{y})^2}}$
             여기서 $x_i$와 $y_i$는 i번째 관측값, $\\bar{x}$와 $\\bar{y}$는 각 변수의 표본평균입니다.</p>
             예를 들어, 학생들의 공부 시간과 성적 간의 상관관계를 검정할 때 피어슨 상관계수를 사용할 수 있습니다.</p>")
      } else if (input$relation_test == "독립성 검정") {
        withMathJax("독립성 검정은 두 범주형 변수 간의 관련성을 검정하는 데 사용됩니다. 카이제곱 독립성 검정의 검정통계량 $\\chi^2$는 다음과 같이 계산됩니다:</p>
             $\\chi^2 = \\sum_{i=1}^{r} \\sum_{j=1}^{c} \\frac{(O_{ij} - E_{ij})^2}{E_{ij}}$
             여기서 $O_{ij}$는 i행 j열의 관측도수, $E_{ij}$는 i행 j열의 기대도수, $r$과 $c$는 각각 행과 열의 수입니다.</p>
             예를 들어, 성별과 흡연 여부 간의 관련성을 검정할 때 카이제곱 독립성 검정을 사용할 수 있습니다.</p>")
      } else {
        withMathJax("적합도 검정은 관측된 범주형 데이터의 분포가 이론적 분포와 일치하는지를 검정하는 데 사용됩니다. 카이제곱 적합도 검정의 검정통계량 $\\chi^2$는 다음과 같이 계산됩니다:</p>
             $\\chi^2 = \\sum_{i=1}^{k} \\frac{(O_i - E_i)^2}{E_i}$
             여기서 $O_i$는 i번째 범주의 관측도수, $E_i$는 i번째 범주의 기대도수, $k$는 범주의 수입니다.</p>
             예를 들어, 주사위의 각 면이 나올 확률이 균등한지 검정할 때 카이제곱 적합도 검정을 사용할 수 있습니다.</p>")
      }
    } else {
      if (input$assumption_test == "정규성 검정") {
        withMathJax("정규성 검정은 데이터가 정규분포를 따르는지를 검정하는 데 사용됩니다. 콜모고로프-스미르노프 검정의 검정통계량 D는 다음과 같이 계산됩니다:</p>
             $D = \\max_{1 \\leq i \\leq n} (F(x_i) - \\frac{i-1}{n}, \\frac{i}{n} - F(x_i))$
             여기서 $F(x)$는 가설 누적분포함수, $x_i$는 i번째 순서통계량입니다.</p>
             예를 들어, 회귀분석 전에 잔차의 정규성을 검정할 때 콜모고로프-스미르노프 검정을 사용할 수 있습니다.</p>")
      } else {
        withMathJax("동질성 검정은 두 개 이상의 집단 간 분산의 동질성을 검정하는 데 사용됩니다. 레빈 검정의 검정통계량 W는 다음과 같이 계산됩니다:</p>
             $W = \\frac{(N-k)}{(k-1)} \\frac{\\sum_{i=1}^{k} n_i (\\bar{Z}_{i\\cdot} - \\bar{Z}_{\\cdot\\cdot})^2}{\\sum_{i=1}^{k} \\sum_{j=1}^{n_i} (Z_{ij} - \\bar{Z}_{i\\cdot})^2}$
             여기서 $Z_{ij} = |X_{ij} - \\tilde{X}_i|$, $\\tilde{X}_i$는 i번째 집단의 중앙값, $\\bar{Z}_{i\\cdot}$는 i번째 집단의 $Z_{ij}$ 평균, $\\bar{Z}_{\\cdot\\cdot}$는 전체 $Z_{ij}$ 평균입니다.</p>
             예를 들어, 일원분산분석 전에 집단 간 분산의 동질성을 검정할 때 레빈 검정을 사용할 수 있습니다.</p>")
      }
    }
  })
}

shinyApp(ui, server)

13.8 효과크기

효과크기(effect size)는 두 집단 간의 차이의 크기, 변수들 간의 관계 강도, 통계적 검정 결과의 실질적 중요성을 평가하는 중요한 지표다. 효과크기를 해석하면 통계적 유의성과 연구 결과의 실무적 의의를 파악할 수 있다. 다양한 효과크기 지표가 있지만, 코헨 D(Cohen’s d), 피어슨 R(Pearson’s r), 오즈비(Odds Ratio)가 대표적이다.

코헨 D는 두 집단 간의 평균 차이를 표준 편차로 나눈 값으로 두 집단 간의 차이가 얼마나 큰지를 표준화된 방식으로 나타낸다. 즉, 두 집단 간의 평균 차이가 공통 표준편차 몇 배에 해당하는지를 나타내는 지표다. \(\bar{x}_1\)과 \(\bar{x}_2\)는 각 집단의 평균이고, \(s\)는 공통 표준편차다.

\[d = \frac{\bar{x}_1 - \bar{x}_2}{s}\]

#> [1] -0.9310935

피어슨 R(상관계수)은 두 변수 간의 선형 관계의 강도를 측정하는 지표로, -1에서 1 사이의 값을 갖는다. 0에 가까울수록 관계가 약하고, -1이나 1에 가까울수록 관계가 강하다.

\[ r = \frac{\sum_{i=1}^{n} (x_i - \bar{x})(y_i - \bar{y})}{\sqrt{\sum_{i=1}^{n} (x_i - \bar{x})^2} \sqrt{\sum_{i=1}^{n} (y_i - \bar{y})^2}} \]

#> [1] 0.4654914

오즈비는 두 범주형 변수 간의 관계의 강도를 측정하는 지표로, 한 범주에 속할 오즈(odds)를 다른 범주에 속할 오즈로 나눈 값이다. 두 사건의 발생 확률의 비율을 비교한다. 오즈비가 1보다 클 경우, 어떤 사건이 발생할 확률이 더 높음을 의미하며, 1보다 작으면 더 낮음을 의미합니다. \(p_1\)과 \(p_2\)는 각 범주에 속할 확률이다.

\[OR = \frac{p_1 / (1 - p_1)}{p_2 / (1 - p_2)}\]

#> [1] 6

13.9 Shiny 앱 (효과크기)

#| label: fig-shiny-effect-size
#| viewerHeight: 800
#| standalone: true

library(shiny)

ui <- fluidPage(
  titlePanel("효과크기 계산기"),

  sidebarLayout(
    sidebarPanel(
      selectInput("effect_size_type", "효과크기 유형",
                  choices = c("Cohen's d", "Pearson's r", "Odds Ratio")),

      conditionalPanel(
        condition = "input.effect_size_type == 'Cohen\\'s d'",
        numericInput("mean1", "집단 1 평균", value = 10),
        numericInput("mean2", "집단 2 평균", value = 12),
        numericInput("sd1", "집단 1 표준편차", value = 2),
        numericInput("sd2", "집단 2 표준편차", value = 2)
      ),

      conditionalPanel(
        condition = "input.effect_size_type == 'Pearson\\'s r'",
        textInput("x_values", "X 값 (쉼표로 구분)", value = "1,2,3,4,5"),
        textInput("y_values", "Y 값 (쉼표로 구분)", value = "2,4,6,8,10")
      ),

      conditionalPanel(
        condition = "input.effect_size_type == 'Odds Ratio'",
        numericInput("a", "집단 1 사건 발생 수", value = 30),
        numericInput("b", "집단 1 사건 미발생 수", value = 20),
        numericInput("c", "집단 2 사건 발생 수", value = 10),
        numericInput("d", "집단 2 사건 미발생 수", value = 40)
      ),

      actionButton("calculate", "계산")
    ),

    mainPanel(
      verbatimTextOutput("result"),
      htmlOutput("interpretation")
    )
  )
)

server <- function(input, output) {

  effect_size <- eventReactive(input$calculate, {
    if (input$effect_size_type == "Cohen's d") {
      d <- (input$mean1 - input$mean2) / sqrt((input$sd1^2 + input$sd2^2) / 2)
      list(type = "Cohen's d", value = d)
    } else if (input$effect_size_type == "Pearson's r") {
      x <- as.numeric(unlist(strsplit(input$x_values, ",")))
      y <- as.numeric(unlist(strsplit(input$y_values, ",")))
      r <- cor(x, y)
      list(type = "Pearson's r", value = r)
    } else if (input$effect_size_type == "Odds Ratio") {
      odds_ratio <- (input$a / input$b) / (input$c / input$d)
      list(type = "Odds Ratio", value = odds_ratio)
    }
  })

  output$result <- renderPrint({
    cat("효과크기 유형:", effect_size()$type, "\n")
    cat("효과크기 값:", round(effect_size()$value, 3), "\n")
  })

  output$interpretation <- renderUI({
    if (input$effect_size_type == "Cohen's d") {
      if (abs(effect_size()$value) < 0.2) {
        HTML("<p>Cohen's d 값이 0.2보다 작으므로, 효과크기가 작습니다.</p>")
      } else if (abs(effect_size()$value) < 0.5) {
        HTML("<p>Cohen's d 값이 0.2와 0.5 사이이므로, 효과크기가 중간 정도입니다.</p>")
      } else {
        HTML("<p>Cohen's d 값이 0.5보다 크므로, 효과크기가 큽니다.</p>")
      }
    } else if (input$effect_size_type == "Pearson's r") {
      if (abs(effect_size()$value) < 0.1) {
        HTML("<p>상관계수의 절대값이 0.1보다 작으므로, 효과크기가 작습니다.</p>")
      } else if (abs(effect_size()$value) < 0.3) {
        HTML("<p>상관계수의 절대값이 0.1과 0.3 사이이므로, 효과크기가 중간 정도입니다.</p>")
      } else {
        HTML("<p>상관계수의 절대값이 0.3보다 크므로, 효과크기가 큽니다.</p>")
      }
    } else if (input$effect_size_type == "Odds Ratio") {
      if (effect_size()$value < 1) {
        HTML("<p>오즈비가 1보다 작으므로, 부적 관계를 나타냅니다.</p>")
      } else if (effect_size()$value == 1) {
        HTML("<p>오즈비가 1이므로, 관계가 없습니다.</p>")
      } else {
        HTML("<p>오즈비가 1보다 크므로, 정적 관계를 나타냅니다.</p>")
      }
    }
  })
}

shinyApp(ui, server)

13.10 검정력

검정력(statistical power)은 귀무가설이 거짓일 때 이를 기각할 확률을 의미한다. 즉, 실제로 효과가 있는데 이를 올바르게 탐지해 내는 능력이다. 검정력은 1종 오류(\(\alpha\)), 2종 오류(\(\beta\)), 효과 크기, 표본 크기에 따라 달라진다.

• 1종 오류(\(\alpha\)): 귀무가설이 참임에도 불구하고 이를 기각할 확률
• 2종 오류(\(\beta\)): 귀무가설이 거짓임에도 불구하고 이를 기각하지 않을 확률

검정력은 1에서 2종 오류 확률(\(\beta\))을 뺀 값으로 정의된다.

\[\text{검정력} = 1 - \beta = P(\text{기각 } H_0 \mid H_1 \text{이 참})\]

검정력을 높이기 위해서는 다음과 같은 방법이 있다.

1. 효과 크기를 크게 한다.
2. 유의수준(\(\alpha\))를 높인다.
3. 표본 크기(\(n\))를 늘린다.
4. 더 효율적인 통계적 검정 방법을 사용한다.

일반적으로 검정력은 0.8 이상이 되어야 한다고 여겨진다. 이는 실제로 효과가 있을 때, 그 효과를 탐지해 낼 확률이 80% 이상이어야 한다는 것을 의미한다.

13.11 shiny 앱 (검정력)

#| label: fig-shiny-spline
#| viewerHeight: 800
#| standalone: true

library(shiny)
library(pwr)

ui <- fluidPage(
  titlePanel("검정력 계산"),
  sidebarLayout(
    sidebarPanel(
      sliderInput("effect_size", "효과 크기 (Cohen's d)",
                  min = 0.01, max = 1.0, value = 0.5, step = 0.01),
      sliderInput("sig_level", "유의수준 (α)",
                  min = 0.01, max = 0.1, value = 0.05, step = 0.01),
      sliderInput("sample_size", "표본 크기",
                  min = 10, max = 200, value = 100, step = 5),
      actionButton("calculate", "검정력 계산")
    ),
    mainPanel(
      verbatimTextOutput("power_result"),
      plotOutput("power_plot"),
      htmlOutput("power_description")
    )
  )
)

server <- function(input, output) {
  # Reactive event for power calculation
  power_result <- eventReactive(input$calculate, {
    pwr.t.test(d = input$effect_size,
               sig.level = input$sig_level,
               n = input$sample_size,
               type = "two.sample",
               alternative = "two.sided")$power
  })

  # Display the calculated power
  output$power_result <- renderPrint({
    cat("검정력: ", round(power_result(), 3))
  })

  # Generate and render a plot of power vs. effect size
  output$power_plot <- renderPlot({
    plot(pwr.t.test(d = seq(0.2, 0.8, 0.1),
                    sig.level = input$sig_level,
                    n = input$sample_size,
                    type = "two.sample",
                    alternative = "two.sided",
                    power = NULL)$power ~ seq(0.2, 0.8, 0.1),
         type = "l",
         xlab = "Effect Size (Cohen's d)",
         ylab = "Power",
         main = "Power vs. Effect Size")
  })

  # Detailed description of how power is calculated
  output$power_description <- renderUI({
    HTML(paste0(
      "<h3>검정력 계산 과정:</h3>",
      "<p>1. 효과 크기 (Cohen's d)를 입력합니다. 이는 두 집단 간의 표준화된 평균 차이를 나타냅니다.</p>",
      "<p>2. 유의수준 (α)을 입력합니다. 이는 귀무가설이 참임에도 불구하고 이를 기각할 확률을 의미합니다.</p>",
      "<p>3. 표본 크기를 입력합니다. 이는 각 집단에서 수집된 데이터의 개수를 나타냅니다.</p>",
      "<p>4. 'pwr' 패키지의 'pwr.t.test' 함수를 사용하여 검정력을 계산합니다. 이 함수는 입력된 효과 크기, 유의수준, 표본 크기를 바탕으로 독립표본 t-검정에 대한 검정력을 계산합니다.</p>",
      "<p>5. 계산된 검정력이 출력됩니다.</p>",
      "<h3>검정력 그래프 설명:</h3>",
      "<p>그래프는 입력된 유의수준과 표본 크기를 고정한 상태에서, 효과 크기 (Cohen's d)에 따른 검정력의 변화를 보여줍니다. 효과 크기가 클수록 검정력이 높아지는 것을 확인할 수 있습니다. 이는 효과 크기가 클수록 귀무가설이 거짓일 때 이를 정확하게 기각할 확률이 높아짐을 의미합니다.</p>"
    ))
  })
}

shinyApp(ui, server)

13.12 검정 방법 선택

검정 방법의 선택은 연구 질문, 데이터 유형, 가정 등에 따라 달라지며, 적절한 검정 방법을 선택하는 것은 통계적 추론의 타당성을 확보하는 데 매우 중요한 역할을 한다.

1. 연구 질문과 가설에 부합하는 검정 방법 선택: 연구자는 연구 질문과 가설에 적합한 검정 방법을 선택해야 한다. 예를 들어, 두 집단 간 평균 차이를 검정하고자 할 때는 t-검정이나 ANOVA를 사용할 수 있다. 반면, 변수 간 관계를 검정하고자 할 때는 상관분석이나 회귀분석을 사용할 수 있다.

2. 데이터 유형을 고려한 검정 방법 선택: 데이터의 유형(연속형, 범주형, 순위형 등)에 따라 적절한 검정 방법을 선택해야 한다. 연속형 데이터에는 t-검정, ANOVA, 상관분석 등을 사용할 수 있으며, 범주형 데이터에는 카이제곱 검정, 피셔의 정확 검정 등을 사용할 수 있다.

3. 검정 가정 충족 여부 확인: 각 검정 방법은 특정 가정(정규성, 등분산성, 독립성 등)을 전제로 하기 때문에 가정이 충족되지 않으면 검정 결과의 타당성이 위협받을 수 있다. 따라서 연구자는 검정 가정의 충족 여부를 확인하고, 필요한 경우 비모수 검정 방법을 사용해야 한다.

4. 연구 설계에 적합한 검정 방법 선택: 연구 설계(실험 설계, 준실험 설계, 조사 설계 등)에 따라 적절한 검정 방법을 선택해야 한다. 예를 들어, 독립표본 설계에는 독립표본 t-검정을 사용하고, 대응표본 설계에는 대응표본 t-검정을 사용한다.

5. 다중 검정 문제 고려: 여러 개의 가설을 동시에 검정할 때는 다중 검정 문제를 고려해야 한다. 다중 검정으로 인해 1종 오류가 증가할 수 있으므로, Bonferroni 교정, Holm 교정, FDR(False Discovery Rate) 등의 방법을 사용하여 이를 통제해야 한다.

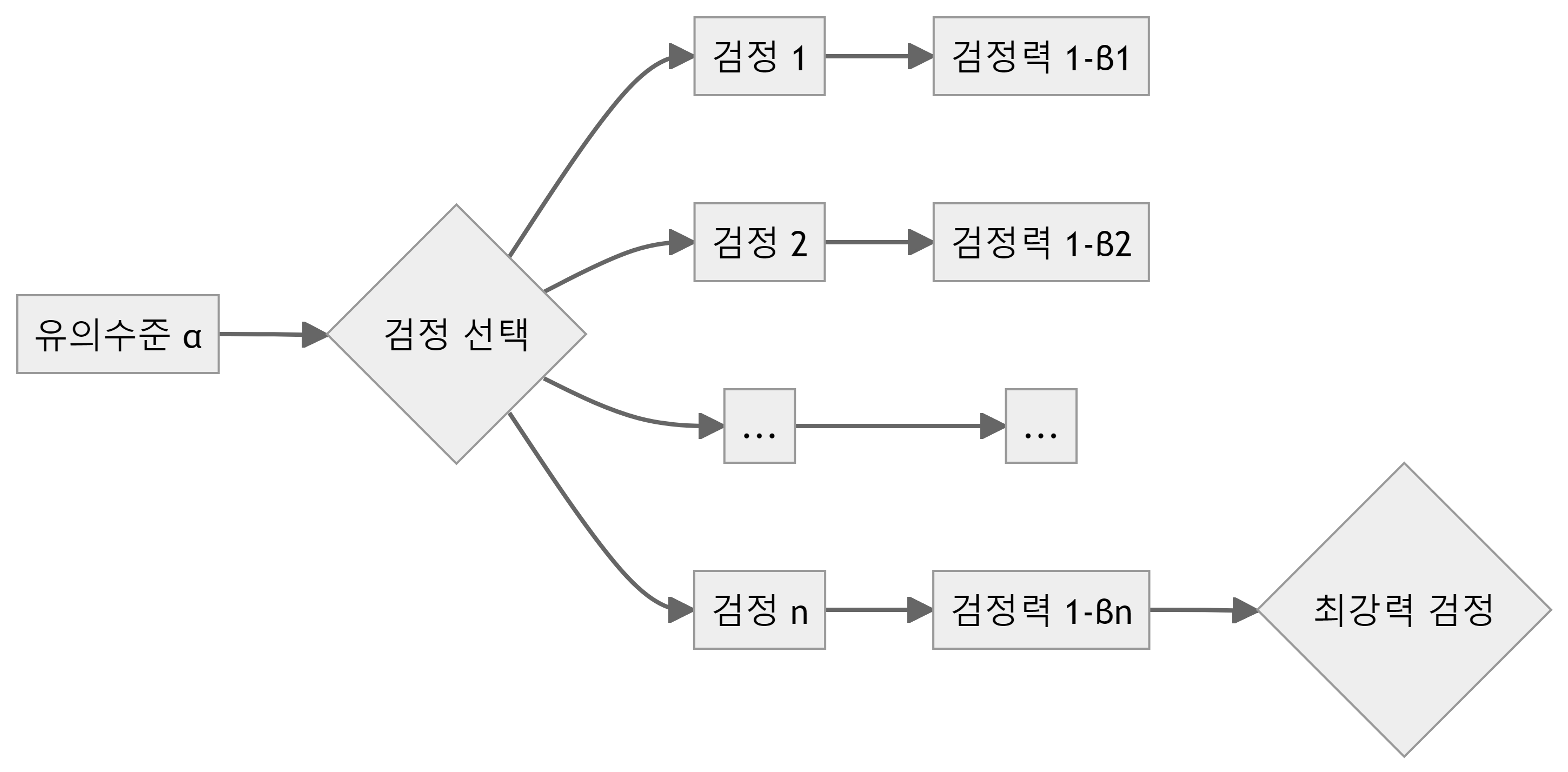
13.13 최강력 검정

최강력 검정(most powerful test)은 주어진 유의수준(1종 오류의 확률)에서 대립가설이 참일 때 귀무가설을 기각할 확률(검정력)이 가장 높은 검정을 의미한다. 즉, 최강력 검정은 주어진 조건에서 가장 높은 통계적 검출력을 가진 검정이다.

최강력 검정의 이론적 기반은 네이만-피어슨 보조정리(Neyman-Pearson Lemma)에 의해 뒷받침된다. 단순 대립가설에 대하여 유의수준이 \(\alpha\)인 검정 중에서 검정력이 가장 높은 검정(최강력 검정)은 우도비 검정(likelihood ratio test)이라는 것을 보여준다.

우도비 검정통계량은 다음과 같이 정의된다.

\[\Lambda = \frac{L(\theta_0)}{L(\hat{\theta})}\]

\(L(\theta_0)\)는 귀무가설 \(H_0: \theta = \theta_0\) 하에서의 우도 함수이고, \(L(\hat{\theta})\)는 모수 공간에서의 최대 우도 함수이다. 우도비 검정은 \(\Lambda\)이 작을수록(또는 \(-2\log\Lambda\)가 클수록) 귀무가설을 기각한다.

하지만 실제 연구에서는 대부분의 대립가설이 복합 가설(composite hypothesis)이므로, 최강력 검정을 직접 구현하는 것이 어려울 수 있다. 이 경우 국소 최강력 검정(locally most powerful test), 균일 최강력 검정(uniformly most powerful test) 등의 개념을 사용하여 최강력 검정에 근사하는 검정을 찾는다.

예를 들어, 정규분포 \(N(\mu, \sigma^2)\)에서 \(\mu\)에 대한 검정을 수행할 때, \(\sigma^2\)이 알려져 있다면 \(Z = \frac{\bar{X} - \mu_0}{\sigma/\sqrt{n}}\)이 최강력 검정통계량이 된다. 하지만 \(\sigma^2\)이 알려져 있지 않다면, \(T = \frac{\bar{X} - \mu_0}{S/\sqrt{n}}\)이 국소 최강력 검정통계량이 된다.

13.14 검정력과 최강력검정

검정력과 최강력 검정은 밀접한 관련이 있다. 검정력은 귀무가설이 거짓일 때 이를 정확히 기각할 확률을 의미하는 반면, 최강력 검정은 주어진 유의수준에서 검정력을 최대화하는 검정이다.

주어진 유의수준 \(\alpha\)에서 여러 검정 중 하나를 선택한다. 각 검정은 고유한 검정력을 가지고 있으며 최강력 검정은 이 중 검정력이 가장 높은 검정이다.

귀무가설 \(H_0: \theta \in \Theta_0\)와 대립가설 \(H_1: \theta \in \Theta_1\)이 있다고 가정하면 유의수준 \(\alpha\)에서 검정 \(\phi\)의 검정력은 다음과 같이 정의된다. \(\phi(X)\)는 귀무가설을 기각하면 1, 기각하지 않으면 0의 값을 가지는 검정 함수다.

\[\beta(\theta) = E_{\theta}(\phi(X)) = P_{\theta}(H_0 \text{ 기각} ), \quad \theta \in \Theta_1\]

최강력 검정 \(\phi^*\)는 모든 \(\theta \in \Theta_1\)에 대해 다음을 만족한다. \(\beta_{\phi^*}(\theta)\)와 \(\beta_{\phi}(\theta)\)는 각각 최강력 검정과 임의의 다른 검정의 검정력이다.

\[\beta_{\phi^*}(\theta) \geq \beta_{\phi}(\theta)\]

즉, 최강력 검정은 대립가설이 사실일 때, 주어진 유의수준에서 귀무가설을 기각할 확률이 가장 높은 검정으로 네이만-피어슨 보조정리에 의해 보장되며, 우도비 검정이 최강력 검정의 형태를 가지는 경우가 많다.

그러나 최강력 검정은 특정 대립가설에 의존하므로, 모든 상황에서 최강력 검정을 찾는 것은 쉽지 않다. 이에 따라 국소 최강력 검정, 균일 최강력 검정 등의 개념이 도입되었다.

13.14.1 제품 불량률 검정 사례

한 제조업체에서 생산한 제품의 불량률이 기준치 이하인지를 검정하고자 한다. 기준치는 5%이며, 기준치보다 불량률이 높은 경우 제조 공정에 문제가 있는 것으로 판단한다. 대립가설은 불량률이 5%보다 높다는 것이다.

• \(H_0: p \leq 0.05\) (불량률이 5% 이하)
• \(H_1: p > 0.05\) (불량률이 5% 초과)

제조업체는 100개의 제품을 무작위로 선택하여 불량 여부를 검사하였고, 그 중 10개가 불량품으로 판정되었다.

이 경우 이항분포를 사용하여 정확 검정(exact test)을 수행할 수 있다. 정확 검정은 이항분포에서 표본 크기가 작을 때 사용되며, 근사적인 방법(예: z-검정)에 비해 정확한 결과를 제공한다.

#> 
#>  Exact binomial test
#> 
#> data:  x and n
#> number of successes = 10, number of trials = 100, p-value = 0.02819
#> alternative hypothesis: true probability of success is greater than 0.05
#> 95 percent confidence interval:
#>  0.05526324 1.00000000
#> sample estimates:
#> probability of success 
#>                    0.1

이항분포 정확 검정 결과, p-값은 0.0281883로 유의수준 0.05보다 작다. 따라서 귀무가설을 기각하고 대립가설을 채택할 수 있다. 즉, 이 결과는 제품의 불량률이 5%보다 유의하게 높다는 것을 시사한다.

사실 이 경우 귀무가설이 복합 가설(\(p \leq 0.05\))이므로 최강력 검정을 직접 구할 수는 없다. 그러나 이항분포의 정확 검정은 주어진 유의수준에서 가능한 한 높은 검정력을 제공하므로, 최강력 검정에 가까운 성능을 보인다고 할 수 있다.

13.15 균일 최강력 검정

균일 최강력 검정(uniformly most powerful test, UMP test)은 최강력 검정의 개념을 확장한 것이다. 최강력 검정은 특정 대립가설에 대해 검정력을 최대화하는 반면, 균일 최강력 검정은 모든 가능한 대립가설에 대해 검정력을 최대화한다.

균일 최강력 검정의 정의

유의수준 \(\alpha\)에서 귀무가설 \(H_0: \theta \in \Theta_0\)에 대한 검정 \(\phi^*\)가 균일 최강력 검정이 되기 위해서는, 모든 대립가설 \(H_1: \theta \in \Theta_1\)와 모든 다른 검정 \(\phi\)에 대해 다음 조건을 만족해야 한다.

\[\beta_{\phi^*}(\theta) \geq \beta_{\phi}(\theta), \quad \forall \theta \in \Theta_1\]

여기서 \(\beta_{\phi^*}(\theta)\)와 \(\beta_{\phi}(\theta)\)는 각각 \(\phi^*\)와 \(\phi\)의 검정력 함수다.

균일 최강력 검정의 존재 조건

균일 최강력 검정이 존재하기 위해서는 몇 가지 조건이 필요하다. 카르츠-쿠른-르만 정리(Karlin-Rubin theorem)에 의해 다음과 같이 제시된다.

1. 우도비 \(\frac{L(\theta_1)}{L(\theta_0)}\)가 표본 \(X\)의 충분통계량 \(T(X)\)의 단조 증가 함수이다.
2. \(\Theta_0\)와 \(\Theta_1\)이 \(T(X)\)에 의해 분리될 수 있다. 즉, \(t\)에 대해 \(T(X) \leq t\)이면 \(\theta \in \Theta_0\)이고, \(T(X) > t\)이면 \(\theta \in \Theta_1\)이다.

이 조건들이 만족되면, 균일 최강력 검정은 다음과 같은 형태를 가진다.

\[\phi^*(x) = \begin{cases} 1, & \text{if } T(x) > c \\ \gamma, & \text{if } T(x) = c \\ 0, & \text{if } T(x) < c \end{cases}\]

\(c\)와 \(\gamma\)는 검정의 유의수준이 \(\alpha\)가 되도록 선택된다.

13.15.1 예시: 정규분포 평균에 대한 검정

정규분포 \(N(\mu, \sigma^2)\)에서 분산 \(\sigma^2\)이 알려져 있고, 평균 \(\mu\)에 대한 검정을 수행한다고 가정한다. 귀무가설과 대립가설은 다음과 같다.

• \(H_0: \mu \leq \mu_0\)
• \(H_1: \mu > \mu_0\)

표본평균 \(\bar{X}\)는 충분통계량이며, 우도비는 \(\bar{X}\)의 단조 증가 함수다. 따라서 카르츠-쿠른-르만 정리에 의해 균일 최강력 검정이 존재하며, 다음과 같이 정의된다.

\[\phi^*(x) = \begin{cases} 1, & \text{if } \bar{x} > c \\ \gamma, & \text{if } \bar{x} = c \\ 0, & \text{if } \bar{x} < c \end{cases}\]

여기서 \(c\)와 \(\gamma\)는 \(P_{\mu_0}(\bar{X} > c) + \gamma P_{\mu_0}(\bar{X} = c) = \alpha\)를 만족하도록 선택된다.

균일 최강력 검정은 모든 가능한 대립가설에 대해 검정력을 최대화하는 검정으로, 특정 조건 하에서 존재한다. 균일 최강력 검정이 존재하는 경우, 그것이 주어진 검정 문제에 대한 최선의 검정이 된다.

Fisher, R. A. (1970). Statistical methods for research workers. In Breakthroughs in statistics: Methodology and distribution (pp 66–70). Springer.

Lindquist, E. F. (1940). Statistical analysis in educational research.