8 모집단과 표본

8.1 표본추출 모의실험

극좌표계는 반지름과 각도로 점을 표현하는 좌표계다. 극좌표계를 카테시안 직교좌표계로 바꾸기 위해서 다음 수식을 이용한다. 극좌표계에서 각도와 반지름을 알면 원에 해당하는 좌표를 지정할 수 있다. 즉, 극좌표계는 각도(\(\theta\))와 반지름(\(r\))로 점의 위치를 정의한다.

X 좌표: \(x = r \times \cos(\theta)\)
Y 좌표: \(y = r \times \sin(\theta)\)

여기서, \(r\)은 원 중심으로부터 점까지 거리(반지름), \(\theta\) 는 x축과 점을 잇는 선과의 각도를 라디안 단위로 나타낸다. 예를 들어, \(r = 1\)이고 \(\theta = \frac{\pi}{4}\)인 경우, 점의 카테시안 좌표는 다음과 같다.

\[x = 1 \times \cos\left(\frac{\pi}{4}\right), \quad y = 1 \times \sin\left(\frac{\pi}{4}\right)\] \[(0.707,0.707)\]

8.1.1 모집단과 표본 추출 시각화

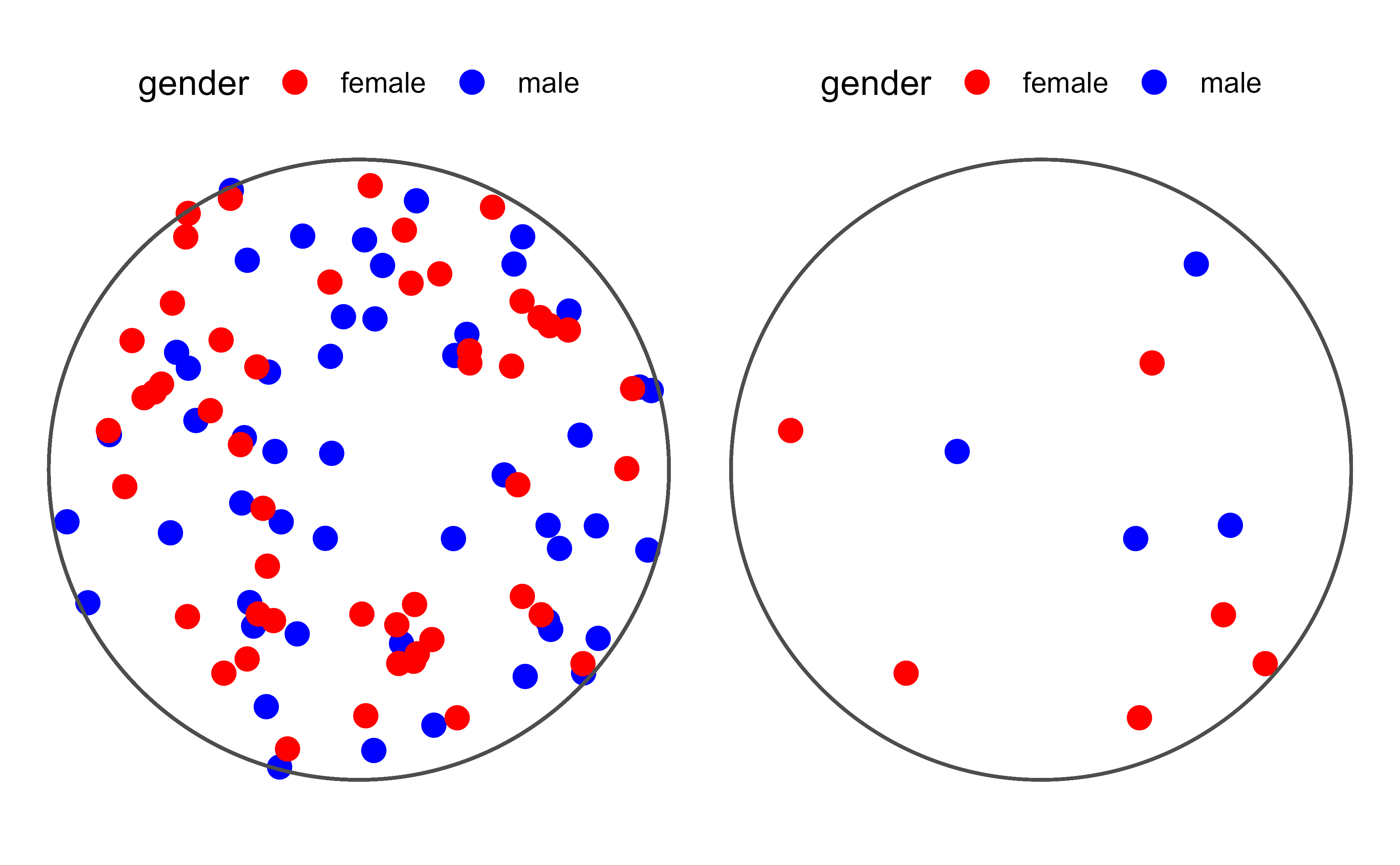
ggplot2와 ggforce 라이브러리를 사용하여 원형의 모집단을 생성하고 시각화한다. 모집단은 100명의 점들로 구성되며, 무작위로 원 안에 배치된다. 남성과 여성은 각각 50명씩 포함되어 있으며, 점의 색상으로 성별을 구분한다. 표본 추출 과정에서 모집단에서 10개의 데이터 포인트를 무작위로 선택하여 표본을 추출하여 선택된 표본이 모집단에서 어떻게 뽑혔는지 보여준다.

8.1.2 shiny 앱

#| label: fig-shiny-sampling
#| viewerHeight: 1200
#| standalone: true
library(shiny)
library(ggplot2)
library(ggforce)
library(dplyr)

ui <- fluidPage(
  titlePanel("모집단에서 표본 추출"),
  sidebarLayout(
    sidebarPanel(
      sliderInput("sample_size", "표본 크기", min = 1, max = 100, value = 10),
      verbatimTextOutput("sample_summary")
    ),
    mainPanel(
      plotOutput("population_plot"),
      plotOutput("sample_plot")
    )
  )
)

server <- function(input, output) {
  set.seed(123)
  n <- 100
  angles <- runif(n, 0, 2*pi)
  radii <- sqrt(runif(n, 0, 1))
  x <- radii * cos(angles)
  y <- radii * sin(angles)
  population <- tibble(x = x, y = y) %>%
    mutate(gender = c(rep("남자", 50), rep("여자", 50)))

  output$population_plot <- renderPlot({
    ggplot(population) +
      geom_point(aes(x, y, color = gender), size = 3) +
      geom_circle(aes(x0 = 0, y0 = 0, r = 1), color = "gray30") +
      theme_void() +
      scale_color_manual(values = c("여자" = "red", "남자" = "blue")) +
      theme(legend.position = "top") +
      coord_fixed() +
      labs(title = "모집단", color = "성별")
  })

  sample <- reactive({
    population %>%
      sample_n(input$sample_size, replace = FALSE)
  })

  output$sample_plot <- renderPlot({
    ggplot(sample()) +
      geom_point(aes(x, y, color = gender), size = 3) +
      geom_circle(aes(x0 = 0, y0 = 0, r = 1), color = "gray30") +
      theme_void() +
      scale_color_manual(values = c("여자" = "red", "남자" = "blue")) +
      theme(legend.position = "top") +
      coord_fixed() +
      labs(title = "추출된 표본", color = "성별")
  })

  output$sample_summary <- renderText({
    male_count <- sum(sample()$gender == "남자")
    female_count <- sum(sample()$gender == "여자")
    paste("추출된 표본 요약:\n",
          "남자:", male_count, "명\n",
          "여자:", female_count, "명")
  })
}

shinyApp(ui, server)

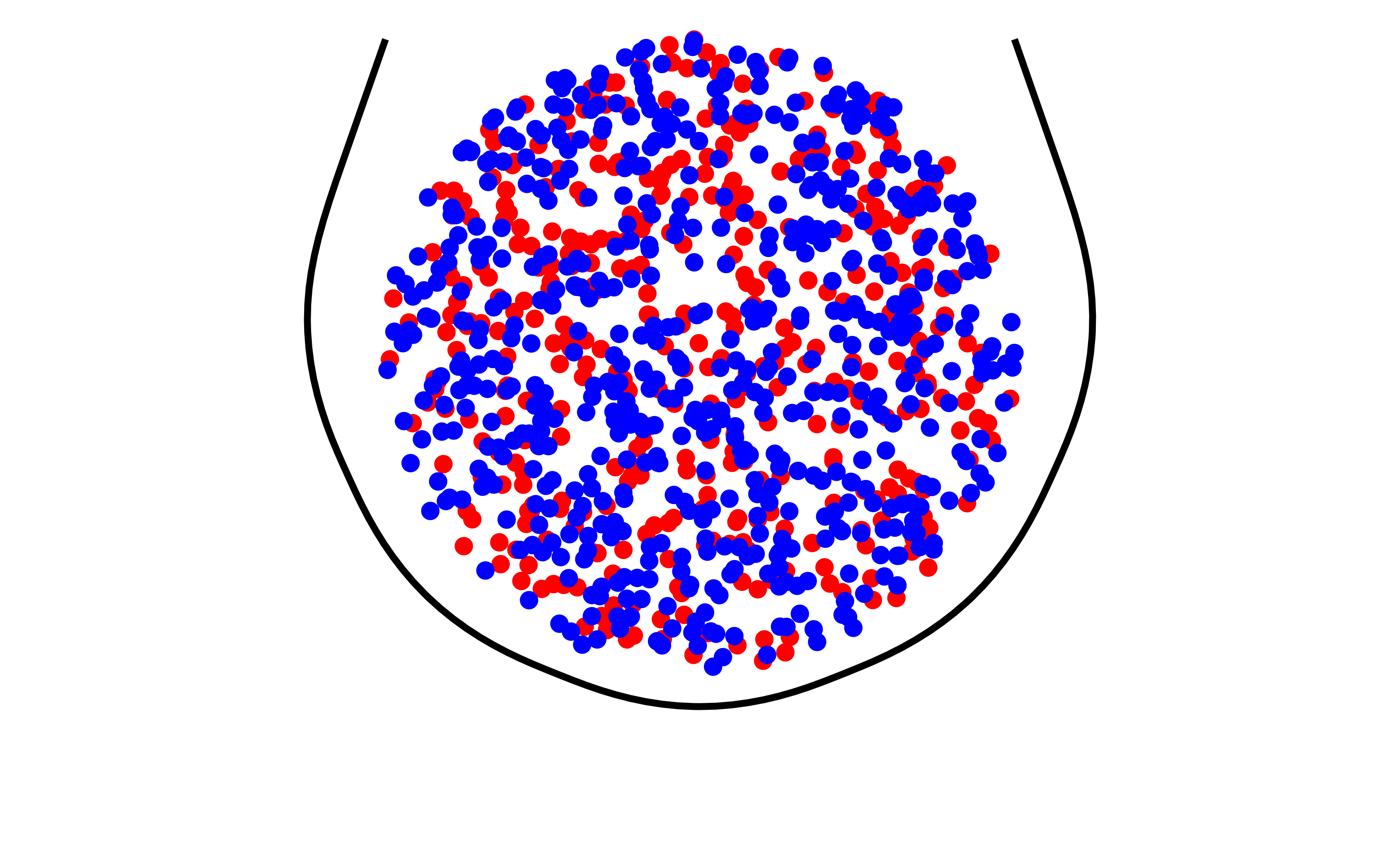
표본 추출은 통계학에서 중요한 개념으로 모집단에서 일부 데이터를 추출하는 과정을 의미한다. 이를 통해 모집단의 특성을 추정하거나 가설 검정을 수행할 수 있다. 다음과 같이 항아리속에 빨간공과 파란공이 섞여 있는 상황을 가정해보자. 이때, 항아리속의 공을 무작위로 추출하여 파란공의 색상을 확인하는 과정을 표본 추출로 볼 수 있다. 즉, 항아리속 일부 공을 무작위로 추출하여 파란공의 비율이 얼마인지 추정하는 것이다.

8.2 항아리속 파란 공

모집단은 연구 대상 전체를 의미하며, 표본은 모집단에서 추출한 일부 데이터를 의미한다. 여기서, 항아리 속 공은 모집단으로 볼 수 있고 모집단에서 추출한 공은 표본으로 볼 수 있다. 무작위로 항아리 속에 손을 넣어 공을 추출하는 과정을 표본 추출로 볼 수 있다.

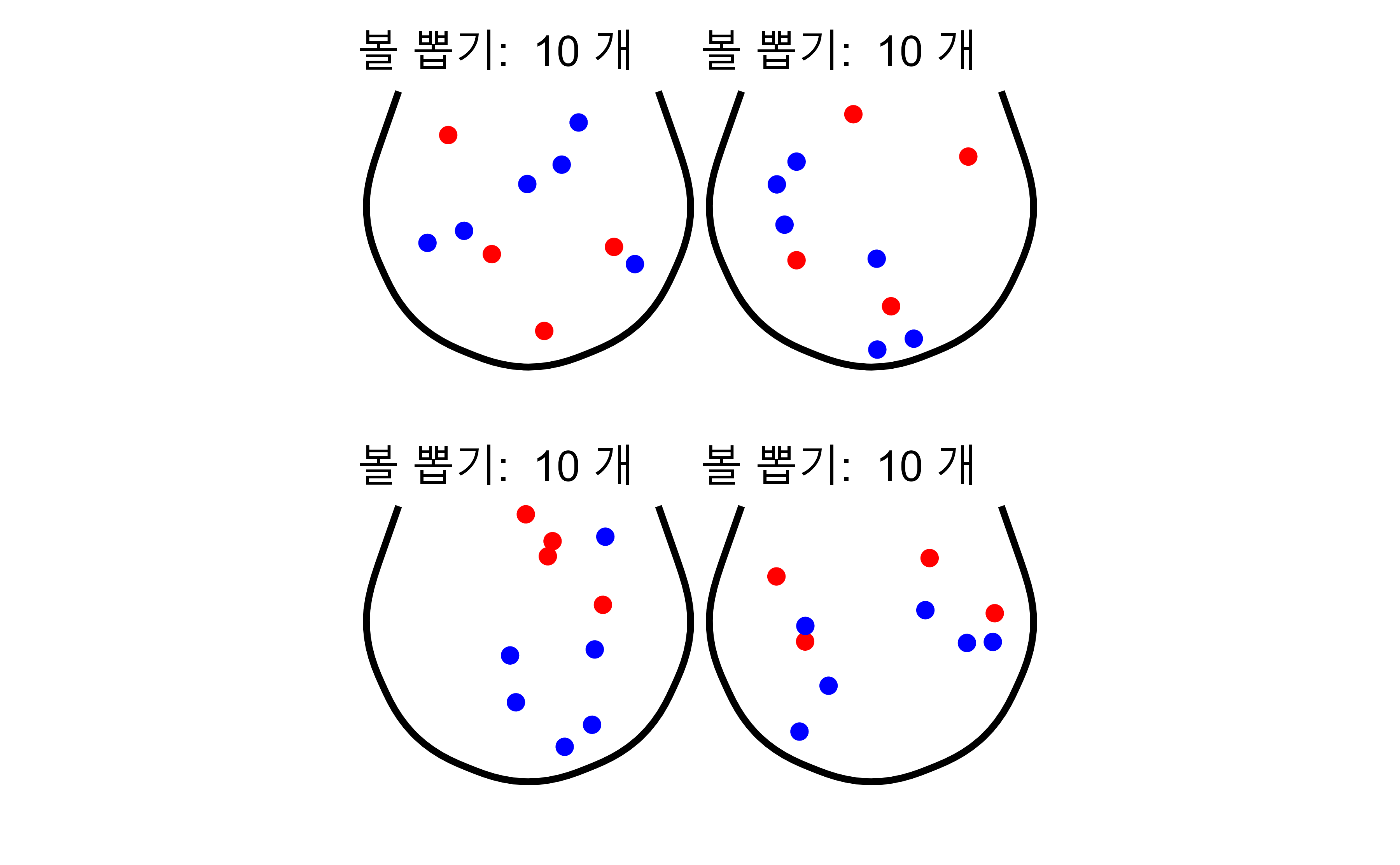
항아리에서 공을 10개 추출할 수도 있고 100개 추출할 수도 있다. 또한, 공을 10개 추출하는 행위를 5번 반복할 수도 있고 100개 추출하는 행위를 5번 반복할 수도 있다.

먼저 볼을 무작위로 10개 뽑는데 이 과정을 4회 반복하는 과정을 시각적으로 표현하면 다음과 같다.

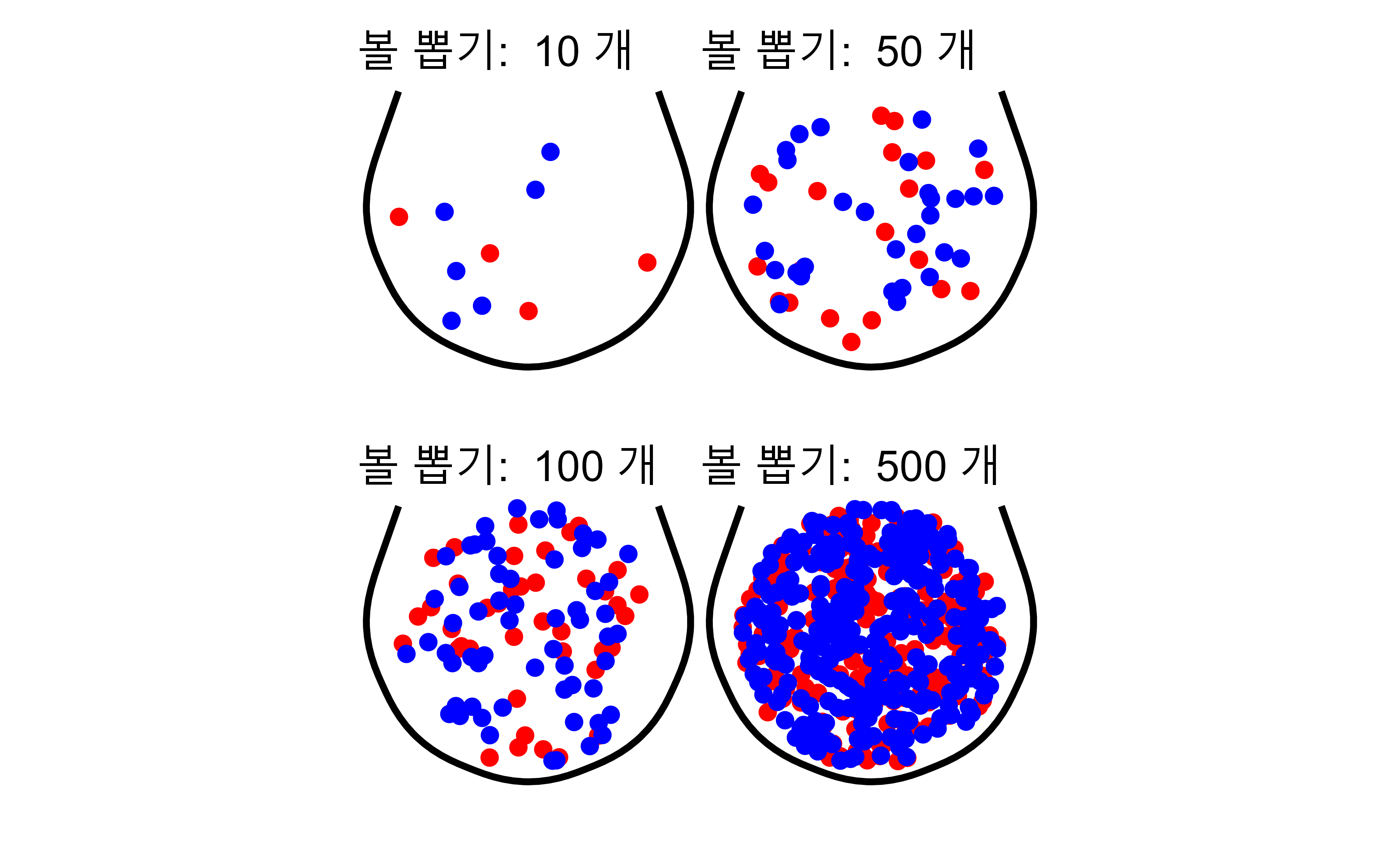
이번에는 추출하는 볼 갯수를 달리하여 볼을 무작위로 10, 50, 100, 500개 추출하는 과정을 시각화해보면 다음과 같다.

8.3 추정

항아리속에 빨간공과 파란공이 섞여 있는 상황에서 무작위로 추출한 볼의 색상을 확인하는 과정을 표본 추출 과정이고 추출된 표본을 통해 모집단의 특성을 추정하는 것을 추정이라고 한다. 관심있는 것은 파란색 공의 비율을 추정해보자.

#> # A tibble: 2 × 4
#> # Groups:   replicate [1]
#>   replicate color  볼수  비율
#>       <int> <chr> <int> <dbl>
#> 1         1 blue      7   0.7
#> 2         1 red       3   0.3

moderndive 패키지를 사용해 파란색 공의 비율을 추정해보자. 먼저 rep_sample_n() 함수로 볼을 10개 추출한 후 파란색 공의 비율을 계산해보자. 표본 10개를 표본크기 size 인자로 추출한다. count() 함수와 mutate() 함수로 항아리 속 파란색 공의 비율을 계산할 수 있다. 파란색 공의 비율은 파란색 공의 개수를 전체 공의 개수로 나눈 값으로 70%가 나왔다.

#> # A tibble: 30 × 2
#>   replicate  비율
#>       <int> <dbl>
#> 1         1   0.7
#> 2         2   0.7
#> 3         3   0.4
#> 4         4   0.6
#> 5         5   0.6
#> 6         6   0.5
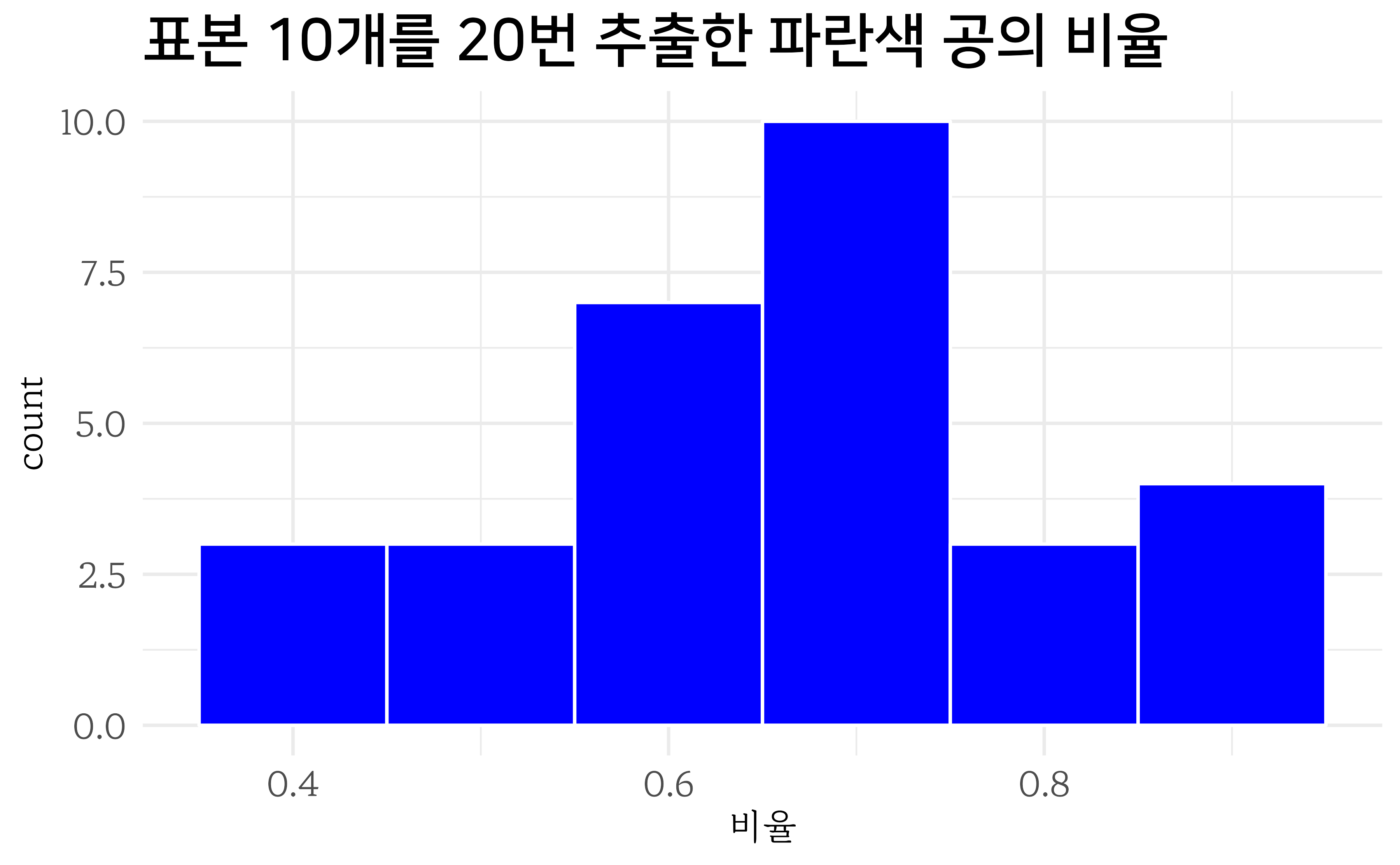
#> # ℹ 24 more rows

이번에는 10개의 볼을 30번 추출한 후 파란색 공의 비율을 계산해보자. rep_sample_n() 함수의 reps 인자로 표본 추출을 반복할 횟수를 지정할 수 있다. R에서 TRUE는 1, FALSE는 0으로 취급되므로 mean() 함수로 파란색 공의 비율을 계산할 수 있다. 이를 위해 먼저 mutate() 함수로 파란색 공인지 아닌지를 확인하는 변수를 만들어주고 group_by() 함수로 표본 추출을 반복한 횟수로 그룹을 나누어 summarise() 함수로 파란색 공의 비율을 계산할 수 있다. 표본을 추출할 때마다 파란색 공의 비율이 다르게 나타난다.

10개의 볼을 30번 추출한 후 파란색 공의 비율을 히스토그램으로 시각화해보자. geom_histogram() 함수의 binwidth 인자로 막대의 너비를 지정할 수 있다.

8.4 반복횟수 증가

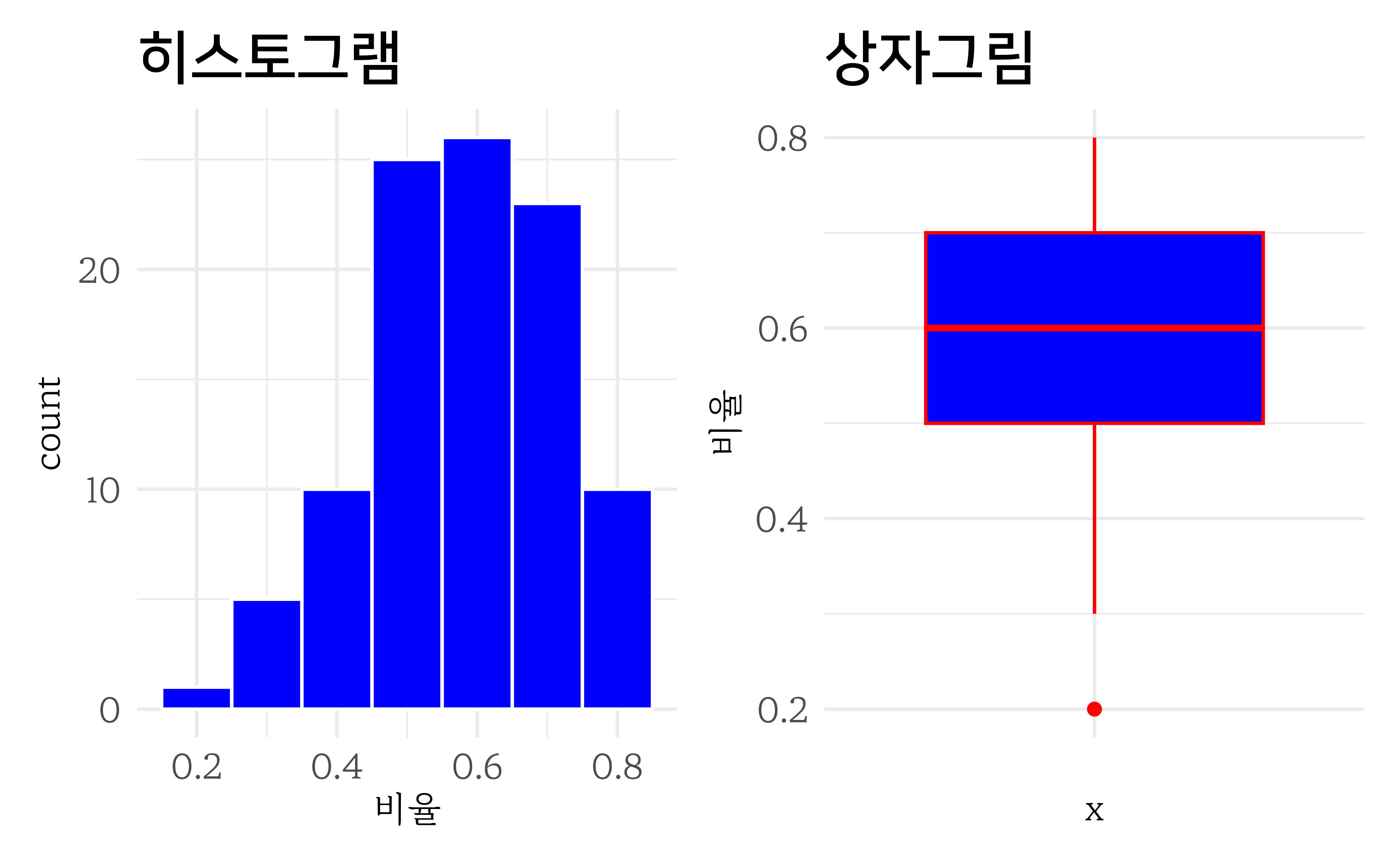
10개의 볼을 뽑는 반복횟수를 30번이 아니고 100번과 1,000번으로 증가시켜보자. 먼저, 10개의 볼을 뽑았을 때 파란공의 비율을 계산하여 요약통계량을 계산해보자. 대략 40% 비율로 파란공이 추출되었으나 파란공이 매우 적게 추출된 경우와, 파란공이 매우 많이 추출된 경우도 있다.

#> # A tibble: 1 × 5
#>   최소값  평균 최대값   분산 표준편차
#>    <dbl> <dbl>  <dbl>  <dbl>    <dbl>
#> 1    0.2 0.579    0.8 0.0186    0.137

히스토그램과 상자그림을 그려보면 다음과 같다.

8.5 표본크기 증가

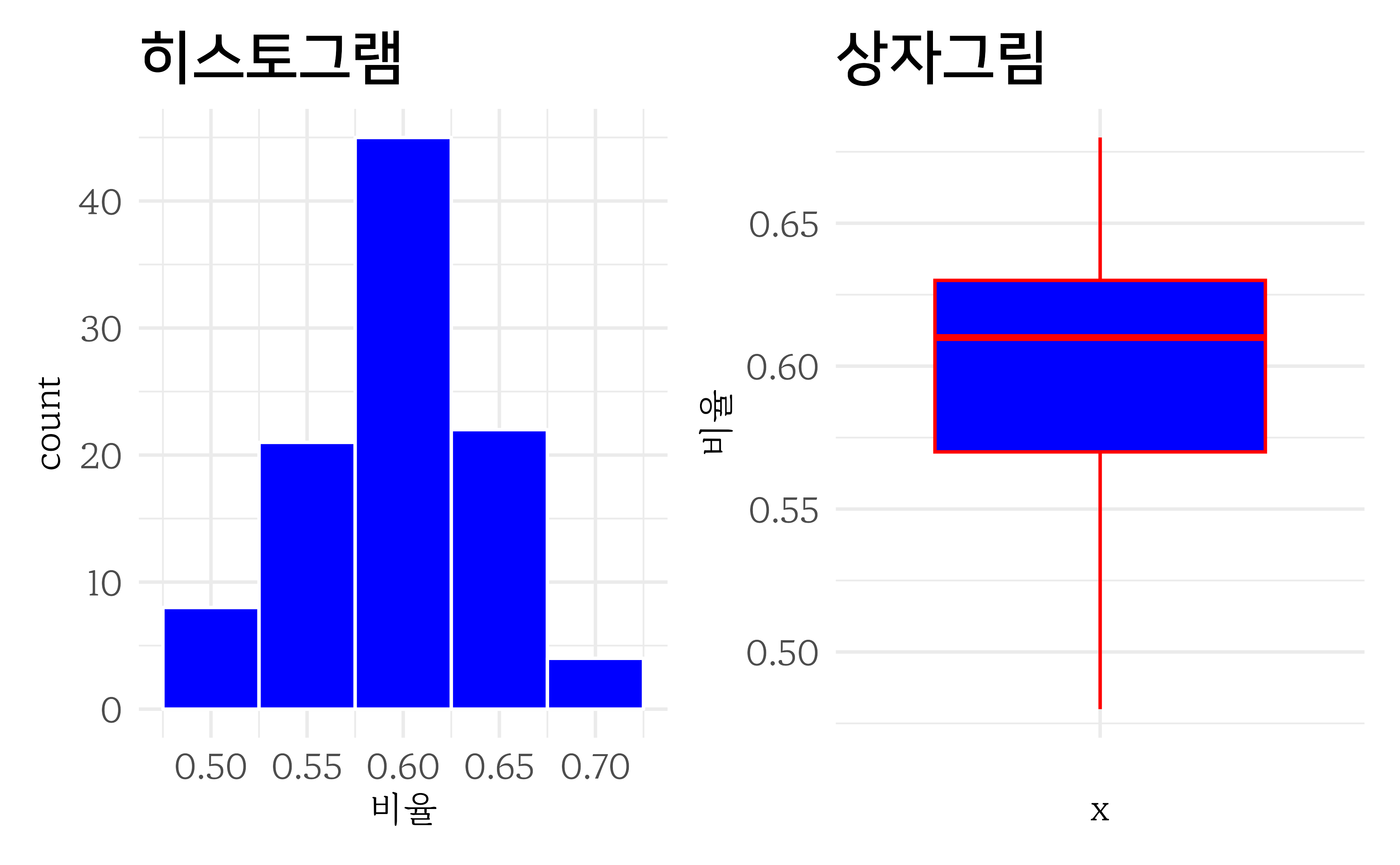
표본크기로 10개의 볼을 뽑는 대신 100개 볼을 반복해서 100번 뽑아보자.

#> # A tibble: 1 × 5
#>   최소값  평균 최대값    분산 표준편차
#>    <dbl> <dbl>  <dbl>   <dbl>    <dbl>
#> 1   0.48 0.598   0.68 0.00213   0.0461

히스토그램과 상자그림을 그려보면 다음과 같다.

8.6 대수의 법칙

대수의 법칙(Law of Large Numbers, LLN)은 확률론에서 중요한 정리 중 하나다. 대수의 법칙은 큰 수의 약한 법칙(Weak Law of Large Numbers)과 큰 수의 강한 법칙(Strong Law of Large Numbers)으로 나눠진다.

큰 수의 약한 법칙(Weak Law of Large Numbers)

동일한 확률 분포를 가지고, 서로 독립적인 확률 변수들 \(X_1, X_2, \ldots, X_n\)에 대해 적용된다. 각 확률 변수의 기대값이 \(E(X_i) = \mu\) (모든 \(i\)에 대해 동일)라고 가정할 때, 표본 평균 \(\bar{X}_n = \frac{1}{n}(X_1 + X_2 + \ldots + X_n)\)은 \(n\)이 증가함에 따라 모평균 \(\mu\)에 확률적으로 수렴한다. 수식으로 표현하면 다음과 같다.

\[ P\left(\lim_{n \to \infty} |\bar{X}_n - \mu| = 0\right) = 1 \]

여기서 \(P\)는 확률을 의미하며, \(n\)이 무한대로 갈수록 표본 평균 \(\bar{X}_n\)이 모평균 \(\mu\)에 가까워진다는 것을 의미한다.

큰 수의 강한 법칙(Strong Law of Large Numbers)

큰 수의 강한 법칙은 약한 법칙보다 더 엄격한 조건을 제시한다. 동일하게 분포하고 서로 독립적인 확률 변수들 \(X_1, X_2, \ldots, X_n\)에 대해 적용되며, 각 확률 변수의 기대값이 \(E(X_i) = \mu\) 일 때, 표본 평균 \(\bar{X}_n\)이 모평균 \(\mu\)에 거의 확실하게(즉, 확률 1로) 수렴한다. 확률 변수의 수 \(n\)이 무한대로 갈수록 표본 평균이 모평균에 수렴한다는 것을 의미한다. 수학적으로 다음과 같이 표현할 수 있다.

\[ P\left(\lim_{n \to \infty} \bar{X}_n = \mu\right) = 1 \]

\(P\)는 확률을 의미한다. 강한 법칙은 거의 모든 표본 경로(sample path)에서 표본 평균이 모평균에 수렴함을 보장한다. 즉, 무한히 많은 시행에서 표본 평균은 거의 확실하게 모평균에 수렴하게 된다.

큰 수의 약한 법칙과 큰 수의 강한 법칙의 차이는 수렴의 확실성의 정도에 있다. 약한 법칙은 표본 평균이 모평균에 확률적으로 수렴한다고 말하는 반면, 강한 법칙은 이 수렴이 거의 확실하게 일어난다고 말하고 있다.

8.7 shiny 앱

#| label: shinylive-balls-lln
#| viewerHeight: 600
#| standalone: true
library(shiny)
library(ggplot2)
library(dplyr)
library(moderndive)
library(patchwork)

ui <- fluidPage(
  titlePanel("대수의 법칙 시각화"),

  sidebarLayout(
    sidebarPanel(
      h3("설명"),
      p("표본 추출과 대수의 법칙을 시각화하는 앱입니다."),
      p("모집단에서 표본을 반복적으로 추출하여 파란색 공의 비율을 계산합니다."),
      p("파란색 공의 비율, 표본 크기, 반복 횟수를 조정하여 대수의 법칙을 확인할 수 있습니다."),

      h4("모수 설정"),
      sliderInput("blue_prop", "파란색 공의 비율:", min = 0.1, max = 0.9, value = 0.6, step = 0.1),
      hr(),
      h4("표본 크기와 반복 횟수"),
      sliderInput("sample_size", "표본 크기:", min = 10, max = 500, value = 100),
      sliderInput("num_reps", "반복 횟수:", min = 10, max = 1000, value = 100)
    ),

    mainPanel(
      plotOutput("combined_plot"),
      verbatimTextOutput("summary_stats")
    )
  )
)

server <- function(input, output) {

  balls <- reactive({
    red_prop <- 1 - input$blue_prop
    positions <- tibble(
      x = runif(1000, -1, 1),
      y = runif(1000, -1, 1),
      color = c(rep("red", round(1000 * red_prop)), rep("blue", round(1000 * input$blue_prop)))
    )

    positions %>%
      rep_sample_n(size = input$sample_size, reps = input$num_reps) %>%
      mutate(is_blue = color == "blue") %>%
      group_by(replicate) %>%
      summarise(비율 = mean(is_blue)) %>%
      ungroup()
  })

  output$combined_plot <- renderPlot({
    hist_plot <- balls() %>%
      ggplot(aes(x = 비율)) +
      geom_histogram(binwidth = 0.05, fill = "blue") +
      labs(title = "파란색 공의 비율 히스토그램", x = "비율", y = "빈도")

    box_plot <- balls() %>%
      ggplot(aes(x = "", y = 비율)) +
      geom_boxplot(fill = "blue") +
      labs(title = "파란색 공의 비율 상자그림", x = "", y = "비율")

    hist_plot + box_plot
  })

  output$summary_stats <- renderPrint({
    balls() %>%
      summarise(
        최소값 = min(비율),
        평균 = mean(비율),
        최대값 = max(비율),
        분산  = var(비율),
        표준편차 = sd(비율)
      )
  })
}

shinyApp(ui, server)