21  베이즈 정리

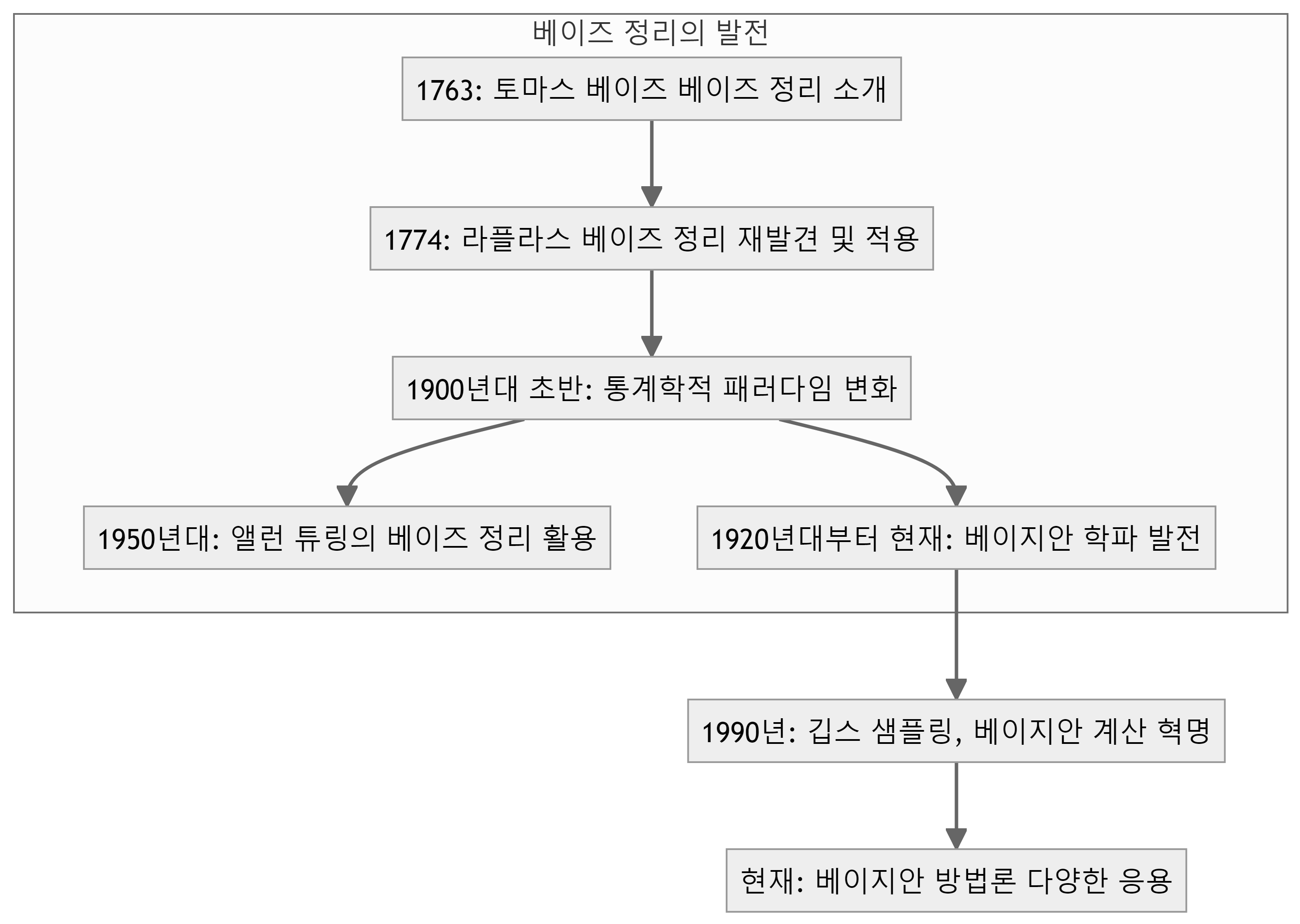
토마스 베이즈(Thomas Bayes, 1701-1761)는 영국의 목사이자 수학자로 알려져 있으며 주로 확률론에 기여했다. 생전에 자신의 연구 결과를 출판하지 않았고, 사후에 친구 리처드 프라이스(Richard Price)에 의해 베이즈의 저작이 출판되었다. 베이즈 정리는 사후 출판된 논문 “An Essay towards solving a Problem in the Doctrine of Chances”(Bayes, 1763)에서 처음 소개되었다.

흥미로운 사실은 베이즈가 생전에는 수학자로서 크게 주목받지 못했다는 점이다. 그의 업적(이재용·이경재·이영선, 2014)은 사후에 알려지게 되었고, 20세기 초반에 들어서야 통계학자들에 의해 재발견되었다.

1774년에는 피에르 시몽 라플라스가 베이즈 정리를 재발견하고 이를 다양한 분야에 적용하였으며, 균등분포를 사전분포로 사용하는 근거를 마련하였고, 1900년대 초반에는 피셔, 네이만, 피어슨 등에 의해 빈도론적 통계학이 발전하면서 베이지안 통계학은 침체기를 겪었나 1950년대에는 앨런 튜링 등이 실질적인 문제 해결에 베이즈 정리를 활용하였다.

1920년대부터 현재까지 주관적 베이지안과 객관적 베이지안 학파가 각각 발전해 왔다. 주관적 베이지안은 램지, 드 피네티, 새비지 등에 의해 발전되었고, 객관적 베이지안은 제프리스, 제인스, 린들리 등에 의해 발전되었다.

1990년에는 겔판드와 스미스가 깁스 샘플링을 소개하면서 베이지안 계산에 혁명적인 발전이 이루어졌다. 이를 계기로 베이지안 통계학이 다시 부흥하게 되었다.

베이즈 정리는 250여 년의 역사 동안 빈도론적 통계학에 밀려 침체기를 겪기도 했지만, 20세기 후반 들어 계산 기술의 발달과 함께 다시 주목받게 되었다. 최근에는 스팸 메일 필터링, 음성 인식, 자연어 처리 등 다양한 분야에서 베이즈 정리가 활용되고 있다. 구글, 마이크로소프트, 애플 등 대형 IT 기업들은 베이즈 정리를 바탕으로 한 기계 학습 알고리즘을 활용하여 사용자 경험을 개선하고 있다.

그림 21.1: 베이즈 정리 발전과정

21.1 수식

베이즈 정리는 두 사건 간의 관계를 조건부 확률로 나타내며, 새로운 정보나 증거가 주어졌을 때 이를 반영하여 확률을 갱신하는데 사용된다. 베이즈 정리는 사전확률과 우도를 결합하여 사후확률을 계산하는 데 사용되며, 통계학, 기계학습, 데이터 분석 등 다양한 분야에서 활용되며, 불확실성을 다루는 데 핵심적인 역할을 한다.

\[P(A|B) = \frac{P(B|A)P(A)}{P(B)}\]

• \(P(A|B)\): 사건 B가 주어졌을 때 사건 A의 조건부 확률 (사후확률)
• \(P(B|A)\): 사건 A가 주어졌을 때 사건 B의 조건부 확률 (우도)
• \(P(A)\): 사건 A의 사전확률
• \(P(B)\): 사건 B의 주변확률 (evidence)

사건 B의 주변확률 \(P(B)\)는 전확률의 법칙(Law of Total Probability)을 이용하여 다음과 같이 계산할 수 있다.

\[P(B) = \sum_{i=1}^{n} P(B|A_i)P(A_i)\]

\(A_1, A_2, ..., A_n\)은 서로 배반하고 전체 사건의 합집합은 표본공간이 되는 사건들이다.

일상에서 날씨와 관련된 간단한 예시를 통해 베이즈 정리를 살펴보자. 어떤 도시에서 비가 올 확률은 30%이고, 비가 올 때 우산을 가지고 있을 확률은 60%, 비가 오지 않을 때 우산을 가지고 있을 확률은 20%라고 가정해본다.

어떤 사람이 우산을 가지고 있다는 사실이 관측되었을 때, 실제로 비가 올 확률을 베이즈 정리를 사용하여 계산해본다.

• 사건 \(A\): 비가 옴
• 사건 \(B\): 우산을 가지고 있음

먼저 앞서 기술된 사항을 수식으로 표현해보면 다음과 같다.

\(P(A) = 0.3\) (비가 올 확률)
\(P(B|A) = 0.6\) (비가 올 때 우산을 가질 확률)
\(P(B|\neg A) = 0.2\) (비가 오지 않을 때 우산을 가질 확률)
\(P(B) = P(B|A)P(A) + P(B|\neg A)P(\neg A)\) (전확률의 법칙에 의해 계산) 베이즈 정리에 대입하면

\[ \begin{align*} P(A|B) &= \frac{P(B|A)P(A)}{P(B|A)P(A) + P(B|\neg A)P(\neg A)} \\ &= \frac{0.6 \times 0.3}{0.6 \times 0.3 + 0.2 \times 0.7} \\ &= \frac{0.18}{0.18 + 0.14} \\ &= \frac{0.18}{0.32} \approx 0.5625 \end{align*} \]

따라서 우산을 가지고 있는 사람이 관측되었을 때, 실제로 비가 올 확률은 약 56.25%이다. 베이즈 정리는 관측된 증거(우산을 가지고 있음)를 바탕으로 원인(비가 옴)의 확률을 추론하는 데 사용된다.

21.2 R 코드

#> * 비가 올 사전확률: 0.3
#> * 비가 오지 않을 사전확률: 0.7
#> * 우산을 가질 전확률: 0.32
#> * 비가 올 때 우산을 가질 우도: 0.6
#> * 비가 오지 않을 때 우산을 가질 우도: 0.2
#> ==> 우산을 가지고 있을 때 비가 올 사후확률: 0.5625

#> # A tibble: 2 × 5
#>   hypothesis umbrella prob.x prob.y posterior
#>   <chr>      <chr>     <dbl>  <dbl>     <dbl>
#> 1 rain       umbrella    0.6    0.3     0.563
#> 2 no_rain    umbrella    0.2    0.7     0.438

21.3 조건부 확률과 독립성

조건부 확률(conditional probability)은 다른 사건이 일어났다는 정보가 주어졌을 때, 어떤 사건이 일어날 확률을 의미한다. 조건부 확률은 두 사건의 관계를 이해하고 분석하는 데 중요한 개념이다.

두 사건 A와 B에 대해, 사건 B가 일어났다는 조건 하에서 사건 A가 일어날 조건부 확률은 다음과 같이 정의된다.

\(P(A|B) = \frac{P(A \cap B)}{P(B)}\), 단 \(P(B) > 0\)

여기서 \(P(A \cap B)\)는 사건 A와 B가 동시에 일어날 확률, 즉 교집합의 확률을 나타낸다.

조건부 확률은 다음과 같은 성질을 가진다.

1. 조건부 확률 범위 - \(0 \leq P(A|B) \leq 1\)
2. 곱셈법칙 - \(P(A \cap B) = P(A|B)P(B) = P(B|A)P(A)\)
3. 조건부 확률 덧셈법칙 - \(P(A_1 \cup A_2|B) = P(A_1|B) + P(A_2|B) - P(A_1 \cap A_2|B)\)

두 사건 A와 B가 독립(independent)이라는 것은 한 사건의 발생 여부가 다른 사건의 발생 여부에 영향을 미치지 않는 것을 의미한다. 수학적으로는 다음과 같이 정의된다.

\(P(A \cap B) = P(A)P(B)\)

또는 등가적으로,

\(P(A|B) = P(A)\) 또는 \(P(B|A) = P(B)\), 단 \(P(B) > 0, P(A) > 0\)

즉, 두 사건 A와 B가 독립이면 조건부 확률 \(P(A|B)\)는 사건 A의 확률 \(P(A)\)와 같다.

21.4 사례

의료 진단에서 조건부 확률을 활용하는 것은 매우 중요하다. 이를 통해 의사는 검사 결과를 해석하고 진단의 정확성을 평가할 수 있기 때문이다. 실제로 의료 현장에서는 검사의 민감도와 특이도를 고려하여 질병의 진단 확률을 계산하고 있다.

예를 들어, 국민건강통계에 따르면 2021년 남녀가 차이가 있지만 대략 10%가 당뇨병에 걸려 있다고 한다. 질병을 진단하는 검사의 민감도(당뇨병이 있을 때 검사가 양성일 확률)는 90%, 특이도(당뇨병이 없을 때 검사가 음성일 확률)는 95%라고 하자. 검사 결과가 양성인 사람이 실제로 당뇨병을 가지고 있을 확률은 얼마일까?

• 사건 \(A\): 당뇨병에 걸림 (10%)
• 사건 \(B\): 검사 결과 양성
• 민감도 \(P(B|A) = 0.9\), 특이도 \(P(B^c|A^c) = 0.95\)

베이즈 정리를 활용하여 구하고자 하는 확률은 \(P(A|B)\)을 계산할 수 있다.

\[ \begin{align*} P(A|B) &= \frac{P(B|A)P(A)}{P(B)} \\ &= \frac{P(B|A)P(A)}{P(B|A)P(A) + P(B|A^c)P(A^c)} \\ &= \frac{0.9 \times 0.1}{0.9 \times 0.1 + 0.05 \times 0.9} \\ &= \frac{0.09}{0.09 + 0.045} = \frac{0.09}{0.135} = 0.6667 \end{align*} \]

즉, 검사 결과가 양성인 사람 중 실제로 당뇨병을 가지고 있을 확률은 약 66.67%이다. R 코드로 확인하면 다음과 같다.

사전 확률(당뇨병 유병률)이 10%로 상대적으로 높기 때문에, 검사 결과가 양성일 때 실제로 당뇨병을 가지고 있을 확률이 66.67%로 비교적 높게 나타난다. 하지만 검사의 민감도와 특이도, 그리고 질병의 유병률에 따라 달라질 수 있다.

21.5 shiny 앱

#| label: shinylive-bayes-diabetes
#| viewerHeight: 600
#| standalone: true
library(shiny)

ui <- fluidPage(
  titlePanel("당뇨병 검사 결과 해석기"),

  sidebarLayout(
    sidebarPanel(
      h3("설명"),
      p("당뇨병 검사 결과를 해석하는데 도움을 줍니다."),
      p("사용자가 당뇨병의 유병률 P(A), 검사의 민감도 P(B|A) 와 특이도 P(B^c|A^c)를 입력하면,"),
      p("검사 결과가 양성일 때 실제로 당뇨병을 가지고 있을 확률 P(A|B)을 계산합니다."),
      p("이를 통해 검사 결과를 보다 정확하게 해석할 수 있습니다."),
      br(),
      sliderInput("prevalence", "유병률 P(A) (%):", min = 0, max = 100, value = 10),
      sliderInput("sensitivity", "민감도 P(B|A) (%):", min = 0, max = 100, value = 90),
      sliderInput("specificity", "특이도 P(B^c|A^c) (%):", min = 0, max = 100, value = 95)
    ),

    mainPanel(
      h3("계산 과정"),
      uiOutput("calculation"),
      br(),
      h3("검사 결과가 양성일 때 실제 당뇨병을 가지고 있을 확률 (P(A|B))"),
      verbatimTextOutput("result")
    )
  )
)

server <- function(input, output) {

  # 확률 계산 함수
  calculate_probability <- reactive({
    prevalence <- input$prevalence / 100
    sensitivity <- input$sensitivity / 100
    specificity <- input$specificity / 100

    p_A_given_B <- (sensitivity * prevalence) / (sensitivity * prevalence + (1 - specificity) * (1 - prevalence))

    return(round(p_A_given_B, 4))
  })

  # 결과 출력
  output$result <- renderText({
    paste0(calculate_probability() * 100, "%")
  })

  # 계산 과정 출력
  output$calculation <- renderUI({
    prevalence <- input$prevalence / 100
    sensitivity <- input$sensitivity / 100
    specificity <- input$specificity / 100

    withMathJax(
      helpText("$$P(A|B) = \\frac{P(B|A)P(A)}{P(B)}$$"),
      helpText("$$= \\frac{P(B|A)P(A)}{P(B|A)P(A) + P(B|A^c)P(A^c)}$$"),
      helpText(sprintf("$$= \\frac{%.2f \\times %.2f}{%.2f \\times %.2f + %.2f \\times %.2f}$$",
                       sensitivity, prevalence, sensitivity, prevalence, 1 - specificity, 1 - prevalence)),
      helpText(sprintf("$$= \\frac{%.4f}{%.4f + %.4f} = %.4f$$",
                       sensitivity * prevalence, sensitivity * prevalence, (1 - specificity) * (1 - prevalence),
                       calculate_probability()))
    )
  })
}

shinyApp(ui = ui, server = server)

그림 21.1: 베이즈 정리 발전과정

Bayes, T. (1763). LII. An essay towards solving a problem in the doctrine of chances. By the late Rev. Mr. Bayes, FRS communicated by Mr. Price, in a letter to John Canton, AMFR S. Philosophical transactions of the Royal Society of London, 53, 370–418.

이재용·이경재·이영선. (2014). 베이지안 통계의 역사와 미래에 대한 조망. 응용통계연구.