13 많은 회귀모형

많은 회귀모형(Many models)은 데이터 과학에서 흔히 관찰되는 다양한 소그룹이나 개별 요소에 대해 단순한 모형을 독립적으로 적용하는 데이터 분석 방식이다. 복잡한 데이터셋 내에서 각 세부 요소를 분석함으로써 전체 데이터의 이해도를 높이는 데 도움이 되고, 각 모형을 통해 특정 그룹이나 요소의 고유한 특성과 변동성을 파악할 수 있어 데이터 내 숨겨진 패턴이나 관계를 발견할 수 있다. 예를 들어, 시도 단위로 나뉜 행정구역 데이터의 숨겨진 패턴과 관계를 시도 단위로 나누고 단순한 회귀모형을 적합시켜 회귀모형에 담긴 정보를 broom 패키지를 통해 추출하여 시각화하거나 요약통계량을 구함으로써 다른 모형으로는 찾기 어려운 시도별 숨겨진 패턴을 발견할 수 있고 리스트 칼럼(list column) 자료형으로 수월한 커뮤니케이션도 가능하다.

13.0.1 기대수명 데이터

many models를 적용할 수 있는 데이터는 흔히 주변에서 찾을 수 있다. 여기서는 gapminder 데이터셋을 사용하여 다양한 국가별 기대수명 데이터를 활용하여 회귀모형을 구축하고 시각화하는 방법을 알아본다. gapminder 데이터를 가지고 회귀모형을 구축하고 모형을 활용하여 종속변수(기대수명, lifeExp)가 늘어나지 못한 국가를 찾아내고 어떠한 특징을 가지고 있는지 broom 패키지로 회귀모형 결과를 다시 데이터프레임으로 구축한 후 결정계수 \(R^2\) 혹은 AIC/BIC/SBC와 같은 통계량을 통해 걸러낸 후 커뮤니케이션을 위해 시각화하는 방법을 살펴보자.

# 0. 환경설정 -----
library(gapminder) # 데이터
library(tidyverse) # Tidyverse
library(broom)     # 모형

# 1. 데이터 -----
gapminder
#> # A tibble: 1,704 × 6
#>   country     continent  year lifeExp      pop gdpPercap
#>   <fct>       <fct>     <int>   <dbl>    <int>     <dbl>
#> 1 Afghanistan Asia       1952    28.8  8425333      779.
#> 2 Afghanistan Asia       1957    30.3  9240934      821.
#> 3 Afghanistan Asia       1962    32.0 10267083      853.
#> 4 Afghanistan Asia       1967    34.0 11537966      836.
#> 5 Afghanistan Asia       1972    36.1 13079460      740.
#> 6 Afghanistan Asia       1977    38.4 14880372      786.
#> # ℹ 1,698 more rows

Gapminder 데이터셋(로슬링 2019)은 전 세계 국가들의 건강, 교육, 경제 등 다양한 지표에 관한 통계 데이터를 연도별로 제공하여 국가 간 발전 격차와 시간에 따른 변화 정보를 담고 있다. 한스 로슬링의 TED 강연을 통해 대중들의 국가 간 격차와 발전에 대한 인식을 변화시켰을 뿐만 아니라, 혁신적인 데이터 시각화 기법을 사용하여 데이터 시각화 분야의 발전에 영감을 주었으며, 학생들과 연구자들에게 실제 데이터를 활용한 분석 및 시각화 연습의 기회를 제공하고 있다. 제니 브라이언이 만든 gapminer 데이터 패키지는 gapminder 데이터셋을 R에서 쉽게 활용할 수 있도록 제공되어 gganimate, ggplot 등 다양한 R 패키지와 결합하여 펭귄 데이터와 함께 데이터 과학의 기본 데이터로 자리매김하고 있다.

13.0.2 기대수명 회귀분석

대륙과 국가를 그룹으로 잡아 회귀분석을 각각에 대해서 돌리고 나서, 모형 결과값을 데이터와 모형이 함께 위치하도록 티블(tibble)에 저장시켜 놓는다. 그리고 나서, 주요한 회귀모형 성능지표인 결정계수(\(R^2\))를 기준으로 정렬시킨다.

# 2. 모형 -----
country_model <- function(df)
  lm(lifeExp ~ year, data=df)

by_country <- gapminder %>% 
  group_by(country, continent) %>% 
  nest() %>% 
  mutate(model = map(data, country_model),
         model_glance = map(model, glance),
         rsquare = map_dbl(model_glance, ~.$r.squared)) |> 
  ungroup()

by_country %>% 
  arrange(rsquare)
#> # A tibble: 142 × 6
#>   country   continent data              model  model_glance      rsquare
#>   <fct>     <fct>     <list>            <list> <list>              <dbl>
#> 1 Rwanda    Africa    <tibble [12 × 4]> <lm>   <tibble [1 × 12]>  0.0172
#> 2 Botswana  Africa    <tibble [12 × 4]> <lm>   <tibble [1 × 12]>  0.0340
#> 3 Zimbabwe  Africa    <tibble [12 × 4]> <lm>   <tibble [1 × 12]>  0.0562
#> 4 Zambia    Africa    <tibble [12 × 4]> <lm>   <tibble [1 × 12]>  0.0598
#> 5 Swaziland Africa    <tibble [12 × 4]> <lm>   <tibble [1 × 12]>  0.0682
#> 6 Lesotho   Africa    <tibble [12 × 4]> <lm>   <tibble [1 × 12]>  0.0849
#> # ℹ 136 more rows

13.0.3 회귀모형 시각화

데이터셋 by_country를 이용하여 각 나라별로 회귀모형 \(R^2\) (결정 계수) 값을 기반으로 “적합국”과 “비적합국”을 분류하고, 그 결과를 시각화한다. \(R^2\) 값이 큰 나라 5개와 작은 나라 5개를 추출하여 기대수명 변화를 그래프로 시각화하면 국가별 차이를 명확히 보여준다.

최대 \(R^2\) 값의 국가 추출:
- by_country 데이터셋에서 rsquare 값이 가장 큰 5개의 국가를 추출한다.
- 해당 국가 이름들을 rsquare_max_countries에 저장한다.
최소 \(R^2\) 값의 국가 추출:
- by_country 데이터셋에서 rsquare 값이 가장 작은 5개의 국가를 추출한다.
- 해당 국가 이름들을 rsquare_min_countries에 저장한다.
데이터 필터링 및 시각화:
- 총 10개 국가에 해당하는 데이터만 by_country에서 추출한다.
- 추출된 데이터에서 나라명, 대륙명, \(R^2\) 값, 그리고 원데이터를 추출한다.
- 결과를 \(R^2\) 값의 내림차순으로 정렬한다.
- 데이터를 정리하여 각 나라의 연도별 기대수명을 나타내는 선그래프를 생성하고, 그래프에서는 \(R^2\) 값이 높은 국가들을 “발전된국가”로, 낮은 값을 가진 국가들을 “개발국”으로 분류하여 색상을 달리하여 시각화할 재료로 준비한다.

rsquare_max_countries <- by_country |> 
  slice_max(order_by = rsquare, n = 5)  |> 
  pull(country) |> 
  droplevels()

rsquare_min_countries <- by_country |> 
  slice_min(order_by = rsquare, n = 5) |> 
  pull(country) |> 
  droplevels()

by_country |> 
  filter(country %in% c(rsquare_max_countries, rsquare_min_countries)) |> 
  select(country, continent, rsquare, data) |> 
  arrange(desc(rsquare)) |> 
  unnest(data) |> 
  mutate(country = factor(country, levels = c(rsquare_max_countries, rsquare_min_countries))) |> 
  mutate(class = if_else(country %in% rsquare_max_countries, "선진국", "개발국")) |> 
  ggplot(aes(x = year, y = lifeExp, color = class)) +
    geom_line() +
    facet_wrap(~country, nrow = 2) +
    scale_color_manual(values = c("red", "blue")) +
    theme_minimal() +
    theme(legend.position = "none",
          axis.text.x = element_text(angle = 90, vjust = 0.5, hjust=1)) +
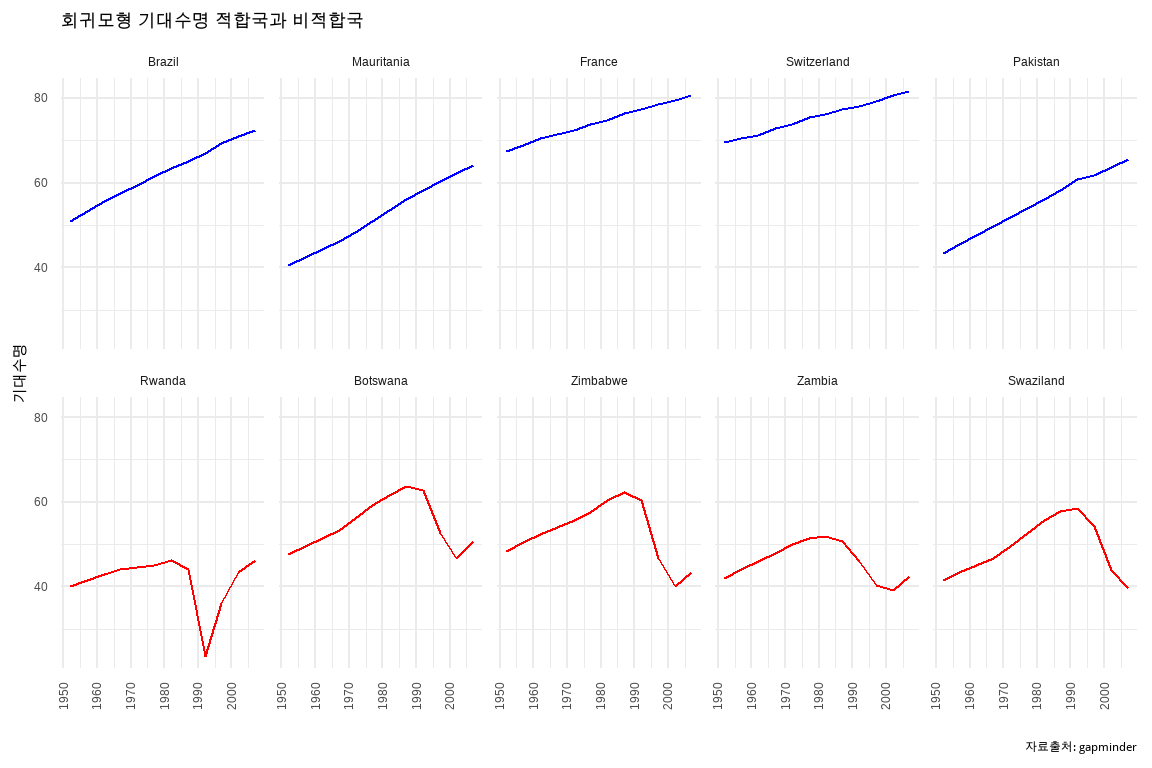
    labs(title ="회귀모형 기대수명 적합국과 비적합국",
         x = "",
         y = "기대수명",
         caption = "자료출처: gapminder")

최종적으로는 각 국가별로 연도에 따른 기대수명 변화를 보여주는 그래프를 생성한다. \(R^2\) 값이 높은 국가들은 빨간색으로, 낮은 국가들은 파란색으로 표시하고, 마지막으로 회귀모형이 얼마나 잘 적합되었는지에 따라 각 국가의 기대수명 변화 패턴을 비교한다. 파란색으로 회귀모형이 잘 적합된 경우에도 서로 다른 패턴이 확인된다. 즉, 선진국과 개발도상국 모두 제2차 세계대전 이후 기대수명이 증대했으나 선진국은 높은 기대수명에서, 개도국은 낮은 기대수명에서 시작해서 모두 기대수명이 높아진 것이 눈에 띈다. 하지만, 빨간색으로 회귀계수가 낮은 나라는 기대수명이 높아지다가 특정 사건으로 인해 기대수명이 제자리로 돌아온 이후 다시 기대수명이 높아지는 추세를 보여 비선형적 관계를 보여주고 있어 회귀계수가 전반적으로 낮게 나타났다.

13.1 모형식별

회귀모형에서 모형 식별(model identification)은 적합한 회귀모형을 선택하는 과정으로 데이터에 가장 잘 맞는 변수들을 선택하고, 모형의 형태를 결정하는 매우 중요한 과정이다. 모형 식별은 주로 변수 선택, 모형 선형성, 오차의 독립성 및 등분산성, 변수 간의 다중공선성 문제 등을 종합적으로 고려하여 진행된다. 적절한 모형을 식별하는 작업은 예측 정확도를 높이고, 데이터에 내재된 본질적인 관계를 더 잘 이해하는 데 도움이 된다.

purrr 패키지를 활용하여 원본 모형 데이터와 모형을 하나의 데이터프레임(tibble)에 리스트 칼럼으로 담을 수 있다. 즉, 6가지 서로 다른 회귀모형을 일괄적으로 적합시키고 가장 AIC 값이 적은 회귀모형을 선택하는 코드(Ovando 2018)를 다음과 같이 작성하여 many models 기법을 응용하여 모형식별에 적용할 수 있다.

reg_models: 다양한 회귀모형을 정의한다.
mutate(map()): 정의한 회귀모형 각각을 적합시키고 모형성능 지표를 추출한다.
AIC 기준으로 가장 낮은 모형을 선정한다.

library(tidyverse)
library(gapminder)

## 데이터셋 준비 -----
gapminder <- gapminder %>%
  set_names(colnames(.) %>% tolower())

## 다양한 회귀모형 -----
reg_models <- list(
  `01_pop` = 'lifeexp ~ pop',
  `02_gdppercap` = 'lifeexp ~ gdppercap',
  `03_simple` = 'lifeexp ~ pop + gdppercap',
  `04_medium` = 'lifeexp ~ pop + gdppercap + continent + year',
  `05_more`   = 'lifeexp ~ pop + gdppercap + country + year',
  `06_full`   = 'lifeexp ~ pop + gdppercap + year*country')

model_tbl <- tibble(reg_formula = reg_models) %>%
  mutate(model_name = names(reg_formula)) %>% 
  select(model_name, reg_formula) %>% 
  mutate(reg_formula = map(reg_formula, as.formula))

model_tbl
#> # A tibble: 6 × 2
#>   model_name   reg_formula 
#>   <chr>        <named list>
#> 1 01_pop       <formula>   
#> 2 02_gdppercap <formula>   
#> 3 03_simple    <formula>   
#> 4 04_medium    <formula>   
#> 5 05_more      <formula>   
#> 6 06_full      <formula>

## 회귀모형 적합 및 모형 성능 지표 -----
model_tbl <- model_tbl %>%
  mutate(fit = map(reg_formula, ~lm(., data = gapminder))) %>% 
  mutate(model_glance = map(fit, broom::glance),
         rsquare      = map_dbl(model_glance, ~.$r.squared),
         AIC          = map_dbl(model_glance, ~.$AIC)) %>% 
  arrange(AIC)

model_tbl
#> # A tibble: 6 × 6
#>   model_name   reg_formula  fit          model_glance      rsquare    AIC
#>   <chr>        <named list> <named list> <named list>        <dbl>  <dbl>
#> 1 06_full      <formula>    <lm>         <tibble [1 × 12]> 0.976    7752.
#> 2 05_more      <formula>    <lm>         <tibble [1 × 12]> 0.932    9268.
#> 3 04_medium    <formula>    <lm>         <tibble [1 × 12]> 0.717   11420.
#> 4 03_simple    <formula>    <lm>         <tibble [1 × 12]> 0.347   12836.
#> 5 02_gdppercap <formula>    <lm>         <tibble [1 × 12]> 0.341   12850.
#> 6 01_pop       <formula>    <lm>         <tibble [1 × 12]> 0.00422 13553.

회귀모형의 성능을 평가하는 데 사용된 지표들을 살펴보면, 모형 간의 비교에서 결정계수(\(R^2\))와 AIC 값이 중요하다. \(R^2\)는 모형이 데이터를 얼마나 잘 설명하는지를 나타내며, AIC는 모형의 적합도와 복잡성 사이의 균형을 평가하는 대표적인 지표로 낮은 AIC 값을 가진 모형이 일반적으로 선호된다.

모형식별 결과 ‘06_full’ 모델이 가장 낮은 AIC 값을 가지고 있으며, 높은 \(R^2\) 값을 나타내고 있어, ‘06_full’ 모형이 데이터에 가장 적합하며, 다른 모형들보다 더 정확하고 일반화할 수 있는 모형으로 채택된다.

13.2 교차검증 `CV`

과거에는 컴퓨팅 자원이 부족하여 데이터에 회귀모형을 적합시키는 것이 어려운 일이었으나, 현재는 상황이 달라져 데이터 과학자, 즉 인적 자원의 가치가 높아졌다. 중요한 작업에서는 단순히 하나의 회귀모형을 적용하는 것이 아니라, 데이터를 여러 부분으로 나누고 교차검증을 통해 가장 낮은 RMSE 값을 가진 모형을 선정함으로써 위험도를 줄이고 신뢰성을 높일 수 있다. cross_df() 함수를 사용하여 교차검증을 위한 데이터와 모형을 준비하고, analysis() 함수로 각 회귀모형을 적합시킨 뒤, assessment() 함수를 통해 모형의 성능을 평가한다. 마지막으로 RMSE 지표를 기준으로 최적의 모형을 선택한다.

## 교차검정 -----
valid_tbl <- gapminder %>%
  rsample::vfold_cv(10)

cv_tbl <- list(test_training = list(valid_tbl), 
               model_name = model_tbl$model_name)  
  
cv_tbl <- tidyr::expand_grid(test_training = list(valid_tbl), 
                             model_name = model_tbl$model_name)

cv_tbl <- cv_tbl %>%
  mutate(model_number = row_number()) %>%  
  left_join(model_tbl %>% select(model_name, reg_formula), by = "model_name") %>% 
  unnest(cols = c(test_training))

cv_tbl
#> # A tibble: 60 × 5
#>   splits             id     model_name model_number reg_formula 
#>   <list>             <chr>  <chr>             <int> <named list>
#> 1 <split [1533/171]> Fold01 06_full               1 <formula>   
#> 2 <split [1533/171]> Fold02 06_full               1 <formula>   
#> 3 <split [1533/171]> Fold03 06_full               1 <formula>   
#> 4 <split [1533/171]> Fold04 06_full               1 <formula>   
#> 5 <split [1534/170]> Fold05 06_full               1 <formula>   
#> 6 <split [1534/170]> Fold06 06_full               1 <formula>   
#> # ℹ 54 more rows

## 교차검정 analysis, assessment -----
cv_fit_tbl <- cv_tbl %>%
  mutate(fit = map2(reg_formula, splits, ~lm(.x, data = rsample::analysis(.y)))) %>%
  mutate(RMSE = map2_dbl(fit, splits, ~modelr::rmse(.x, rsample::assessment(.y))))

cv_fit_tbl
#> # A tibble: 60 × 7
#>   splits             id     model_name model_number reg_formula  fit     RMSE
#>   <list>             <chr>  <chr>             <int> <named list> <name> <dbl>
#> 1 <split [1533/171]> Fold01 06_full               1 <formula>    <lm>    2.71
#> 2 <split [1533/171]> Fold02 06_full               1 <formula>    <lm>    2.32
#> 3 <split [1533/171]> Fold03 06_full               1 <formula>    <lm>    2.60
#> 4 <split [1533/171]> Fold04 06_full               1 <formula>    <lm>    2.58
#> 5 <split [1534/170]> Fold05 06_full               1 <formula>    <lm>    2.63
#> 6 <split [1534/170]> Fold06 06_full               1 <formula>    <lm>    2.31
#> # ℹ 54 more rows

## 시각화 -----
cv_fit_tbl %>%
  ggplot(aes(RMSE, fill = model_name)) +
    geom_density(alpha = 0.75) +
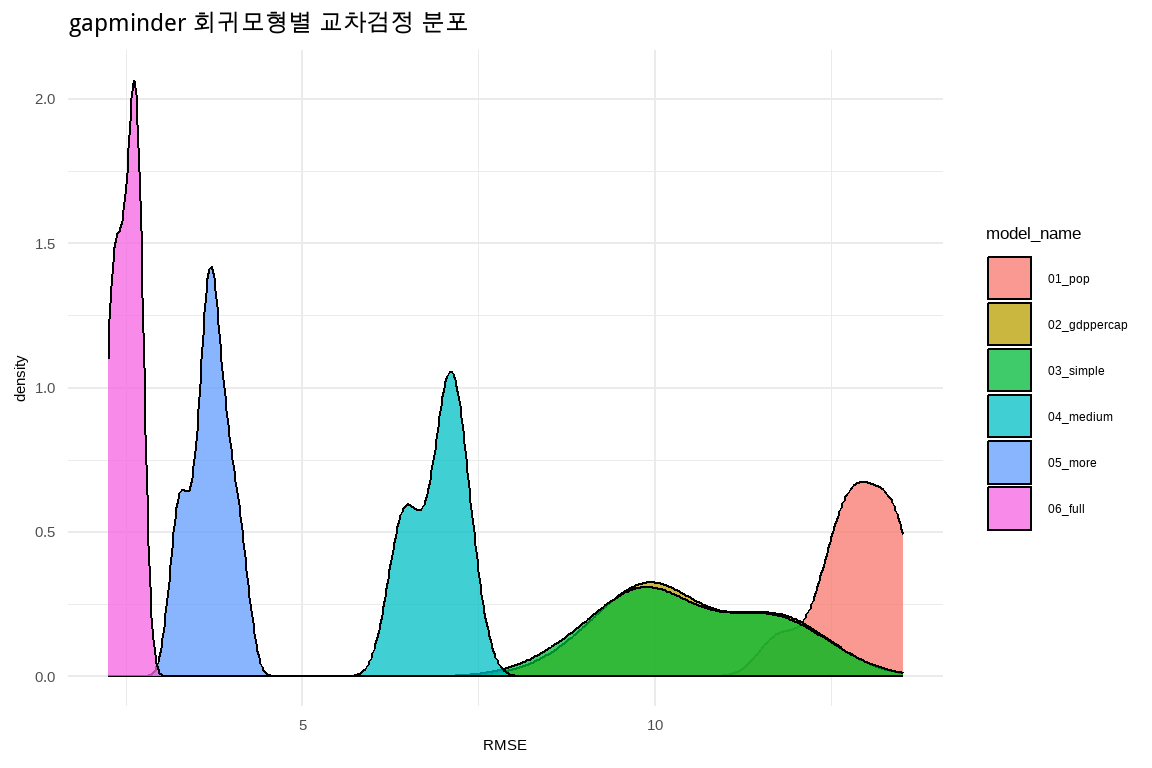
    labs(x = "RMSE", title = "gapminder 회귀모형별 교차검정 분포")

그림 13.2를 통해 교차검증 RMSE 시각화 결과를 해석하면, 모형 ‘06_full’이 일관적으로 낮은 RMSE 값을 가지고 있어 가장 성능이 우수한 것으로 보인다. 다른 모형에 비해 ’06_full’ 모형의 RMSE 분포가 좁고 낮게 유지되고 있어 일관적이고 정확한 예측 능력을 의미하고 있다. 반면, ‘03_simple’, ‘02_gdppercap’, ‘01_pop’ 같은 모형들은 상대적으로 높은 RMSE 값을 보여주고 있어, 예측 정확도가 더 낮은 것으로 해석된다. 따라서 ‘06_full’ 모형을 최적 회귀모형으로 선택해도 무방하다.

13.3 병렬처리 - `furrr`

furrr 패키지를 사용하는 주된 이유는 purrr의 기능을 확장하여 병렬 처리를 가능하게 하기 위함이다. purrr는 강력한 함수형 프로그래밍 기능을 제공하지만, 기본적으로 순차적으로 작업을 처리한다. 반면, furrr는 future 패키지와 결합되어 purrr의 함수형 패턴을 유지하면서도 작업을 여러 코어 또는 컴퓨터에 분산시켜 실행할 수 있게 해준다. 이를 통해 데이터 처리 및 모형 개발 작업에서 처리 시간을 크게 단축할 수 있다. 특히, furrr는 대용량 데이터를 다룰 때나 복잡한 통계모형, 기계학습 모형과 같은 계산 집약적인 작업에 유용하게 사용될 수 있다.

앞서 작성한 교차검증 코드를 furrr 패키지를 활용하여 병렬처리하는 방법을 살펴보자. 먼저, parallel::detectCores() 함수를 사용하여 전체 코어 수를 파악하고, future 패키지를 활용하여 교차검증 과정을 병렬 처리함으로써 처리 시간을 상당히 줄일 수 있다. 시간 절약 효과를 측정하기 위해 tictoc 패키지가 사용된다. 이 방법은 효율적인 자원 활용을 통해 데이터 처리 과정을 최적화한다.

library(furrr)
library(tictoc)

plan(multisession, workers = parallel::detectCores() - 1)

purrr 순차처리

## purrr 순차처리 -----
tic()

cv_fit_tbl <- cv_tbl %>%
  mutate(fit = map2(reg_formula, splits, ~lm(.x, data = rsample::analysis(.y))))

toc()
#> 1.25 sec elapsed

furrr 병렬처리

## furrr 병렬처리 ----
tic()

cv_fit_tbl <- cv_tbl %>%
  mutate(fit = future_map2(reg_formula, splits, ~lm(.x, data = rsample::analysis(.y)), .progress=TRUE)) 

toc()
#> 19.74 sec elapsed

병렬처리가 순차처리보다 더 많은 시간이 걸리는 현상은 여러 요인에 의해 발생할 수 있다. 병렬처리는 작업을 여러 프로세스로 분할하고 관리하는 데 추가적인 시간이 필요하기 때문에 각 작업의 실행 시간이 빨라지더라도 전체적인 성능이 반드시 항상 향상되는 것은 아니다. 병렬처리는 자원(메모리, CPU) 사용량 증가로 전체 시스템에 추가적인 부담을 준다. 특히 작은 규모의 작업에 병렬처리를 적용할 때 이런 현상이 더욱 두드러진다.

13.4 요약

데이터 과학에서 사용되는 다양한 기법들, 특히 많은 회귀모형(many models) 기법과 모형 식별, 교차검증, 병렬처리 등을 중점적으로 다루고 있다. Many models 기법은 복잡한 데이터셋 내에서 각 세부 요소에 단순한 모형을 독립적으로 적용함으로써 전체 데이터의 이해도를 높이고 숨겨진 패턴을 발견하는 데 유용하다. gapminder 데이터셋의 국가별 기대수명 데이터에 적용하여 회귀모형을 구축하고 시각화하는 과정을 보여준다.

또한 purrr 패키지를 활용하여 다양한 회귀모형을 일괄적으로 적합시키고 AIC 기준으로 최적 모형을 선택하는 모형 식별 과정을 설명한다. 이어서 교차검증을 통해 모형의 성능을 평가하고 RMSE 지표를 기준으로 최적의 모형을 선택하는 방법도 소개하고 있다. 마지막으로 furrr 패키지를 사용하여 교차검증 과정을 병렬처리함으로써 처리 시간을 단축하는 방법을 제시한다.