18  함수형 프로그래밍

함수형 프로그래밍(Wickham 2019)은 데이터 과학에서 중추적인 역할을 한다. 특정 연산을 수행하는 함수에 집중하며, 참조 투명성을 통해 동일한 입력에 대해 일관된 출력을 보장함으로써 데이터 분석 예측 가능성과 재현성을 강화한다. 또한, 데이터 분석 과정을 단순화하고 디버깅 및 테스팅을 용이하게 하는 동시에 부수 효과를 최소화한다. R 언어에서는 purrr 패키지(Wickham, Çetinkaya-Rundel, 와/과 Grolemund 2023)를 통해 함수형 프로그래밍을 구현하고 있다.

함수형 프로그래밍(functional programming)은 코드를 작성하는 한 방식으로 특정 연산을 수행하는 함수를 먼저 작성하고 나서, 사용자가 함수를 호출해서 작업을 수행하는 방식이다. 순수 함수형 언어, 예를 들어 하스켈(Haskell)은 루프가 없다. 루프 없이 어떻게 프로그램을 작성할 수 있을까? 루프는 재귀(recursion)로 대체된다. 이런 이유로 아래에서 뉴턴 방법을 통해 근을 구하는 방식을 R코드로 두 가지 방법을 보여준다. R은 아직 꼬리 호출(tail-call recurssion) 기능을 제공하지 않기 때문에 루프를 사용하는 것이 더 낫다.

수학 함수는 멋진 특성이 있는데, 즉 해당 입력에 항상 동일한 결과를 갖는다. 이 특성을 참조 투명성(referential transparaency) 이라고 부른다. 참조 투명성은 부수효과(side effect) 없음을 표현하는 속성인데, 함수가 결과값 외에 다른 상태를 변경시킬 때 부수효과(side effect)가 있다고 한다. 부수 효과는 프로그램 버그를 발생시키는 온상으로, 부수 효과를 없애면 디버깅이 용이해진다. 따라서, 부수 효과를 제거하고 참조 투명성을 유지함으로써 데이터 분석 수행 결과를 예측 가능한 상태로 유지시켜 재현가능한 과학이 가능하게 된다.

함수형 프로그래밍

R 함수형 프로그래밍을 이해하기 위해서는 먼저 자료구조에 대한 이해가 선행되어야 한다. 그리고 나서, 함수를 작성하는 이유와 더불어 작성법에 대한 이해도 확고히 해야만 한다.

객체(object)가 함수를 갖는 데이터라면, 클로저는 데이터를 갖는 함수다.

“An object is data with functions. A closure is a function with data.” – John D. Cook

명령형 언어(Imperative Language) 방식으로 R코드를 쭉 작성하게 되면, 각 단계별로 상태가 변경되는 것에 대해 신경을 쓰고 관리를 해나가야 한다. 그렇지 않으면 예기치 않은 부수 효과가 발생하여 데이터 분석 및 모형을 잘못 해석하게 된다.

그렇다고, 부수효과가 없는 순수 함수가 반드시 좋은 것은 아니다. 예를 들어 rnorm() 함수를 통해 평균 0, 분산 1인 난수를 생성시키는데, 항상 동일한 값만 뽑아내면 사용자에게 의미 있는 함수는 아니다.

결국, 함수형 프로그래밍을 통해 테스팅(testing)과 디버깅(debugging)을 수월하게 하는 것이 추구하는 바이다. 이를 위해 다음 3가지 요인이 중요하다.

18.1 왜 함수형 프로그래밍인가?

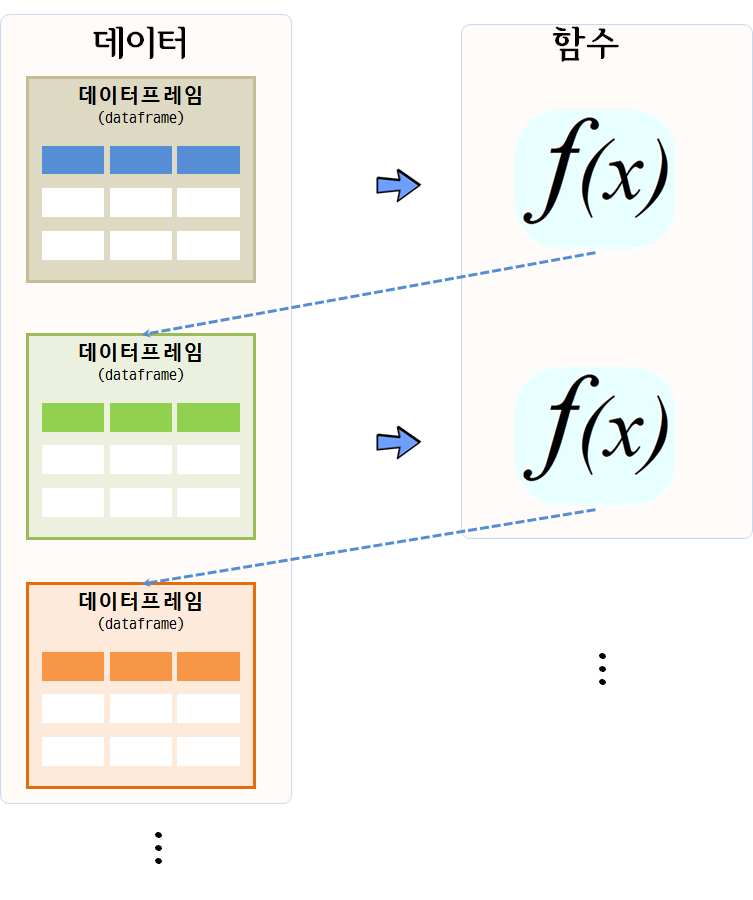
데이터 분석을 아주 추상화해서 간략하게 얘기한다면 데이터프레임을 함수에 넣어 새로운 데이터프레임을 만들어내는 과정이다.

데이터 분석, 데이터 전처리, 변수 선택, 모형 개발이 한 번에 해결되는 것이 아니라서, 데이터프레임을 함수에 넣어 상태가 변경된 데이터프레임이 생성되고, 이를 다시 함수에 넣어 또 다른 변경된 상태 데이터프레임을 얻게 되는 과정을 쭉 반복해나간다.

함수로 이해하는 데이터 분석

데이터 분석 작업흐름
그림 18.1: 데이터프레임과 함수형 프로그래밍

데이터 분석 작업에는 함수형 프로그래밍 패러다임을 활용하는 것이 좋다. 함수형 프로그래밍은 함수를 일급 객체로 취급하며, 함수 입력과 출력에 초점을 맞추고 있다. 데이터 분석의 중요한 특성인 데이터 변환, 필터링, 집계 등을 간결하고 명확하게 표현할 수 있는 장점이 크다. 함수형 프로그래밍에서는 불변성(immutability)을 강조하여 데이터 변경을 최소화하고, 함수 간의 의존성을 줄여 코드 안정성과 재현성을 높이는 데 도움이 된다.

반면에 툴이나 패키지 개발에는 객체지향 프로그래밍(OOP) 패러다임을 사용하는 것이 권장된다. 객체지향 프로그래밍은 데이터와 해당 데이터를 다루는 메서드(함수)를 하나의 객체로 묶어 관리함으로써 코드의 모듈화, 캡슐화, 재사용성을 높이는 데 도움이 된다. 객체지향 프로그래밍에서는 클래스를 정의하고, 클래스 간의 상속과 다형성을 활용하여 코드의 구조를 체계화할 수 있어 패키지 개발에서 중요한 특성인 코드의 유지보수성, 확장성, 협업 용이성 등을 향상시킬 수 있다.

데이터 분석과 툴/패키지 도구 개발

데이터 분석과 툴/패키지 도구 개발

18.2 뉴튼 방법

뉴튼 방법은 데이터 과학에서 최적화 문제를 해결하는 데 강력한 도구로 사용된다. 머신러닝과 딥러닝에서는 여러 알고리즘의 기반이 되며, 모형 파라미터를 효율적으로 업데이트하고 최적화하는 데 활용되고, 통계 분석에서 최대 가능도 추정, 일반화 선형 모델 등의 모형 파라미터를 추정하고 최적화하는 데 뉴튼 방법을 심심치 않게 보게 된다.

뉴튼-랩슨 알고리즘으로도 알려진 뉴튼(Newton Method) 방법은 컴퓨터를 사용해서 수치해석 방법으로 실함수의 근을 찾아내는 방법부터 차근차근 들어가보자.

특정 함수 \(f\) 의 근을 찾을 경우, 함수 미분값 \(f'\), 초기값 \(x_0\)가 주어지면 근사적 근에 가까운 값은 다음과 같이 정의된다.

\[x_{1} = x_0 - \frac{f(x_0)}{f'(x_0)}\]

이 과정을 반복하게 되면 오차가 매우 적은 근의 값에 도달하게 된다.

\[x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)}\]

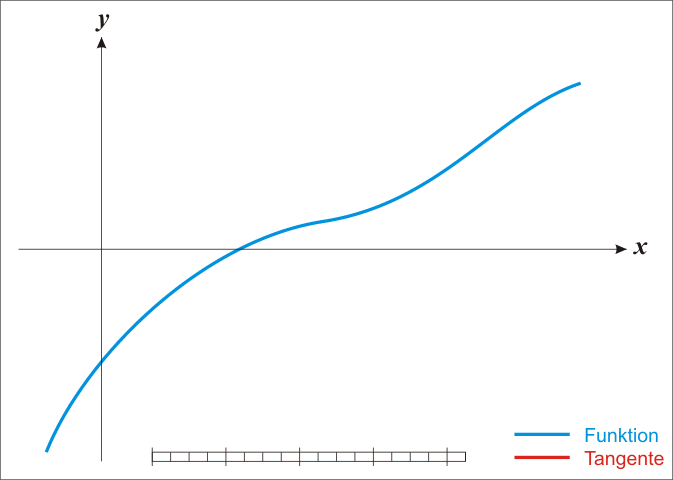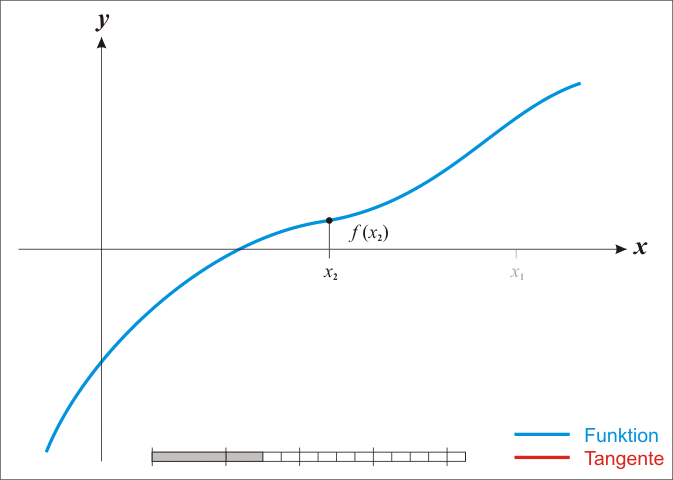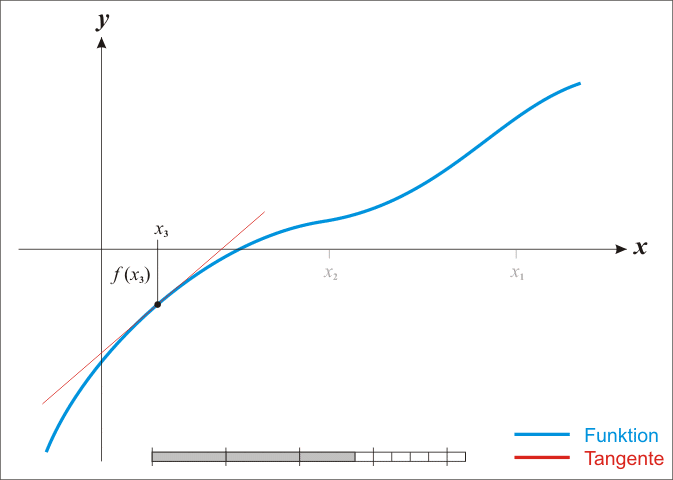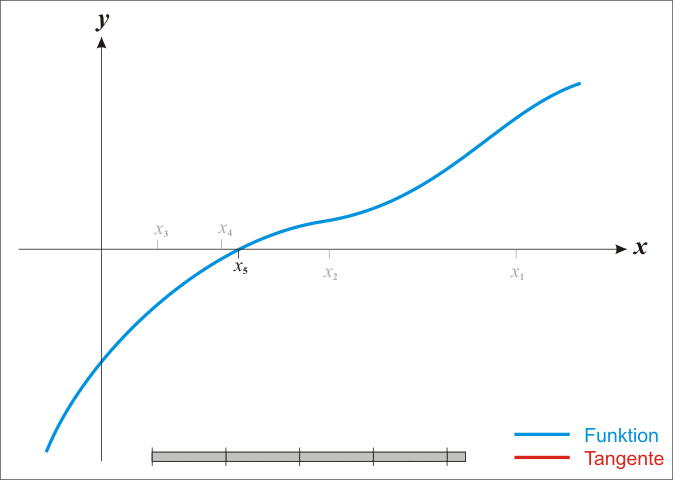
기하적으로 보면, 파란 선은 함수 \(f\) 이고, \(f\)를 미분한 \(f'\) 빨간 선은 뉴턴방법을 활용하여 근을 구해가는 과정을 시각적으로 보여주고 있다. \(x_{n-1}\) 보다 \(x_n\)이, \(x_n\) 보다 \(x_{n+1}\)이 함수 \(f\) 근에 더 가깝게 접근해 나가는 것이 확인된다.

그림 18.2: 뉴튼 방법 도식화(출처: 위키백과)

18.3 뉴튼 방법 R 코드

뉴튼 방법을 R코드로 구현하면 다음과 같이 612의 제곱근 값을 수치적으로 컴퓨터를 활용(Rodrigues 2016)하여 구할 수 있다. while같은 루프를 활용하여 반복적으로 해를 구하는 것도 가능하지만 재귀를 활용하여 해를 구하는 방법이 코드를 작성하고 읽는 개발자 관점에서는 훨씬 더 편리하고 권장된다. 하지만, 속도는 while 루프를 사용하는 것이 R에서는 이득이 많다. 이유는 오랜 세월에 걸쳐 최적화 과정을 거쳐 진화했기 때문이다.

find_root <- function(guess, init, eps = 10^(-10)){
    while(abs(init**2 - guess) > eps){
        init <- 1/2 *(init + guess/init)
        cat("현재 값: ", init, "\n")
    }
    return(init)
}

find_root(612, 10)
#> 현재 값:  35.6 
#> 현재 값:  26.39551 
#> 현재 값:  24.79064 
#> 현재 값:  24.73869 
#> 현재 값:  24.73863 
#> 현재 값:  24.73863
#> [1] 24.73863
find_root_recur <- function(guess, init, eps = 10^(-10)){
    if(abs(init**2 - guess) < eps){
        return(init)
    } else{
        init <- 1/2 *(init + guess/init)
        cat("재귀방법 현재 값: ", init, "\n")
        return(find_root_recur(guess, init, eps))
    }
}

find_root_recur(612, 10)
#> 재귀방법 현재 값:  35.6 
#> 재귀방법 현재 값:  26.39551 
#> 재귀방법 현재 값:  24.79064 
#> 재귀방법 현재 값:  24.73869 
#> 재귀방법 현재 값:  24.73863 
#> 재귀방법 현재 값:  24.73863
#> [1] 24.73863

18.4 Map, Reduce, *apply 함수

Map(), Reduce(), *apply() 계열 함수들은 R에서 함수형 프로그래밍을 구현하는 데 핵심적인 도구다. 벡터, 리스트, 행렬 등 자료구조에 대해 함수를 적용하고 그 결과를 반환하는 기능을 제공한다. for 루프를 명시적으로 사용하지 않고도 데이터에 대한 반복 연산을 수행할 수 있게 해주므로, 코드의 가독성과 효율성을 높이는 데 도움이 된다.

함수를 인자로 받는 함수를 고차함수(Higher-order function)라고 부른다. 대표적인 고차함수로 Map()과 Reduce()가 있다. 숫자 하나가 아닌 벡터에 대한 제곱근을 구하기 위해 Map() 함수를 사용하는 사례부터 살펴보고, Map(), Reduce(), *apply() 계열 함수들의 기본 개념과 사용 방법에 대해 살펴본다. 1 2

18.4.1 Map() 함수

Map() 함수를 사용하여 벡터의 각 요소에 대해 find_root_recur() 함수를 적용하는 방법은 Map() 함수가 주어진 함수를 벡터 각 요소에 적용한다. 벡터의 각 요소에 대해 개별적으로 함수를 호출하므로, 벡터의 길이가 길어질수록 함수 호출 횟수가 증가했다. 코드의 가독성 측면에서는 Map() 함수를 사용하여 벡터에 함수를 적용하는 것이 명확하게 표현된다.

반면에 find_vec_root_recur() 함수를 정의하여 캡슐화하여 벡터 전체에 대해 한 번에 제곱근을 계산하는 방법은 find_vec_root_recur() 함수가 벡터를 인자로 받아 벡터 전체에 대해 find_root_recur() 함수를 적용한다. Map() 함수를 find_vec_root_recur() 함수 내부에서 사용하여 벡터 각 요소에 대해 find_root_recur() 함수를 적용했다. 벡터 전체에 대해 한 번의 함수 호출로 제곱근을 계산하므로, 함수 호출 횟수는 벡터의 길이와 관계없이 일정하다. 코드의 가독성 측면에서는 find_vec_root_recur() 함수를 별도로 정의하여 사용하므로, 벡터에 대한 제곱근 계산 로직이 함수 내부에 캡슐화되어 있다.

성능 측면에서 보면, 후자 find_vec_root_recur() 함수를 사용하는 것이 더 효율적일 수 있다. 벡터 전체에 대해 한 번의 함수 호출로 제곱근을 계산하므로, 함수 호출 오버헤드가 줄어들 수 있기 때문이다. 하지만, 가독성 측면에서 첫 번째 방법이 Map() 함수를 직접 사용하여 벡터에 함수를 적용하는 것이 명확하게 드러나는 반면, 두 번째 방법은 벡터에 대한 제곱근 계산 로직을 별도 함수로 캡슐화하여 코드의 구조를 더 깔끔하게 만들 수 있다는 면에서 호불호가 갈린다.

# 제곱근 함수 -------------------------------------------

find_root_recur <- function(guess, init, eps = 10^(-10)){
    if(abs(init**2 - guess) < eps){
        return(init)
    } else{
        init <- 1/2 *(init + guess/init)
        return(find_root_recur(guess, init, eps))
    }
}

# 벡터에 대한 제곱근 계산 
numbers <- c(16, 25, 36, 49, 64, 81)
Map(find_root_recur, numbers, init=1, eps = 10^-10)
#> [[1]]
#> [1] 4
#> 
#> [[2]]
#> [1] 5
#> 
#> [[3]]
#> [1] 6
#> 
#> [[4]]
#> [1] 7
#> 
#> [[5]]
#> [1] 8
#> 
#> [[6]]
#> [1] 9
# `Map` 벡터 제곱근 계산

find_vec_root_recur <- function(numbers, init, eps = 10^(-10)){
    return(Map(find_root_recur, numbers, init, eps))
}

numbers_z <- c(9, 16, 25, 49, 121)
find_vec_root_recur(numbers_z, init=1, eps=10^(-10))
#> [[1]]
#> [1] 3
#> 
#> [[2]]
#> [1] 4
#> 
#> [[3]]
#> [1] 5
#> 
#> [[4]]
#> [1] 7
#> 
#> [[5]]
#> [1] 11

18.4.2 lapply 함수

lapply()와 sapply()를 사용한 방법은 Map()을 사용한 방법과 유사하게 모두 벡터 각 요소에 대해 함수를 적용하는 기능제공을 목표로 개발되었다. purrr 패키지가 도입되기 이전 R 코드에서 흔히 사용되는 함수다.

lapply()는 벡터 각 요소에 대해 함수를 적용하고 그 결과를 리스트로 반환한다. 따라서 lapply(numbers_z, find_root_recur, init=1, eps=10^(-10))은 numbers_z 벡터의 각 요소에 대해 find_root_recur() 함수를 적용하고, 그 결과를 리스트로 반환하는 반면, sapply()는 결과를 가능한 경우 벡터나 행렬로 단순화하여 반환한다는 면에서 차이가 난다.

앞선 Map() 함수를 사용한 방법과 비교하면, lapply()와 sapply()는 추가 인자를 전달하는 방식에서 차이가 있다. Map()에서는 Map(find_root_recur, numbers, init=1, eps=10^-10)과 같이 함수의 인자를 순서대로 나열하는 반면, lapply()와 sapply()에서는 lapply(numbers_z, find_root_recur, init=1, eps=10^(-10))와 같이 함수와 추가 인자 순서를 바꿔 전달한다.

# `lapply` 활용 제급근 계산
lapply(numbers_z, find_root_recur, init=1, eps=10^(-10))
#> [[1]]
#> [1] 3
#> 
#> [[2]]
#> [1] 4
#> 
#> [[3]]
#> [1] 5
#> 
#> [[4]]
#> [1] 7
#> 
#> [[5]]
#> [1] 11
sapply(numbers_z, find_root_recur, init=1, eps=10^(-10))
#> [1]  3  4  5  7 11

18.4.3 Reduce 함수

Reduce 함수도 삶을 편안하게 할 수 있는, 루프를 회피하는 또 다른 방법이다. 이름에서 알 수 있듯이 numbers_z 벡터 원소 각각에 대해 해당 연산작업 +, %%을 수행시킨다. %%는 나머지 연산자로 기본 디폴트 설정으로 \(\frac{10}{7}\)로 몫 대신에 나머지 3을 우선 계산하고, 그 다음으로 \(\frac{3}{5}\)로 최종 나머지 3을 순차적으로 계산하여 결과를 도출한다.

# Reduce ----------------------------------------------
numbers_z
#> [1]   9  16  25  49 121
Reduce(`+`, numbers_z)
#> [1] 220

numbers_z <- c(10,7,5)
Reduce(`%%`, numbers_z)
#> [1] 3

Reduce() 함수를 사용하여 뉴턴-랩슨 방법으로 제곱근을 구하는 알고리즘을 벡터에 적용하는 코드를 작성했다. newton_sqrt() 함수는 뉴턴-랩슨 방법을 사용하여 주어진 숫자의 제곱근을 구하는 함수이다. Reduce() 함수의 첫 번째 인자로는 누적 결과와 현재 요소를 받아 새로운 누적 결과를 반환하는 함수를 전달하고, 두 번째 인자는 입력 벡터, init 인자로는 초기 누적 결과를 지정한다. Reduce() 함수는 벡터의 각 요소에 대해 newton_sqrt() 함수를 호출하고, 그 결과를 누적 결과 벡터에 추가하여 최종적으로 벡터의 각 요소에 대한 제곱근 값을 계산한다.

# 뉴턴-랩슨 방법으로 제곱근 구하는 함수
newton_sqrt <- function(x, x0, eps = 1e-10) {
  x1 <- x0 - (x0^2 - x) / (2 * x0)
  if (abs(x1 - x0) < eps) {
    return(x1)
  } else {
    return(newton_sqrt(x, x1, eps))
  }
}

# 숫자 벡터
numbers <- c(16, 25, 36, 49, 64, 81)

# Reduce를 사용하여 벡터의 각 요소에 대해 제곱근 계산
sqrt_values <- Reduce(function(acc, x) c(acc, newton_sqrt(x, 1)), numbers, 
                      init = numeric())

# 결과 출력
print(sqrt_values)
#> [1] 4 5 6 7 8 9

18.5 purrr 팩키지

*apply 계열 함수는 각각의 자료형에 맞춰 사용해야 하므로 기억하기가 쉽지 않아, 매번 도움말을 찾아 확인하고 코딩을 해야 하는 번거로움이 있다. 이러한 불편함을 해소하고 데이터 분석을 함수형 프로그래밍 패러다임으로 실행할 수 있도록 purrr 패키지가 개발되었다. purrr 패키지는 함수형 프로그래밍 도구를 제공하여 데이터 분석 작업을 보다 수월하게 만들어준다. 이를 통해 데이터 분석 작업의 효율성이 향상되고, 코드의 가독성과 유지보수성도 높아질 것으로 기대된다. purrr 패키지를 활용하면 데이터 분석에 더욱 집중할 수 있게 되어, 저녁이 있는 삶을 영위할 수 있는 시간이 늘어날 것이다.

purrr 팩키지를 불러와서 map_dbl() 함수에 구문에 맞게 작성하면 동일한 결과를 깔끔하게 얻을 수 있다. 즉,

  • map_dbl(): 벡터, 데이터프레임, 리스트에 대해 함수를 원소별로 적용시켜 결과를 double 숫자형으로 출력시킨다.
  • numbers: 함수를 각 원소별로 적용시킬 벡터 입력값
  • find_root_recur: 앞서 작성한 뉴턴 방법으로 제곱근을 수치적으로 구하는 사용자 정의함수
  • init=1, eps = 10^-10: 뉴턴 방법을 구현한 사용자 정의함수에 필요한 초기값
library(purrr)
numbers <- c(16, 25, 36, 49, 64, 81)
map_dbl(numbers, find_root_recur, init=1, eps = 10^-10)
#> [1] 4 5 6 7 8 9
존 챔버스(John Chambers) 창시자가 말하는 R 계산 기본원칙
  • 존재하는 모든 것은 객체다. (Everything that exists is an object.)
  • 일어나는 모든 것은 함수호출이다. (Everything that happens is a function call.)
class(`%>%`)
#> [1] "function"
class(`$`)
#> [1] "function"
class(`<-`)
#> [1] "function"
class(`+`)
#> [1] "function"

18.6 순수한 함수 vs 불순한 함수

순수한 함수(pure function)는 입력값에만 출력값이 의존하게 되는 특성과 부수효과(side-effect)를 갖지 않는 반면 순수하지 않은 함수(impure function)는 환경에 의존하며 부수효과도 갖는다.

순수한 함수(pure function)

min(1:100)
#> [1] 1

mean(1:100)
#> [1] 50.5

순수하지 않은 함수(impure function)

Sys.time()
#> [1] "2024-04-09 00:27:14 KST"

rnorm(10)
#>  [1]  0.3663996  0.9929719  0.8315134  1.7259261  0.6756868  0.4725037
#>  [7]  0.9844674  2.2644526 -2.6676527 -0.0531321

# write_csv("data/sample.csv")

18.6.1 무명함수와 매퍼

\(\lambda\) (람다), 무명(anonymous) 함수는 함수명을 갖는 일반적인 함수와 비교하여 함수의 좋은 점은 그대로 누리면서 함수가 많아 함수명으로 메모리가 난잡하게 지저분해지는 것도 막을 수 있다.

무명함수로 기능을 구현한 후에 매퍼(mapper)를 사용해서 as_mapper() 명칭을 부여하여 함수처럼 사용하는 것도 가능하다. 매퍼(mapper)를 사용하는 이유는 다음과 같이 정리할 수 있다.

  • 간결함(Concise)
  • 가독성(Easy to read)
  • 재사용성(Reusable)

2016년 제19대 대통령선거에서 가장 큰 영향력을 발휘한 SNS는 단연 페이스북이다. 제19대 대선 당시 주요후보들의 페이스북에서 추출한 일자별 팬수 데이터를 분석해보자. 먼저, 정치인 페이스북 페이지에서 팬수를 불러온다. 그리고 이름을 부여한 리스트(named list)로 일자별 팬수 추이를 리스트로 준비한다. 그리고 나서 안철수, 문재인, 심상정 세 후보에 대한 최고 팬수증가를 무명함수로 계산한다.

library(tidyverse)
## 데이터프레임을 리스트로 변환
ahn_df  <- read_csv("data/fb_ahn.csv")  %>% rename(fans = ahn_fans) %>% 
  mutate(fans_lag = lag(fans),
         fans_diff = fans - fans_lag) %>% 
  select(fdate, fans = fans_diff) %>% 
  filter(!is.na(fans))

moon_df <- read_csv("data/fb_moon.csv") %>% rename(fans = moon_fans) %>% 
  mutate(fans_lag = lag(fans),
         fans_diff = fans - fans_lag) %>% 
  select(fdate, fans = fans_diff) %>% 
  filter(!is.na(fans))

sim_df  <- read_csv("data/fb_sim.csv")  %>% rename(fans = sim_fans) %>% 
  mutate(fans_lag = lag(fans),
         fans_diff = fans - fans_lag) %>% 
  select(fdate, fans = fans_diff) %>% 
  filter(!is.na(fans))

convert_to_list <- function(df) {
  df_fans_v <- df$fans %>% 
    set_names(df$fdate)
  return(df_fans_v)
}

ahn_v  <- convert_to_list(ahn_df)
moon_v <- convert_to_list(moon_df)
sim_v  <- convert_to_list(sim_df)

fans_lst <- list(ahn_fans  = ahn_v,
                 moon_fans = moon_v,
                 sim_fans  = sim_v)

## 데이터 살펴보기
fans_rows <- map(fans_lst, ~head(.x, 5))
fans_date <- map(fans_lst, ~head(names(.x), 5))

tibble("날짜" = fans_rows[[1]] %>% names(),
       "안철수"  = fans_rows[[1]] %>% as.numeric(),
       "문재인" = fans_rows[[2]] %>% as.numeric(),
       "심상정"  = fans_rows[[3]] %>% as.numeric())
#> # A tibble: 5 × 4
#>   날짜       안철수 문재인 심상정
#>   <chr>       <dbl>  <dbl>  <dbl>
#> 1 2017-01-02      4    413    167
#> 2 2017-01-03     31    397    134
#> 3 2017-01-04     33    465    145
#> 4 2017-01-05    290    381    133
#> 5 2017-01-06    140    511    144

## 무명함수 테스트
map_dbl(fans_lst, ~max(.x))
#>  ahn_fans moon_fans  sim_fans 
#>       796      1464      2029

rlang_lambda_function 무명함수로 increase_1000_fans 작성해서 일별 팬수 증가가 1000명 이상인 경우 keep() 함수를 사용해서 각 후보별로 추출할 수 있다. discard() 함수를 사용해서 반대로 버려버릴 수도 있다.

increase_1000_fans <- as_mapper( ~.x > 1000)

map(fans_lst, ~keep(.x, increase_1000_fans))
#> $ahn_fans
#> named numeric(0)
#> 
#> $moon_fans
#> 2017-03-28 2017-04-18 2017-04-20 
#>       1464       1310       1093 
#> 
#> $sim_fans
#> 2017-03-12 2017-03-13 2017-04-14 2017-04-19 2017-04-20 2017-04-21 2017-04-24 
#>       1301       1079       1070       1441       1190       1025       1948 
#> 2017-04-25 
#>       2029

술어논리(predicate logic)는 조건을 테스트하여 참(TRUE), 거짓(FALSE)을 반환시킨다. every, some을 사용하여 팬수가 증가한 날이 매일 1,000명이 증가했는지, 전부는 아니고 일부 특정한 날에 1,000명이 증가했는지 파악할 수 있다.

## 세후보 팬수가 매일 모두 1000명 이상 증가했나요?
map(fans_lst, ~every(.x, increase_1000_fans))
#> $ahn_fans
#> [1] FALSE
#> 
#> $moon_fans
#> [1] FALSE
#> 
#> $sim_fans
#> [1] FALSE
## 세후보 팬수가 전체는 아니고 일부 특정한 날에 1000명 이상 증가했나요?
map(fans_lst, ~some(.x, increase_1000_fans))
#> $ahn_fans
#> [1] FALSE
#> 
#> $moon_fans
#> [1] TRUE
#> 
#> $sim_fans
#> [1] TRUE

18.6.2 고차 함수

고차 함수(High order function)는 함수의 인자로 함수를 받아 함수로 반환시키는 함수를 지칭한다. high_order_fun 함수는 함수를 인자(func)로 받아 함수를 반환시키는 고차함수다. 평균 함수(mean)를 인자로 넣어 출력값으로 mean_na() 함수를 새롭게 생성시킨다. NA가 포함된 벡터를 넣어 평균값을 계산하게 된다.

high_order_fun <- function(func){
  function(...){
    func(..., na.rm = TRUE)
  }
}

mean_na <- high_order_fun(mean)
mean_na( c(NA, 1:10) )
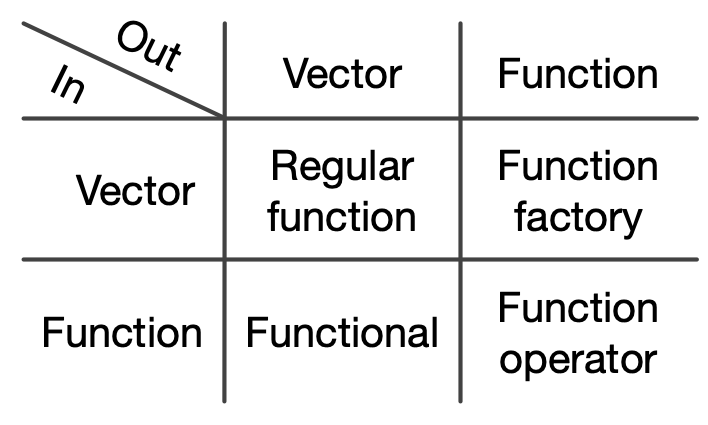
#> [1] 5.5

벡터가 입력값으로 들어가서 벡터가 출력값으로 나오는 보통 함수(Regular Function)외에 고차함수는 3가지 유형이 있다.

  • 벡터 → 벡터: 정규함수
  • 벡터 → 함수: 함수공장
  • 함수 → 벡터: Functional - for루프를 purrr 팩키지 map() 함수로 대체
  • 함수 → 함수: 함수연산자(Function Operator) - Functional과 함께 사용될 경우 adverbs로서 강력한 기능을 발휘

고차함수 유형

고차함수 유형

18.6.3 부사: safely, possibly,…

purrr 팩키지의 대표적인 부사(adverbs)에는 possibly()와 safely()가 있다. 그 외에도 silently(), surely() 등 다른 부사도 있으니 필요한 경우 purrr 팩키지 문서를 참조한다.

safely(mean)은 동사 함수(mean())를 받아 부사 safely()로 “부사 + 동사”로 기능이 추가된 부사 동사를 반환시킨다. 따라서, NA가 추가된 벡터를 넣을 경우 $result와 $error를 원소로 갖는 리스트를 반환시킨다.

mean_safe <- safely(mean)
class(mean_safe)
#> [1] "function"

mean_safe(c(NA, 1:10))
#> $result
#> [1] NA
#> 
#> $error
#> NULL

이를 활용하여 오류처리작업을 간결하게 수행시킬 수 있다. $result와 $error를 원소로 갖는 리스트를 반환시키기 때문에 오류와 결과값을 추출하여 후속작업을 수행하여 디버깅하는 데 유용하게 활용할 수 있다.

test_lst <- list("NA", 1,2,3,4,5)
log_safe <- safely(log)

map(test_lst, log_safe) %>% 
  map("result")
#> [[1]]
#> NULL
#> 
#> [[2]]
#> [1] 0
#> 
#> [[3]]
#> [1] 0.6931472
#> 
#> [[4]]
#> [1] 1.098612
#> 
#> [[5]]
#> [1] 1.386294
#> 
#> [[6]]
#> [1] 1.609438

map(test_lst, log_safe) %>% 
  map("error")
#> [[1]]
#> <simpleError in .Primitive("log")(x, base): 수학함수에 숫자가 아닌 인자가 전달되었습니다>
#> 
#> [[2]]
#> NULL
#> 
#> [[3]]
#> NULL
#> 
#> [[4]]
#> NULL
#> 
#> [[5]]
#> NULL
#> 
#> [[6]]
#> NULL

반면에 possibly()는 결과와 otherwise 값을 반환시켜서 오류가 발생되면 중단되는 것이 아니라 오류가 있다는 사실을 알고 예외처리시킨 후에 쭉 정상진행시킨다.

max_possibly <- possibly(sum, otherwise = "watch out")

max_possibly(c(1:10))
#> [1] 55

max_possibly(c(NA, 1:10))
#> [1] NA

max_possibly(c("NA", 1:10))
#> [1] "watch out"

possibly()는 부울 논리값, NA, 문자열, 숫자를 반환시킬 수 있다. transpose()와 결합하여 safely(), possibly() 결과를 변형시킬 수도 있다.

map(test_lst, log_safe) %>% length()
#> [1] 6

map(test_lst, log_safe) %>% transpose() %>% length()
#> [1] 2

compact()를 사용해서 NULL을 제거하는데, 앞서 possibly()의 인자로 otherwise=를 지정하는 경우 otherwise=NULL와 같이 정의해서 예외처리로 NULL을 만들어내고 compact()로 정상처리된 데이터만 얻는 작업흐름을 갖춘다.

null_lst <- list(1, NULL, 3, 4, NULL, 6, 7, NA)
compact(null_lst)
#> [[1]]
#> [1] 1
#> 
#> [[2]]
#> [1] 3
#> 
#> [[3]]
#> [1] 4
#> 
#> [[4]]
#> [1] 6
#> 
#> [[5]]
#> [1] 7
#> 
#> [[6]]
#> [1] NA

possibly_log <- possibly(log, otherwise = NULL)
map(null_lst, possibly_log) %>% compact()
#> [[1]]
#> [1] 0
#> 
#> [[2]]
#> [1] 1.098612
#> 
#> [[3]]
#> [1] 1.386294
#> 
#> [[4]]
#> [1] 1.791759
#> 
#> [[5]]
#> [1] 1.94591
#> 
#> [[6]]
#> [1] NA

18.7 깨끗한 코드

round_mean() 함수를 compose() 함수를 사용해서 mean() 함수로 평균을 구한 후에 round()함수로 반올림하는 코드를 다음과 같이 쉽게 작성할 수 있다. 3

round_mean <- compose(round, mean)
round_mean(1:10)
#> [1] 6

두 번째 사례로 전형적인 데이터 분석 사례로 lm() → anova() → tidy()를 통해 한 방에 선형회귀 모형 산출물을 깨끗한 코드로 작성하는 사례를 살펴보자.

mtcars 데이터셋에서 연비 예측에 변수 두 개를 넣고 일반적인 lm() 선형예측모형 제작방식과 동일하게 인자를 넣는다.

clean_lm <- compose(broom::tidy, anova, lm)
clean_lm(mpg ~ hp + wt, data=mtcars)
#> # A tibble: 3 × 6
#>   term         df sumsq meansq statistic   p.value
#>   <chr>     <int> <dbl>  <dbl>     <dbl>     <dbl>
#> 1 hp            1  678. 678.       101.   5.99e-11
#> 2 wt            1  253. 253.        37.6  1.12e- 6
#> 3 Residuals    29  195.   6.73      NA   NA

compose()를 통해 함수를 조합하는 경우 함수의 인자를 함께 전달해야 될 경우가 있다. 이와 같은 경우 partial()을 사용해서 인자를 넘기는 함수를 제작하여 compose()에 넣어준다.

robust_round_mean <- compose(
  partial(round, digits=1),
  partial(mean, na.rm=TRUE))
robust_round_mean(c(NA, 1:10))
#> [1] 5.5

리스트 컬럼(list-column)과 결합하여 모형에서 나온 데이터 분석결과를 깔끔하게 코드로 제작해보자. 먼저 lm을 돌려 모형 요약하는 함수 summary를 통해 r.squared값을 추출하는 함수를 summary_lm으로 제작한다.

그리고 나서 nest() 함수로 리스트 컬럼(list-column)을 만들고 두 개의 집단 수동/자동을 나타내는 am 변수를 그룹으로 삼아 두 집단에 속한 수동/자동 데이터에 대한 선형 회귀모형을 적합시키고 나서 “r.squared”값을 추출하여 이를 티블 데이터프레임에 저장시킨다.

summary_lm <- compose(summary, lm) 

mtcars %>%
  group_by(am) %>%
  nest() %>%
  mutate(lm_mod = map(data, ~ summary_lm(mpg ~ hp + wt, data = .x)),
         r_squared = map(lm_mod, "r.squared")) %>%
  unnest(r_squared)
#> # A tibble: 2 × 4
#> # Groups:   am [2]
#>      am data               lm_mod     r_squared
#>   <dbl> <list>             <list>         <dbl>
#> 1     1 <tibble [13 × 10]> <smmry.lm>     0.837
#> 2     0 <tibble [19 × 10]> <smmry.lm>     0.768

18.8 사례: 붓꽃 데이터셋

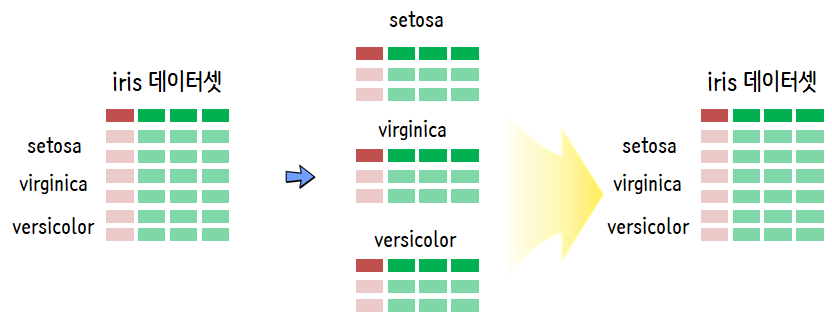
구글 검색을 통해서 쉽게 iris(붓꽃) 데이터를 구할 수 있다. 이를 불러와서 각 종별로 setosa versicolor, virginica로 나눠 로컬 .csv 파일로 저장하고 나서 이를 다시 불러오는 사례를 함수형 프로그래밍으로 구현해본다.

그림 18.3: 붓꽃 데이터 불러오기

먼저 iris.csv 파일을 R로 불러와서 각 종별로 나눠서 iris_종명.csv 파일 형식으로 저장시킨다.

library(tidyverse)
iris_df <- read_csv("https://gist.githubusercontent.com/curran/a08a1080b88344b0c8a7/raw/d546eaee765268bf2f487608c537c05e22e4b221/iris.csv")

iris_species <- iris_df %>% 
  count(species) %>% pull(species)

for(i in 1:length(iris_species)) {
  tmp_df <- iris_df %>% 
    filter(species == iris_species[i])
  tmp_df %>% write_csv(paste0("data/iris_", iris_species[i], ".csv"))
}

Sys.glob("data/iris_*.csv")
#> [1] "data/iris_setosa.csv"     "data/iris_versicolor.csv"
#> [3] "data/iris_virginica.csv"

로컬 파일 iris_종명.csv 형식으로 저장된 데이터를 함수형 프로그래밍을 통해 불러와서 분석 작업을 수행해 보자. map() 함수를 사용하여 각 종별로 데이터를 깔끔하게 불러왔다. 먼저, iris_species 벡터에 붓꽃 종의 이름을 추출하여 저장하고, 이를 활용하여 iris_종명.csv과 경로명이 포함된 문자열을 생성하였다.

그다음, read_csv() 함수를 map() 함수를 통해 iris_species 벡터의 각 원소에 적용하여 데이터를 읽어들였다. 이렇게 읽어들인 데이터는 리스트 형태로 iris_list 객체에 저장되었다. 이제 iris_list에는 각 붓꽃 종별로 데이터가 깔끔하게 정리되어 있어, 추후 분석 작업을 수월하게 진행할 수 있게 되었다.

iris_filename <- c("data/iris_setosa.csv", "data/iris_versicolor.csv", "data/iris_virginica.csv")

iris_list <- map(iris_filename, read_csv) %>% 
  set_names(iris_species)

iris_list |> enframe()
#> # A tibble: 3 × 2
#>   name       value              
#>   <chr>      <list>             
#> 1 setosa     <spc_tbl_ [50 × 5]>
#> 2 versicolor <spc_tbl_ [50 × 5]>
#> 3 virginica  <spc_tbl_ [50 × 5]>

iris_list 각 원소는 데이터프레임이라 summary 함수를 사용해서 기술 통계량을 구할 수도 있다. 물론 cor() 함수를 사용해서 iris_list의 각 원소를 지정하는 .x 여기서는 종별 데이터프레임에서 변수 두 개를 추출하여 sepal_length, sepal_width 이 둘 간의 스피어만 상관계수를 계산하는데 출력값이 double 연속형이라 map_dbl로 지정하여 작업시킨다.

map(iris_list, summary)
#> $setosa
#>   sepal_length    sepal_width     petal_length    petal_width   
#>  Min.   :4.300   Min.   :2.300   Min.   :1.000   Min.   :0.100  
#>  1st Qu.:4.800   1st Qu.:3.125   1st Qu.:1.400   1st Qu.:0.200  
#>  Median :5.000   Median :3.400   Median :1.500   Median :0.200  
#>  Mean   :5.006   Mean   :3.418   Mean   :1.464   Mean   :0.244  
#>  3rd Qu.:5.200   3rd Qu.:3.675   3rd Qu.:1.575   3rd Qu.:0.300  
#>  Max.   :5.800   Max.   :4.400   Max.   :1.900   Max.   :0.600  
#>    species         
#>  Length:50         
#>  Class :character  
#>  Mode  :character  
#>                    
#>                    
#>                    
#> 
#> $versicolor
#>   sepal_length    sepal_width     petal_length   petal_width   
#>  Min.   :4.900   Min.   :2.000   Min.   :3.00   Min.   :1.000  
#>  1st Qu.:5.600   1st Qu.:2.525   1st Qu.:4.00   1st Qu.:1.200  
#>  Median :5.900   Median :2.800   Median :4.35   Median :1.300  
#>  Mean   :5.936   Mean   :2.770   Mean   :4.26   Mean   :1.326  
#>  3rd Qu.:6.300   3rd Qu.:3.000   3rd Qu.:4.60   3rd Qu.:1.500  
#>  Max.   :7.000   Max.   :3.400   Max.   :5.10   Max.   :1.800  
#>    species         
#>  Length:50         
#>  Class :character  
#>  Mode  :character  
#>                    
#>                    
#>                    
#> 
#> $virginica
#>   sepal_length    sepal_width     petal_length    petal_width   
#>  Min.   :4.900   Min.   :2.200   Min.   :4.500   Min.   :1.400  
#>  1st Qu.:6.225   1st Qu.:2.800   1st Qu.:5.100   1st Qu.:1.800  
#>  Median :6.500   Median :3.000   Median :5.550   Median :2.000  
#>  Mean   :6.588   Mean   :2.974   Mean   :5.552   Mean   :2.026  
#>  3rd Qu.:6.900   3rd Qu.:3.175   3rd Qu.:5.875   3rd Qu.:2.300  
#>  Max.   :7.900   Max.   :3.800   Max.   :6.900   Max.   :2.500  
#>    species         
#>  Length:50         
#>  Class :character  
#>  Mode  :character  
#>                    
#>                    
#> 

map_dbl(iris_list, ~cor(.x$sepal_length, .x$sepal_width, method = "spearman"))
#>     setosa versicolor  virginica 
#>  0.7686085  0.5176060  0.4265165

18.9 사례: 표본추출

서로 다른 난수를 생성시키는 방법을 살펴보자. 정규분포를 가정하고 평균과 표준편차를 달리하는 모수를 지정하고 난수갯수도 숫자를 달리하여 난수를 생성시킨다.

18.9.1 \(\mu\) 평균 변화

정규분포에서 난수를 10개 추출하는데 표준편차는 1로 고정시키고, 평균만 달리한다. 평균만 달리하기 때문에 map() 함수를 그대로 사용한다. 즉, 입력값으로 평균만 달리하는 리스트를 입력값으로 넣는다.

## 평균을 달리하는 경우
normal_mean <- list(1,5,10)

sim_mu_name <- paste0("mu: ", normal_mean)

sim_mu_list <- map(normal_mean, ~ data.frame(mean = .x, 
                            random_number = rnorm(mean=.x, sd=1, n=10))) %>% 
  set_names(sim_mu_name)

map_dbl(sim_mu_list, ~mean(.x$random_number))
#>    mu: 1    mu: 5   mu: 10 
#> 1.281557 5.383674 9.651964

sim_mu_list |> enframe()
#> # A tibble: 3 × 2
#>   name   value        
#>   <chr>  <list>       
#> 1 mu: 1  <df [10 × 2]>
#> 2 mu: 5  <df [10 × 2]>
#> 3 mu: 10 <df [10 × 2]>

18.9.2 \(\mu\) 평균, \(\sigma\) 표준편차

난수갯수만 고정시키고 평균과 표준편차를 달리하여 난수를 정규분포에서 추출한다. 입력값으로 평균과 표준편차 두 개가 되기 때문에 map2() 함수를 사용한다.

## 평균과 표준편차를 달리하는 경우
normal_mean <- list(1,5,10)
normal_sd   <- list(10,5,1)

sim_mu_sd_name <- paste0("mu: ", normal_mean, ",  sd: ", normal_sd)

sim_mu_sd_list <- map2(normal_mean, normal_sd, 
                        ~ data.frame(mean = .x, sd = .y,
                            random_number = rnorm(mean=.x, sd=.y, n=10))) %>% 
  set_names(sim_mu_sd_name)

map_dbl(sim_mu_sd_list, ~sd(.x$random_number))
#> mu: 1,  sd: 10  mu: 5,  sd: 5 mu: 10,  sd: 1 
#>     11.0564335      3.6743235      0.8788563

sim_mu_sd_list |> enframe()
#> # A tibble: 3 × 2
#>   name           value        
#>   <chr>          <list>       
#> 1 mu: 1,  sd: 10 <df [10 × 3]>
#> 2 mu: 5,  sd: 5  <df [10 × 3]>
#> 3 mu: 10,  sd: 1 <df [10 × 3]>

18.9.3 \(\mu\), \(\sigma\), 표본크기

\(\mu\) 평균, \(\sigma\) 표준편차, 표본크기를 모두 다르게 지정하여 난수를 추출한다. 이런 경우 pmap() 함수를 사용하고 입력 리스트가 다수라 이를 normal_list로 한 번 더 감싸서 이름이 붙은 리스트(named list) 형태로 넣어주고, 이를 function() 함수의 내부 인수로 사용한다.

## 평균, 표준편차, 표본크기를 달리하는 경우
normal_mean <- list(1,5,10)
normal_sd   <- list(10,5,1)
normal_size <- list(10,20,30)

sim_mu_sd_size_name <- paste0("mu: ", normal_mean, ",  sd: ", normal_sd,
                              "  size: ", normal_size)

normal_list <- list(normal_mean=normal_mean, normal_sd=normal_sd, normal_size=normal_size)

sim_mu_sd_size_list <- pmap(normal_list,
                            function(normal_mean, normal_sd, normal_size)
                        data.frame(mean=normal_mean, sd = normal_sd, size = normal_size,
                            random_number = rnorm(mean=normal_mean, sd=normal_sd, n=normal_size))) %>% 
  set_names(sim_mu_sd_size_name)

map_dbl(sim_mu_sd_size_list, ~length(.x$random_number))
#> mu: 1,  sd: 10  size: 10  mu: 5,  sd: 5  size: 20 mu: 10,  sd: 1  size: 30 
#>                       10                       20                       30

sim_mu_sd_size_list |> enframe()
#> # A tibble: 3 × 2
#>   name                     value        
#>   <chr>                    <list>       
#> 1 mu: 1,  sd: 10  size: 10 <df [10 × 4]>
#> 2 mu: 5,  sd: 5  size: 20  <df [20 × 4]>
#> 3 mu: 10,  sd: 1  size: 30 <df [30 × 4]>

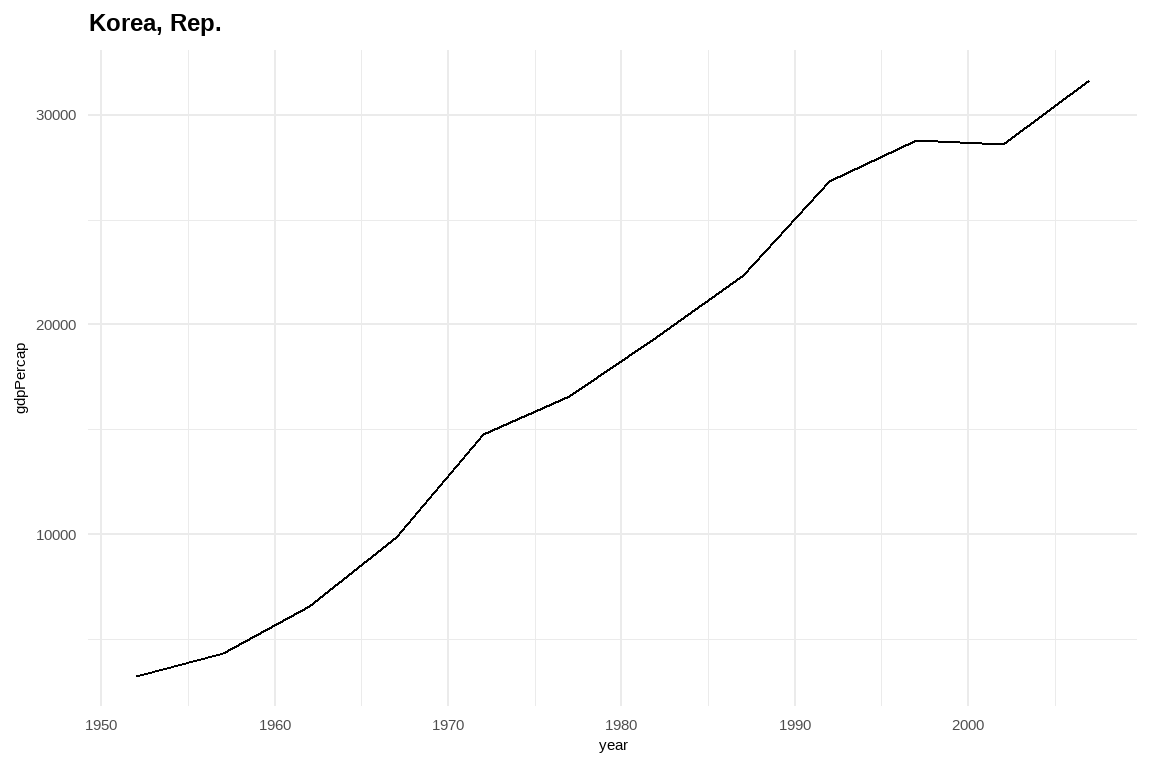
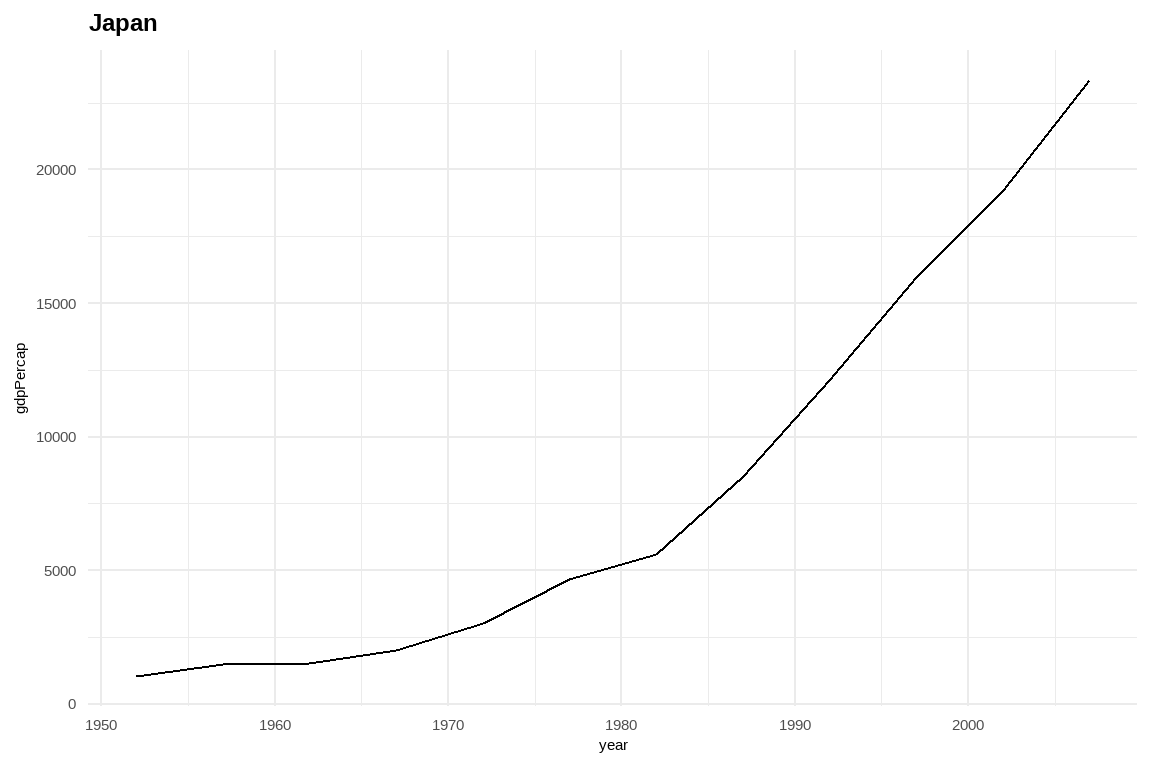
18.10 사례: ggplot 시각화

list-column을 활용하여 티블(tibble) 데이터프레임에 담아서 시각화를 진행해도 되고, 다른 방법으로 리스트에 담아서 이를 한 장에 찍는 것도 가능하다. 4

library(gapminder)

## 데이터 -----
two_country <-  c("Korea, Rep.", "Japan")

gapminder_tbl <- gapminder %>% 
  filter(str_detect(continent, "Asia")) %>% 
  group_by(continent, country) %>% 
  nest() %>% 
  select(-continent) %>% 
  filter(country %in% two_country )

## 티블 데이터 시각화 -----
gapminder_plot_tbl <- gapminder_tbl %>% 
  mutate(graph = map2(data, country, 
                     ~ggplot(.x, aes(x=year, y=gdpPercap)) +
                       geom_line() +
                       labs(title=.y)))

gapminder_plot_tbl
#> # A tibble: 2 × 4
#> # Groups:   continent, country [2]
#>   continent country     data              graph 
#>   <fct>     <fct>       <list>            <list>
#> 1 Asia      Japan       <tibble [12 × 4]> <gg>  
#> 2 Asia      Korea, Rep. <tibble [12 × 4]> <gg>

## 리스트 데이터 시각화 -----
gapminder_plot <- map2(gapminder_tbl$data , two_country, 
                     ~ggplot(.x, aes(x=year, y=gdpPercap)) +
                       geom_line() +
                       labs(title=.y))

walk(gapminder_plot, print)

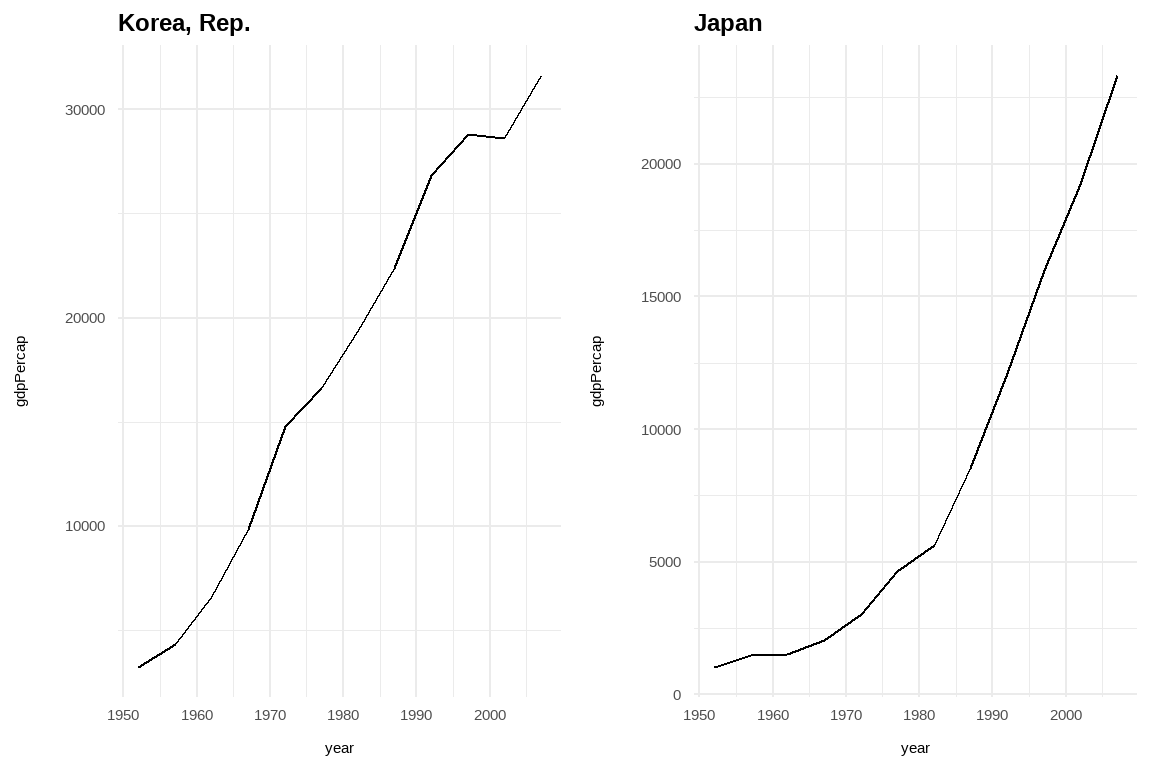
## 리스트 데이터 시각화 - 한 장에 찍기 -----
cowplot::plot_grid(plotlist = gapminder_plot)
그림 18.4: 리스트-칼럼 ggplot 시각화
그림 18.5: 리스트-칼럼 ggplot 시각화
그림 18.6: 리스트-칼럼 ggplot 시각화

18.11 요약

함수형 프로그래밍은 데이터 과학 분야에서 매우 중요한 역할을 담당한다. 특정 연산을 수행하는 함수에 초점을 맞추고, 동일한 입력에 대해 일관된 출력을 보장하는 참조 투명성을 통해 데이터 분석의 예측 가능성과 재현성을 높일 수 있다. 또한, 부수 효과를 최소화하고 테스팅과 디버깅을 용이하게 하여 데이터 분석 과정을 단순화할 수 있다.

purrr 패키지를 통해 함수형 프로그래밍을 구현할 수 있다. map, reduce, *apply 계열 함수들은 데이터에 대한 반복 연산을 수행하는 데 유용하며, 코드의 가독성과 효율성을 높여준다. 특히 purrr 패키지는 다양한 함수형 프로그래밍 도구를 제공하여 데이터 분석 작업을 보다 수월하게 만들어준다.

함수형 프로그래밍에서 순수 함수와 고차 함수의 개념이 중요하다. 순수 함수는 입력값에만 의존하고 부수 효과가 없는 함수를 의미하며, 고차 함수는 함수를 인자로 받아 함수를 반환하는 함수를 말한다. 순수 함수와 고차 함수를 통해 코드 재사용성을 높이고 레고 블록과 같이 모듈화할 수 있다.

  1. purrr tutorial: Lessons and Examples↩︎

  2. purrr tutorial GitHub Webpage↩︎

  3. Colin Fay, “A Crazy Little Thing Called {purrr} - Part 5: code optimization”↩︎

  4. Very statisticious (August 20, 2018), “Automating exploratory plots with ggplot2 and purrr”↩︎