15  함수

15.1 함수 기본 지식

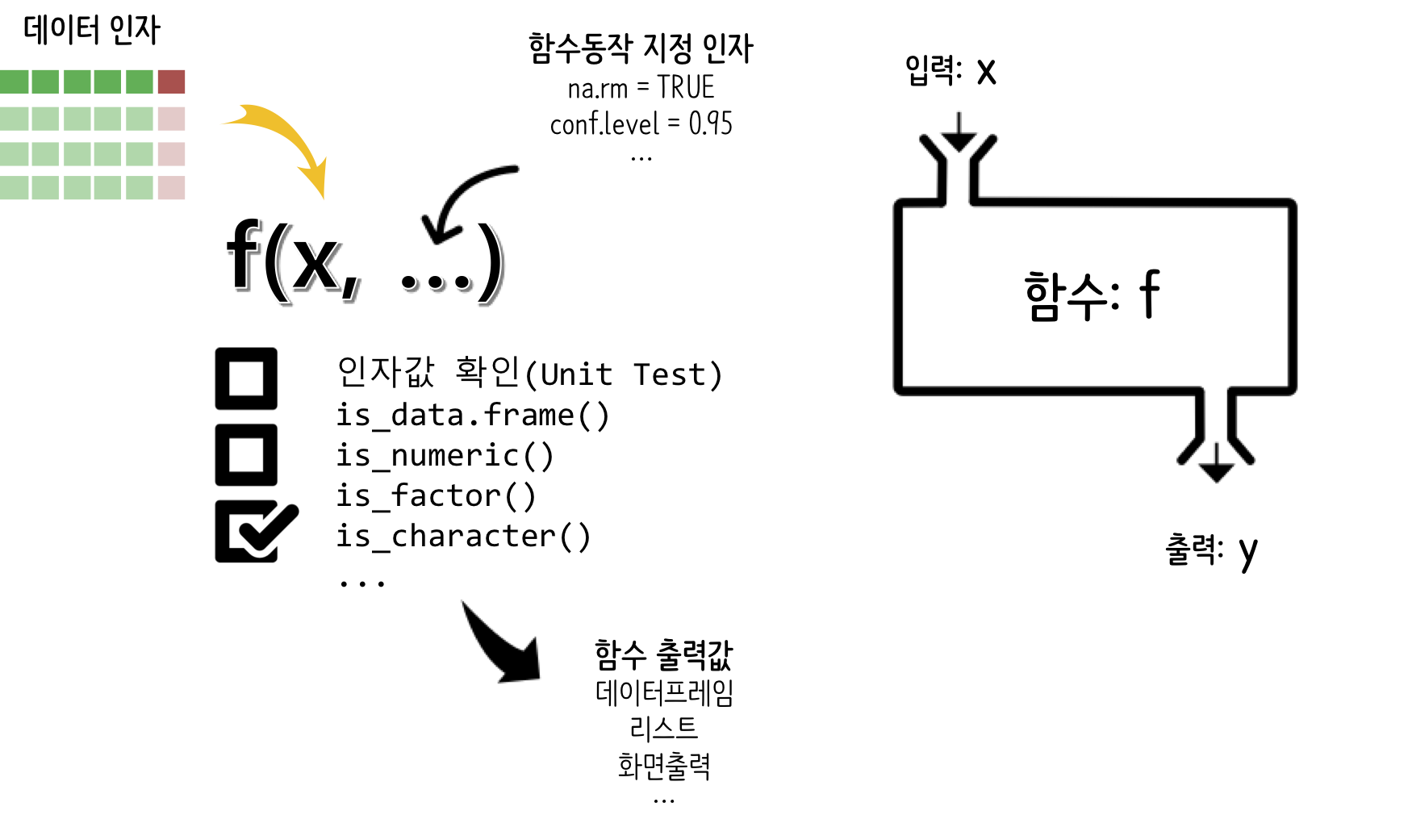
함수는 입력값(x)을 넣어 어떤 작업(f)을 수행한 결과를 반환(y)하는 과정으로 이해할 수 있는데, 인자로 다양한 값을 함수에 넣을 수 있고, 물론 함수가 유용한 작업을 수행하기 위한 전제조건을 만족시키는지 확인하는 과정을 assert 개념을 넣어 확인하고 기술된 작업을 수행한 후에 출력값을 변환시키게 된다.

그림 15.1: 데이터 과학 함수 개념

15.2 함수 사용법

본격적으로 함수를 작성하기 전에 먼저, 함수를 사용하는 방법을 익히는 것이 필요하다. 함수는 함수명, 인자(argument), 함수 몸통(body), 반환값(return value)으로 구성된다.
데이터 과학 대표 언어인 R과 파이썬으로 4칙 연산을 구현하는 함수를 작성하여 자세히 살펴보자.

15.2.1 R 함수

roxygen2는 R 패키지 개발에 널리 사용되는 문서화 도구로, 함수 코드 바로 위에 특수한 주석을 작성하여 함수의 파라미터, 반환값, 예제 등을 설명하는 방식으로 함수를 문서화하여 가독성도 높이고 오류 가능성도 줄여 재사용성에 도움이 된다.

  • 함수명: 함수명을 먼저 적고 <-, function(), {, } 순으로 R이 함수임을 알 수 있도록 전개한다.
  • 함수 인자: 함수에 넣을 인자를 정의하여 넣어둔다.
  • 함수 몸통(body): 앞서 사칙연산처럼 함수가 수행해야 하는 작업을 기술한다.
  • 반환값(return): return 예약어로 함수 작업 결과 반환되는 값을 명시할 수도 있고, 그냥 두면 마지막 객체가 자동으로 반환된다.
  • roxygen2 문법에 맞춰 함수 설명을 작성한다.
    • 과거 roxygen2 문법에 맞춘 함수 문서화 작업은 품이 많이 가고 고단한 작업이었지만 챗GPT를 비롯한 AI를 사용하면 쉽게 작업할 수 있다.
#' 두 숫자에 대한 기본 산술 연산 수행
#'
#' 이 함수는 두 개의 숫자 인자를 받아 두 숫자의 합, 차, 곱, 몫을 포함하는 리스트를 반환합니다.
#'
#' @param first 첫 번째 숫자를 나타내는 숫자 값.
#' @param second 두 번째 숫자를 나타내는 숫자 값.
#'
#' @return 다음 네 가지 요소가 포함된 리스트:
#' \itemize{
#'   \item sum_number: `first`와 `second`의 합.
#'   \item minus_number: `first`에서 `second`를 뺀 값.
#'   \item multiply_number: `first`와 `second`의 곱.
#'   \item divide_number: `first`를 `second`로 나눈 몫.
#' }
#'
#' @examples
#' basic_operation(10, 5)
#' # [[1]]
#' # [1] 15
#' #
#' # [[2]]
#' # [1] 5
#' #
#' # [[3]]
#' # [1] 50
#' #
#' # [[4]]
#' # [1] 2
#'
#' @export
basic_operation <- function(first, second) {
 sum_number <- first + second
 minus_number <- first - second
 multiply_number <- first * second
 divide_number <- first / second
 result <- list(sum_number, minus_number, multiply_number, divide_number)
 return(result)
}

basic_operation(7, 3)
#> [[1]]
#> [1] 10
#> 
#> [[2]]
#> [1] 4
#> 
#> [[3]]
#> [1] 21
#> 
#> [[4]]
#> [1] 2.333333

15.2.2 파이썬 함수

파이썬 함수는 함수명, 인자(argument), 함수 몸통(body), 반환값(return value)으로 구성된다. R 함수와 개념적으로 동일하지만 문법만 다르고 함수 설명은 docstring으로 작성된다. 물론 AI를 사용해서 함수 설명도 작성할 수 있다.

  • 함수 머리(header): def로 함수임을 선언하고, 함수명과 함수 인자를 기술한 후 마지막을 :으로 마무리한다.
  • 함수 설명: docstring으로 ““” … ““” 안에 함수에 대한 도움말을 기술한다. 함수가 하는 역할, 매개변수, 반환되는 값, 예제 등을 넣어 개발자가 봤을 때 피로도가 없도록 작성한다.
  • 함수 몸통(body): 앞서 사칙연산처럼 함수가 수행해야 하는 작업을 기술한다.
  • 반환값(return): return 예약어로 함수 작업 결과 반환되는 값을 지정한다.
def basic_operation(first, second):
    """
    숫자 두 개를 받아 사칙연산을 수행하는 함수.
    
    예제
        basic_operation(10, 20)
    매개변수(args)
        first(int): 정수형 숫자
        second(int): 정수형 숫자
    반환값(return)
        리스트: +-*/ 사칙연산 결과
    """
    sum_number = first + second
    minus_number = first - second
    multiply_number = first * second
    divide_number = first / second
    
    result = [sum_number, minus_number, multiply_number, divide_number]
    
    return result
    
basic_operation(7, 3)    
#> [10, 4, 21, 2.3333333333333335]

15.2.3 함수 호출

다른 사람이 작성한 함수를 사용한다는 것은 좀 더 엄밀한 의미로 함수를 호출(call)한다고 한다. 함수를 호출해서 다른 사람이 작성한 함수를 사용하기 위해서는 먼저 함수명을 알아야 하고, 그다음으로 함수에서 사용되는 인자(argument)를 파악해서 올바르게 전달해야 원하는 결과를 얻을 수 있다.

표준편차(sd)를 계산하는 sd 함수의 경우 전달되는 인자는 두 개로 x, na.rm = FALSE인데 이를 확인할 수 있는 명령어가 args() 함수다.

args(sd)
#> function (x, na.rm = FALSE) 
#> NULL

x는 ? sd 명령어를 통해서 숫자 벡터를 전달해 주어야만 표준편차를 계산할 수 있다. 예를 들어, 데이터프레임(penguins)의 변수 하나(bill_length_mm)를 지정하여 전달하고 na.rm = TRUE도 명세하여 인자로 전달한다. 인자값이 기본 디폴트 값으로 설정된 경우 타이핑을 줄일 수 있고, 결측값이 포함된 경우에 따라서 다른 인자를 넣어 전달하는 방식으로 함수를 사용한다.

library(palmerpenguins)
sd(penguins$bill_length_mm, na.rm = TRUE)
#> [1] 5.459584

15.3 함수 작성 시점

기본적으로 함수를 작성하는 이유는 반복적인 작업을 줄이기 위해서이다. 스크립트에 작성된 데이터 분석 코드는 다른 제3자가 작성한 함수를 사용하는 과정이다. 하지만, 제3자가 작성한 함수가 본인이 풀고 있는 문제에 맞지 않는 경우가 있다. 데이터를 다루면서 뭔가 불편하게 느껴지기 시작하면 함수 작성을 고려할 시점으로, 누구나 자연스럽게 마주하는 일상적인 경험이다.

왜 함수가 필요한지를 데이터를 분석할 때 자주 나오는 변수 정규화 사례를 바탕으로 살펴보자.1 데이터프레임에 담긴 변수의 측도가 상이하여 변수를 상대적으로 비교하기 위해 측도를 재조정하여 표준화할 필요가 있다. 변수에서 평균을 빼고 표준편차로 나누는 정규화도 있지만, 최대값에서 최소값을 빼서 분모에 두고 분자에 최소값을 빼서 나누면 모든 변수가 0–1 사이 값으로 척도가 조정된다.

\[ f(x)_{\text{척도조정}} = \frac{x-min(x)}{max(x)-min(x)} \]

df <- data.frame(a=c(1,2,3,4,5),
                         b=c(10,20,30,40,50),
                         c=c(7,8,6,1,3),
                         d=c(5,4,6,5,2))
df$a <- (df$a - min(df$a, na.rm = TRUE)) /
        (max(df$a, na.rm = TRUE) - min(df$a, na.rm = TRUE))
df$b <- (df$b - min(df$b, na.rm = TRUE)) /
        (max(df$a, na.rm = TRUE) - min(df$b, na.rm = TRUE))
df$c <- (df$c - min(df$c, na.rm = TRUE)) /
        (max(df$c, na.rm = TRUE) - min(df$c, na.rm = TRUE))
df$d <- (df$d - min(df$d, na.rm = TRUE)) /
        (max(df$d, na.rm = TRUE) - min(df$d, na.rm = TRUE))
df        
#>      a         b         c    d
#> 1 0.00  0.000000 0.8571429 0.75
#> 2 0.25 -1.111111 1.0000000 0.50
#> 3 0.50 -2.222222 0.7142857 1.00
#> 4 0.75 -3.333333 0.0000000 0.75
#> 5 1.00 -4.444444 0.2857143 0.00

상기 R 코드는 측도를 모두 맞춰서 변수 4개(a, b, c, d)를 비교하거나 향후 분석을 위한 것이다. 하지만, 읽어야 하는 코드 중복이 심하고 길어 코드를 작성한 개발자의 의도 가 본의 아니게 숨겨져 있다. 작성한 R 코드에 실수한 것이 있는 경우, 다음 프로그램 실행에서 버그(특히, 구문론이 아닌 의미론적 버그)가 숨겨지게 된다. 상기 코드가 작성되는 과정을 살펴보면 본의 아니게 의도가 숨겨진다는 의미가 어떤 것인지 명확해진다.

  1. df$a <- (df$a - min(df$a, na.rm = TRUE)) / (max(df$a, na.rm = TRUE) - min(df$a, na.rm = TRUE)) 코드를 작성한 후, 정상적으로 작동하는지 확인한다.
  2. 1번 코드가 잘 동작하게 되면 복사하여 붙여넣기 기능을 사용하여 다른 칼럼 작업을 확장해 나간다. df$b, df$c, df$d를 생성하게 된다.
  3. 즉, 복사해서 붙여넣은 것을 변수명을 편집해서 df$b, df$c, df$d 변수를 순차적으로 생성해낸다.

중복을 제거하는 한 방법이 함수를 작성하는 것이고, 함수를 작성하게 되면 의도가 명확해진다. 함수명을 rescale로 붙이고 이를 실행하게 되면, 의도가 명확하게 드러나게 되고, 복사해서 붙여넣기로 생겨나는 중복과 반복에 의한 실수를 줄일 수 있게 되며, 향후 코드를 갱신할 때도 도움이 된다.

rescale <- function(x){
  rng <- range(x, na.rm = TRUE)
  (x - rng[1]) / (rng[2] - rng[1])
}

df$a <- rescale(df$a)
df$b <- rescale(df$b)
df$c <- rescale(df$c)
df$d <- rescale(df$d)

rescale() 함수를 사용해서 복사하여 붙여넣는 중복을 크게 줄였으나, 여전히 함수명을 반복해서 복사하여 붙여넣기를 통해 코드를 작성했다. 함수형 프로그래밍을 사용하면 함수명을 반복적으로 사용하는 것조차도 피할 수 있다.

library(purrr)
df <- map_df(df, rescale)
df
#> # A tibble: 5 × 4
#>       a     b     c     d
#>   <dbl> <dbl> <dbl> <dbl>
#> 1  0     1    0.857  0.75
#> 2  0.25  0.75 1      0.5 
#> 3  0.5   0.5  0.714  1   
#> 4  0.75  0.25 0      0.75
#> 5  1     0    0.286  0

함수를 사용하지 않고 복사하여 붙여넣기 방식으로 코드를 작성한 경우 의도하지 않은 실수가 있어 함수를 도입하여 작성한 코드와 결과가 다른 것이 존재한다. 코드를 읽어 찾아보거나 실행한 후 결과를 통해 버그를 찾아보는 것도 함수의 의미와 중요성을 파악하는 데 도움이 된다.

해들리 위캠 어록


중복은 의도를 숨기게 되고, 복사하여 붙여넣기를 두 번 했다면 함수를 작성할 시점이 되었다. (Duplication hides the intent. If you have copied-and-pasted twice, it is time to write a function.)

15.4 스크립트 → 함수

함수를 작성하는 경우는 먼저 데이터를 가져와서 정제하고 EDA 과정을 거치며 모형과 시각화 산출물을 제작하는 과정을 거친다. 그리고 나서 이런 작업이 몇 번 반복하게 되면 함수 작성을 고려하게 된다. 즉, 스크립트에서 함수로 변환하는 과정을 설명하면 다음과 같다.

  1. R 함수 템플릿을 제작한다.
    • 함수명 <- function() { }
  2. 스크립트를 함수 몸통에 복사하여 붙인다.
  3. 반복 작업되는 인자를 찾아내 이를 인자로 넣어둔다.
  4. 인자값과 연동되는 부분을 찾아 맞춰준다.
  5. 함수명을 적절한 동사를 갖춘 이름으로 작명한다.
  6. return이 불필요하기 때문에 R 언어 특성을 반영하여 필요한 경우 제거한다.

주사위를 던져 나온 숫자를 구하는 함수를 작성해보자. 먼저 주사위를 모사하여 보자. 즉, 주사위를 물리적으로 만드는 대신 주사위를 던진 것과 동일한 효과가 나타나도록 이를 구현해 본다.

  1. 주사위 던지는 스크립트

먼저 주사위 눈을 1,2,3,4,5,6 숫자 벡터로 정의하고 나서 sample() 함수로 size=1을 지정한다. 즉, 주사위 눈 6개 중 임의로 하나를 선택한다.

dice <- c(1,2,3,4,5,6)

sample(dice, size=1)
#> [1] 4
  1. 함수 템플릿

“함수명 <- function() { }”으로 구성되는 함수 템플릿을 작성한다.

draw_dice <- function() {
  
}
  1. 함수 몸통으로 복사하여 붙여넣기

함수 몸통 내부에 dice <- c(1,2,3,4,5,6)을 함수를 매번 호출할 때마다 실행시킬 필요는 없기 때문에 외부로 빼내고 실제 주사위 던지는 과정을 모사하는 코드만 복사하여 붙여넣는다.

dice <- c(1, 2, 3, 4, 5, 6)

draw_dice <- function() {
  sample(dice, size=1)
}

draw_dice()
#> [1] 1
  1. 함수명, 함수 인자 등 마무리

함수명을 draw_dice 말고 다른 더 기억하기 좋고 짧고 간결한 형태로 필요한 경우 변경시키고, 인자도 없는 것에서 횟수를 지정할 수 있도록 변경시키며, 필요한 경우 return 함수를 지정하여 반환값을 명시적으로 적어둔다.

draw_dice <- function(num_try) {
  face <- sample(dice, size=num_try)
  return(face) # 불필요함.
}

draw_dice(3)
#> [1] 2 1 3

15.5 함수 구성요소

한 걸음 더 들어가, 함수를 작성할 때는 인자의 유효성 검사, 함수 몸통에서 데이터 처리, 반환값 등 다양한 측면을 고려해야 한다. 특히 인자값 검사는 함수의 안정성과 효율성을 위해 중요하며, 그 중요성을 반영하여 다양한 도구가 소개되어 있다. 또한 반환값이 여러 개인 경우에는 적절한 방법으로 반환값을 처리해야 한다. 함수를 작성할 때는 이러한 요소들을 종합적으로 고려하여 효율적이고 안정적인 함수를 구현해야 한다.

15.5.1 인자

함수 구성요소 중 중요한 요소로 인자를 꼽을 수 있다. 인자는 크게 두 가지로 나뉜다.

  • 데이터 인자(data arguments): 대다수의 함수는 기본적으로 데이터에 대한 연산을 가정하고 있다. 따라서 데이터를 함수 인자로 지정하여 이를 함수 몸통에서 처리하고 결과를 반환시키는 것은 당연한 귀결이다.
  • 동작방식 지정 인자(detail arguments): 함수가 동작하는 방식에 대해서 세부적으로 지정할 필요가 있는데 이때 필요한 것이 동작방식 지정 인자가 된다.

예를 들어 t.test() 함수를 살펴보면 x가 데이터 인자가 되며, 기타 alternative = c("two.sided", "less", "greater"), mu = 0, paired = FALSE, var.equal = FALSE, conf.level = 0.95, ...은 함수가 구체적으로 어떻게 동작하는지 명세한 인자값이다.

? t.test

## Default S3 method:
t.test(x, y = NULL,
       alternative = c("two.sided", "less", "greater"),
       mu = 0, paired = FALSE, var.equal = FALSE,
       conf.level = 0.95, ...)

15.5.2 인자값 확인 - assert

인자값이 제대로 입력되어야 함수 몸통에서 기술한 연산 작업이 제대로 수행될 수 있다. 이를 위해서 testthat, assertive, assertr, assertthat 등 수많은 패키지가 존재한다. stopifnot(), stop() 등 Base R 함수를 사용해도 문제는 없다.

다음과 같이 입력값에 NA가 포함된 경우 벡터의 합계를 구하는 함수가 동작하지 않거나 아무 의미 없는 값을 반환하곤 한다. 그리고 앞서 인자값을 잘 제어하지 않게 되면 귀중한 컴퓨팅 자원을 낭비하기도 한다. 이를 방지하기 위해서 stopifnot() 함수로 함수 몸통을 수호하는 보호자처럼 앞서 인자값의 적절성에 대해서 검정을 먼저 수행한다. 그리고 나서 사전 유효성 검사를 통과한 인자값에 대해서만 함수 몸통에 기술된 연산 작업을 수행하고 결과값을 반환시킨다.

library(testthat)

num_vector <- c(1,2,3,4, 5)
na_vector <- c(1,2,3,NA_character_, 5)

sum_numbers <- function(vec) {
  
  stopifnot(!any(is.na(vec)))
  
  total <- 0

  for(i in 1:length(vec)) {
    total <- total + vec[i]
  }
  total
}

sum_numbers(num_vector)
#> [1] 15
sum_numbers(na_vector)
#> Error in sum_numbers(na_vector): !any(is.na(vec)) is not TRUE

상기 코드의 문제점은 stopifnot() 함수가 잘못된 입력값에 대해서 문제가 무엇이고, 어떤 행동을 취해야 하는지 친절하지 않다는 데 있다. 이를 assertive 패키지를 활용해서 극복하는 방안을 살펴보자. assertive 패키지를 설치하면 R 함수 작성에 걸림돌이 될 수 있는 거의 모든 사전 점검 작업을 수행할 수 있다는 것이 매력적이다. install.packages("assertive")를 실행하게 되면 함께 설치되는 패키지는 다음과 같다.

assertive.base, assertive.properties, assertive.types, assertive.numbers, assertive.strings, assertive.datetimes, assertive.files, assertive.sets, assertive.matrices, assertive.models, assertive.data, assertive.data.uk, assertive.data.us, assertive.reflection, assertive.code

library(assertive)

sum_numbers_assertive <- function(vec) {
  
  result <- try(assert_all_are_not_na(vec), silent = TRUE)
  
  if (inherits(result, "try-error")) {
    stop("벡터에 NA 값이 있어서 총합을 구할 수 없습니다.")
  }
  
  total <- 0

  for(i in 1:length(vec)) {
    total <- total + vec[i]
  }
  
  total
}

sum_numbers_assertive(na_vector)
#> Error in sum_numbers_assertive(na_vector): 벡터에 NA 값이 있어서 총합을 구할 수 없습니다.

15.5.3 반환값 확인

R은 파이썬과 달리 return()이 꼭 필요하지는 않다. 왜냐하면 마지막 객체가 자동으로 함수 반환값으로 정의되기 때문이다. 함수 반환값과 관련하여 몇 가지 사항을 알아두면 도움이 많이 된다.

먼저 함수에서 반환되는 값이 하나가 아닌 경우 이를 담아내는 방법을 살펴보자. list()로 감싸서 이를 반환하는 경우가 많이 사용되었지만, 최근 zeallot 패키지가 도입되어 함수 출력값을 받아내는 데 간결하고 깔끔하게 작업할 수 있게 되었다. zeallot vignette에 다양한 사례가 나와 있다.

예를 들어 단변량 회귀모형의 경우 lm() 함수로 회귀식을 적합시킨다. 그리고 나서 coef() 함수로 절편과 회귀계수를 추출할 때 %<-% 연산자를 사용하게 되면 해당 값을 벡터 객체에 할당시킬 수 있다.

library(tidyverse)
library(zeallot)

c(inter, slope) %<-% coef(lm(mpg ~ cyl, data = mtcars))

cat("절편: ", inter, "\n기울기: ", slope)
#> 절편:  37.88458 
#> 기울기:  -2.87579

iris 데이터셋을 훈련/시험 데이터셋으로 쪼갠다. 이를 위해서 일양균등분포에서 난수를 생성시켜 8:2 비율로 훈련/시험 데이터를 나눈다. 그리고 나서, %<-% 연산자로 훈련/시험 데이터로 나누어 할당하는 것도 가능하다. 각 붓꽃마다 0~1 사이 난수를 생성하여 할당한다. 그리고 난수값이 0.2 이상이면 훈련, 그렇지 않으면 시험 데이터로 구분한다.

penguins_raw <-  palmerpenguins::penguins |> drop_na()
penguin_df <- penguins_raw %>% 
  mutate(runif = runif(n())) %>% 
  mutate(train_test = ifelse(runif > 0.2, "train", "test")) 

c(test, train) %<-%  split(penguin_df, penguin_df$train_test)

cat("총 관측점: ", nrow(penguins_raw), "\n훈련: ", nrow(train), "\n시험: ", nrow(test))
#> 총 관측점:  333 
#> 훈련:  253 
#> 시험:  80

혹은, 회귀분석 결과를 list() 함수로 결합시켜 리스트로 반환시킨다. 이런 경우 결과값이 하나가 아니더라도 추후 리스트 객체를 풀어 활용하는 것이 가능하다.

get_lm_statistics <- function(df) {
  mtcars_lm <- lm(mpg ~ cyl, data=df)
  
  intercept <- coef(mtcars_lm)[1]
  beta      <- coef(mtcars_lm)[2]
  
  lm_stats <- list(intercept = intercept, 
                   beta = beta)
  
  return(lm_stats)
}

mtcars_list <- get_lm_statistics(mtcars)

mtcars_list
#> $intercept
#> (Intercept) 
#>    37.88458 
#> 
#> $beta
#>      cyl 
#> -2.87579
좋은 함수란?

척도를 일치시키는 기능을 함수로 구현했지만, 기능을 구현했다고 좋은 함수가 되지는 않는다. 좋은 함수가 되는 조건은 다음과 같다.

  1. Correct: 기능이 잘 구현되어 올바르게 동작할 것
  2. Understandable: 사람이 이해할 수 있어야 함. 즉, 함수는 컴퓨터를 위해 기능이 올바르게 구현되고, 사람도 이해할 수 있도록 작성되어야 한다.
  3. 즉, Correct + Understandable: 컴퓨터와 사람을 위해 작성될 것.

한걸음 더 들어가 구체적으로 좋은 함수는 다음과 같은 특성을 지니고 있다.

  1. 함수와 인자에 대해 유의미한 명칭을 사용한다.
    • 함수명에 적절한 동사명을 사용한다.
  2. 직관적으로 인자를 배치하고 기본 디폴트값에도 추론 가능한 값을 사용한다.
  3. 함수가 인자로 받아 반환하는 것을 명확히 한다.
  4. 함수 내부 몸통 부분에 일관된 스타일을 잘 사용한다.

좋은 함수 작성과 연계하여 깨끗한 코드(Clean code)는 다음과 같은 특성을 갖고 작성된 코드를 뜻한다.

  • 가볍고 빠르다 - Light
  • 가독성이 좋다 - Readable
  • 해석 가능하다 - Interpretable
  • 유지보수가 뛰어나다 - Maintainable

연습문제

rescale 함수

함수를 작성할 경우 먼저 매우 단순한 문제에서 출발한다. 척도를 맞추는 상기 과정을 R 함수로 만드는 과정을 통해 앞서 학습한 사례를 실습해 보자.

  1. 입력값과 출력값을 정의한다. 즉, 입력값이 c(1,2,3,4,5) 으로 들어오면 출력값은 0.00 0.25 0.50 0.75 1.00 0–1 사이 값으로 나오는 것이 확인되어야 하고, 각 원소값도 출력 벡터 원소값에 매칭이 되는지 확인한다.

  2. 기능이 구현되어 동작이 제대로 되는지 확인되는 R 코드를 작성한다.

(df$a - min(df$a, na.rm = TRUE)) / (max(df$a, na.rm = TRUE) - min(df$a, na.rm = TRUE))
  1. 확장 가능하게 임시 변수를 사용해서 위에서 구현된 코드를 다시 작성한다.
( x - min( x , na.rm = TRUE)) / (max( x , na.rm = TRUE) - min( x , na.rm = TRUE))
x <- df$a
( x - min( x , na.rm = TRUE)) / (max( x , na.rm = TRUE) - min( x , na.rm = TRUE))
  1. 함수 작성 의도를 명확히 하도록 다시 코드를 작성한다.
x <- df$a
rng <- range(x, na.rm = TRUE)
(x - rng[1]) / (rng[2] - rng[1])
  1. 최종적으로 재작성한 코드를 함수로 변환한다.
x <- df$a

rescale <- function(x){
                rng <- range(x, na.rm = TRUE)
                (x - rng[1]) / (rng[2] - rng[1])
            }

rescale(x)

요약통계 함수

데이터를 분석할 때 가장 먼저 수행하는 작업이 요약통계를 통해 데이터를 이해하는 것이다. 이미 훌륭한 요약통계 패키지와 함수가 있지만, 친숙한 개념을 함수로 다시 제작함으로써 함수에 대한 이해를 높일 수 있다.

요약통계 기능을 먼저 구현한 다음에 중복을 제거하여 요약통계 기능 함수를 제작해보자. 함수도 인자로 넣어 처리할 수 있다는 점이 처음에는 이상할 수도 있지만, 함수를 인자로 처리할 경우 코드 중복을 상당히 줄일 수 있다. \(L_1\), \(L_2\), \(L_3\) 값을 구하는 함수를 다음과 같이 작성하는 경우, 숫자 1,2,3만 차이가 날 뿐 다른 부분은 동일하기 때문에 함수 코드에 중복이 심하게 관찰된다.

  • 1단계: 중복이 심한 함수, 기능 구현에 초점을 맞춰 작성한다.
f1 <- function(x) abs(x - mean(x)) ^ 1
f2 <- function(x) abs(x - mean(x)) ^ 2
f3 <- function(x) abs(x - mean(x)) ^ 3
  • 2단계: 임시 변수로 처리할 수 있는 부분을 식별하고 적절한 인자명(power)을 부여한다.
f1 <- function(x) abs(x - mean(x)) ^ power
f2 <- function(x) abs(x - mean(x)) ^ power
f3 <- function(x) abs(x - mean(x)) ^ power
  • 3단계: 식별된 변수명을 함수 인자로 변환한다.
f1 <- function(x, power) abs(x - mean(x)) ^ power
f2 <- function(x, power) abs(x - mean(x)) ^ power
f3 <- function(x, power) abs(x - mean(x)) ^ power

여기서 요약통계 함수 인자로 “데이터”(df)와 기초통계 요약 “함수”(mean, sd 등)도 함께 넘겨 요약통계 함수를 간략하고 가독성 높게 작성할 수 있다.

먼저, 특정 변수의 중위수, 평균, 표준편차를 계산하는 함수를 작성하는 경우를 가정해보자.

  • 1단계: 각 기능을 구현하는 기능 구현에 초점을 맞춰 작성한다.
col_median <- function(df) {
    output <- numeric(length(df))
    for (i in seq_along(df)) {
      output[i] <- median(df[[i]])
    }
    output
  }

col_mean <- function(df) {
    output <- numeric(length(df))
    for (i in seq_along(df)) {
      output[i] <- mean(df[[i]])
    }
    output
  }

col_sd <- function(df) {
    output <- numeric(length(df))
    for (i in seq_along(df)) {
      output[i] <- sd(df[[i]])
    }
    output
  }
  • 2단계: median, mean, sd를 함수 인자 fun으로 함수명을 통일한다.
col_median <- function(df) {
    output <- numeric(length(df))
    for (i in seq_along(df)) {
      output[i] <- fun(df[[i]])
    }
    output
  }

col_mean <- function(df) {
    output <- numeric(length(df))
    for (i in seq_along(df)) {
      output[i] <- fun(df[[i]])
    }
    output
  }

col_sd <- function(df) {
    output <- numeric(length(df))
    for (i in seq_along(df)) {
      output[i] <- fun(df[[i]])
    }
    output
  }
  • 3단계: 함수 인자 fun을 넣어 중복을 제거한다.
col_median <- function(df, fun) {
    output <- numeric(length(df))
    for (i in seq_along(df)) {
      output[i] <- fun(df[[i]])
    }
    output
  }

col_mean <- function(df, fun) {
    output <- numeric(length(df))
    for (i in seq_along(df)) {
      output[i] <- fun(df[[i]])
    }
    output
  }

col_sd <- function(df, fun) {
    output <- numeric(length(df))
    for (i in seq_along(df)) {
      output[i] <- fun(df[[i]])
    }
    output
  }
  • 4단계: 함수를 인자로 갖는 요약통계 함수를 최종적으로 정리하고, 테스트 사례를 통해 검증한다.
col_summary <- function(df, fun) {
    output <- numeric(length(df))
    for (i in seq_along(df)) {
      output[i] <- fun(df[[i]])
    }
    output
}

col_summary(df, fun = median)
#> [1] 0.5000000 0.5000000 0.7142857 0.7500000
col_summary(df, fun = mean)
#> [1] 0.5000000 0.5000000 0.5714286 0.6000000
col_summary(df, fun = sd)
#> [1] 0.3952847 0.3952847 0.4164966 0.3791438

15.6 요약

함수는 입력값을 받아 어떤 작업을 수행한 후 결과를 반환하는 과정으로 이해할 수 있으며, 함수명, 인자, 함수 몸통, 반환값으로 구성된다. 함수는 동일한 개념이지만 구문만 차이남을 R과 파이썬으로 함수를 작성하는 방법과 문서화하는 방법을 사례로 통해 설명하고 있다.

함수를 작성하는 주된 이유는 반복적인 작업을 줄이기 위함이다. 데이터를 다루면서 불편함을 느끼기 시작하면 함수 작성을 고려하게 되는데, 이는 누구나 자연스럽게 마주하는 일상적인 경험이다. 변수 정규화 사례를 통해 함수 작성의 필요성과 중요성을 강조하고 있다.

함수 작성 시에는 인자의 유효성 검사, 함수 몸통에서의 데이터 처리, 반환값 등 다양한 측면을 고려해야 한다. 특히 인자값 검사는 함수의 안정성과 효율성을 위해 중요하며, 이를 위한 다양한 도구가 소개되어 있다. 또한 반환값이 여러 개인 경우에는 적절한 방법으로 반환값을 처리해야 한다.

마지막으로 연습문제를 통해 척도 조정 함수인 rescale 함수와 요약통계 함수를 직접 작성해 봄으로써, 함수 작성 과정을 실습해 볼 수 있도록 구성되어 있다.

  1. 해들리 위컴이 함수의 필요성과 중요성을 언급하며 제시한 사례를 가져왔다. 자세한 사항은 R for Data Science 2판 26장 함수를 참고한다.↩︎