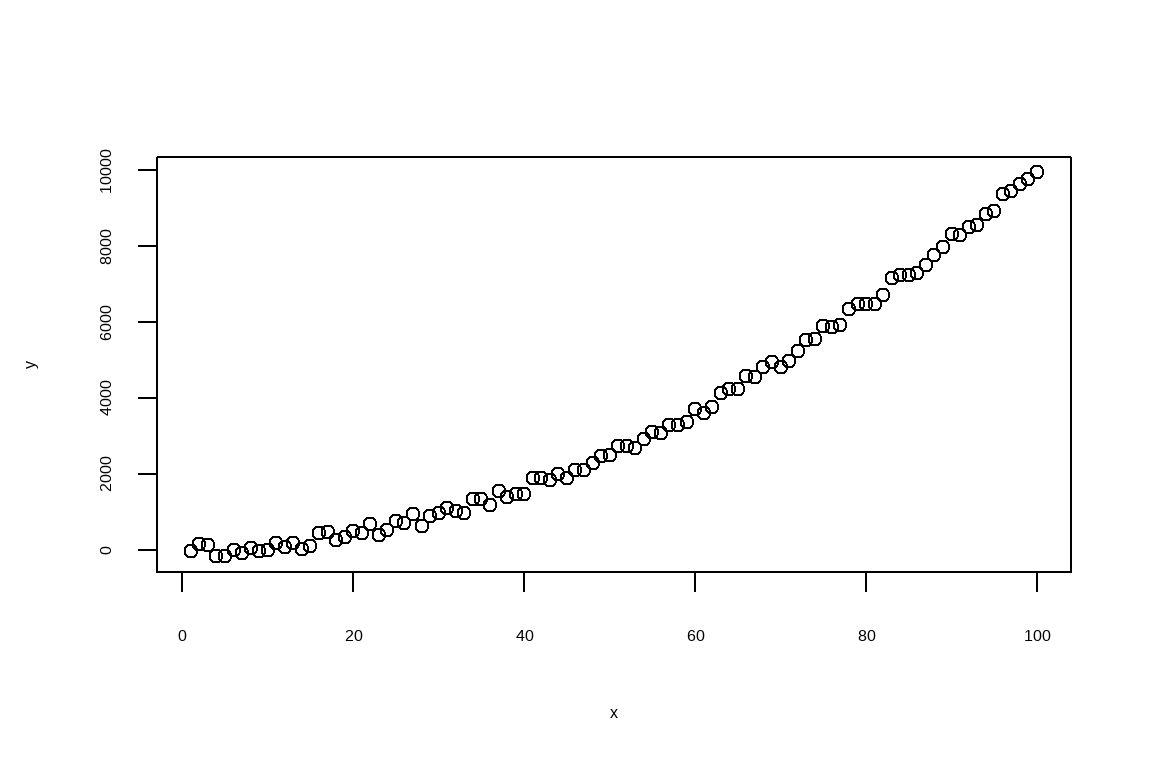모형 개발의 목표는 정보를 잃지 않고 데이터셋을 간단히 요약하는 것이다. 모형은 참 ‘신호’(즉, 관심 있는 현상으로 생성된 패턴)를 포착하고 ‘잡음’(즉, 관심 없는 임의 변동)을 구분하여 신호 대비 잡음비를 최적화한다. 전통적으로 모형은 추론 혹은 가설이 사실인지 검증하고 확인하는 데 중점을 둔다. 추정과 가설 검정 작업은 복잡하지는 않지만 어렵다. 모형 제작의 목표는 진실을 찾는 것보다는 유용하지만 단순한 근사치를 찾아내는 것이다.
11.1 회귀분석
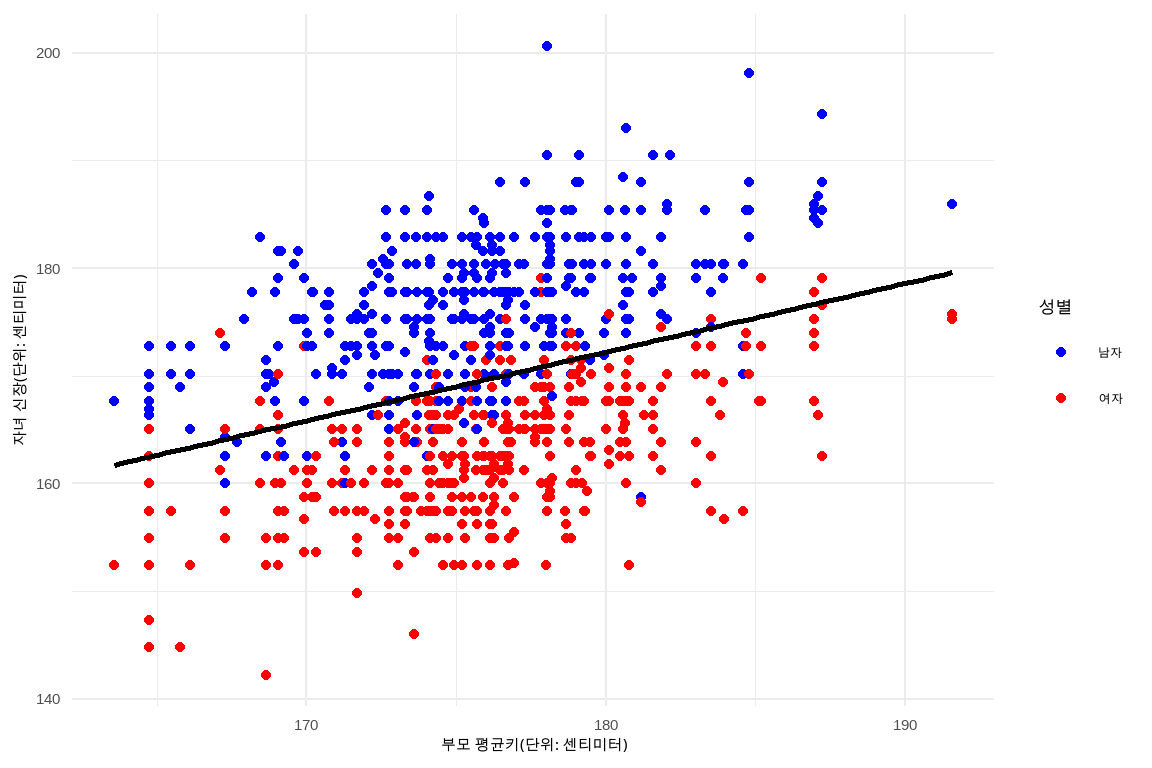
회귀분석은 갤톤(Galton)의 부모와 자식의 신장 간의 관계를 회귀식으로 표현한 데이터셋(Caffo 2015)(Friendly 2023)이 유명하다. 부모의 신장을 기초로 자녀의 신장을 예측하는 회귀식을 구하기 전에 산점도를 통해 관계를 살펴보면 다음과 같다.
먼저 dataframe 자료형을 as_tibble() 함수로 변환하고, 신장 단위를 인치에서 cm로 변환한다. 영어로 된 성별을 ifelse 함수로 남자와 여자로 변환한 후 ggplot으로 시각화한다. geom_smooth() 함수로 회귀직선을 추가한다.
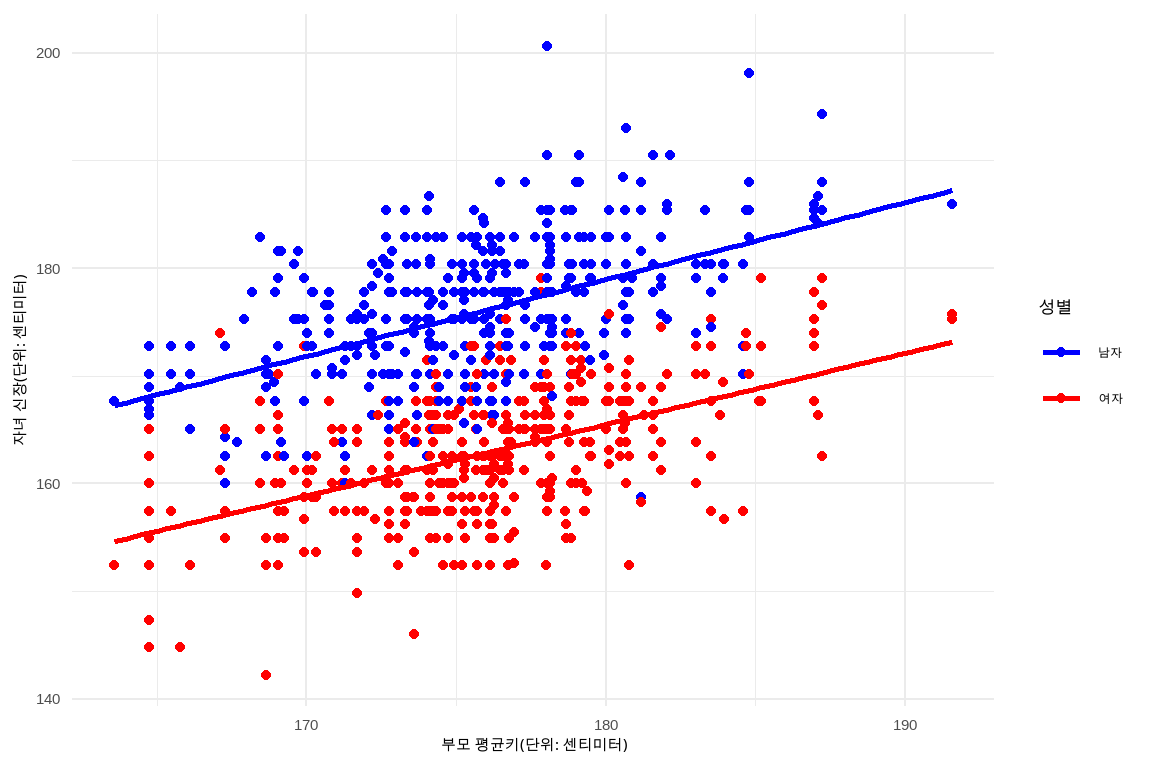
동일한 galton_tbl 데이터를 사용하여 부모의 평균 키와 자녀의 신장 간의 관계를 성별로 시각화한다. 성별에 따라 점의 색상을 다르게 표시하고, 성별에 따른 별도의 선형 회귀선을 추가한다. x축과 y축의 레이블을 설정하고, 성별에 따라 점의 색상을 남자는 파란색, 여자는 붉은색으로 수동 설정한다.
galton_tbl|>ggplot(aes(midparentHeight, childHeight))+geom_point(aes(colour=gender))+geom_smooth(aes(group =gender, color =gender), method="lm", se =FALSE)+labs( x ="부모 평균키(단위: 센티미터)", y ="자녀 신장(단위: 센티미터)", color ="성별")+scale_color_manual(values =c("남자"="blue", "여자"="red"))
그림 11.2: 성별에 따른 산점도와 회귀직선
조지 박스(George Box) 박사 명언
모든 모델은 틀렸지만, 어떤 모델은 유용하다. (All models are wrong, but some are useful.)
자연과학과 사회과학의 두 가지 사례를 통해 조지 박스 박사의 모형에 대한 명언을 되새겨보자. 지구의 움직임을 설명하기 위한 기본 모형은 “평평한 지구” 모형으로, 지구의 실제 구조와 움직임을 정확히 반영하지 못했지만, 일상적인 생활에서 지구의 특성을 설명하기에는 충분했다. 경제학에서 사용되는 많은 모형은 단순화된 가정을 바탕으로 한다. 예를 들어, 모든 소비자와 생산자가 완벽한 정보를 가지고 있고 합리적으로 행동한다는 가정을 바탕으로 한 경제 모형은 현실 세계의 복잡한 상황을 반영하지 않지만, 복잡한 경제 관계를 단순화시켜 기본적인 경제 원리를 이해시키는 데 도움이 된다.
11.2 회귀계수 추정
선형대수로 회귀계수를 추정하는 문제를 풀면 다음과 같이 정의된다. 한 번 미분해서 \(\nabla f(\beta ) = -2Xy + X^t X \beta =0\) 이 되고, 0으로 놓고 푼 값은 최솟값이 되는데, 그 이유는 \(\beta\)에 대해서 두 번 미분하게 되면 \(2 X^t X\) 로 양수가 되기 때문이다.
\[f(\beta ) = ||y - \beta X ||^2 = (y - \beta X)^t (y - \beta X) = y^t y - 2 y^t X^t \beta + \beta^t X^t X \beta\]
\[\nabla f(\beta ) = -2Xy + X^t X \beta\]
\[\beta = (X^t X)^{-1} X^t y \]
위에서 정의된 방식으로 수식을 정의하고 이를 R로 코딩하면 회귀계수를 다음과 같이 구할 수 있다.
x<-galton_tbl$midparentHeighty<-galton_tbl$childHeightx<-cbind(1, x)solve(t(x)%*%x)%*%t(x)%*%y#> [,1]#> 57.4960510#> x 0.6373609
이를 lm 함수를 사용해서 다시 풀면 위에서 선형대수 수식으로 계산한 것과 동일함을 확인할 수 있다.
데이터 과학 분야의 제품 개발 방식은 다양하다. 엔지니어링의 관점에서 볼 때, 전통적인 장인의 기술이 제자에게 계승되는 방식에서 시작하여, 포드의 대량 생산 방식을 거치고, 대량 맞춤생산(Mass Customization) 방식으로 발전하여, 현재에는 기계 학습과 딥러닝이 통합된 혁신적인 개발 방식까지 다양한 방법론이 혼재되어 있다.
전통적인 가내수공업 방식은 개별 주문에 따라 제품을 최적화하여 만드는 방식이다. 이 방식에서는 인간의 경험과 지식이 중요한 역할을 하며, 고객의 특별한 요구사항을 충족하기 위해 맞춤형 모델을 개발한다. 이러한 방식을 간략히 살펴보면, 각 고객의 고유한 필요에 따라 제품이나 서비스를 특별히 설계하고 생산하는 것이 핵심이다.
이번 장에서는 전통적인 통계모형을 제작하는 과정을 살펴보고 12장에서 다른 방식의 모형개발과정을 살펴본다.
데이터 준비 단계에서 모의시험 데이터를 생성한다. 독립변수 \(x\)는 1부터 100까지의 연속적인 수열이며, 종속변수 \(y\)는 \(x^2\)에 노이즈를 추가한 값으로 정의한다. 생성된 데이터는 df라는 데이터프레임에 저장하며, 데이터의 처음 몇 행을 출력하여 확인한다.
탐색적 데이터 분석(EDA) 단계에서는 데이터의 기술통계량을 psych 패키지의 describe 함수를 활용하여 출력하고, 데이터 분포와 관계를 확인하기 위해 \(x\)와 \(y\)의 산점도로 시각화한다.
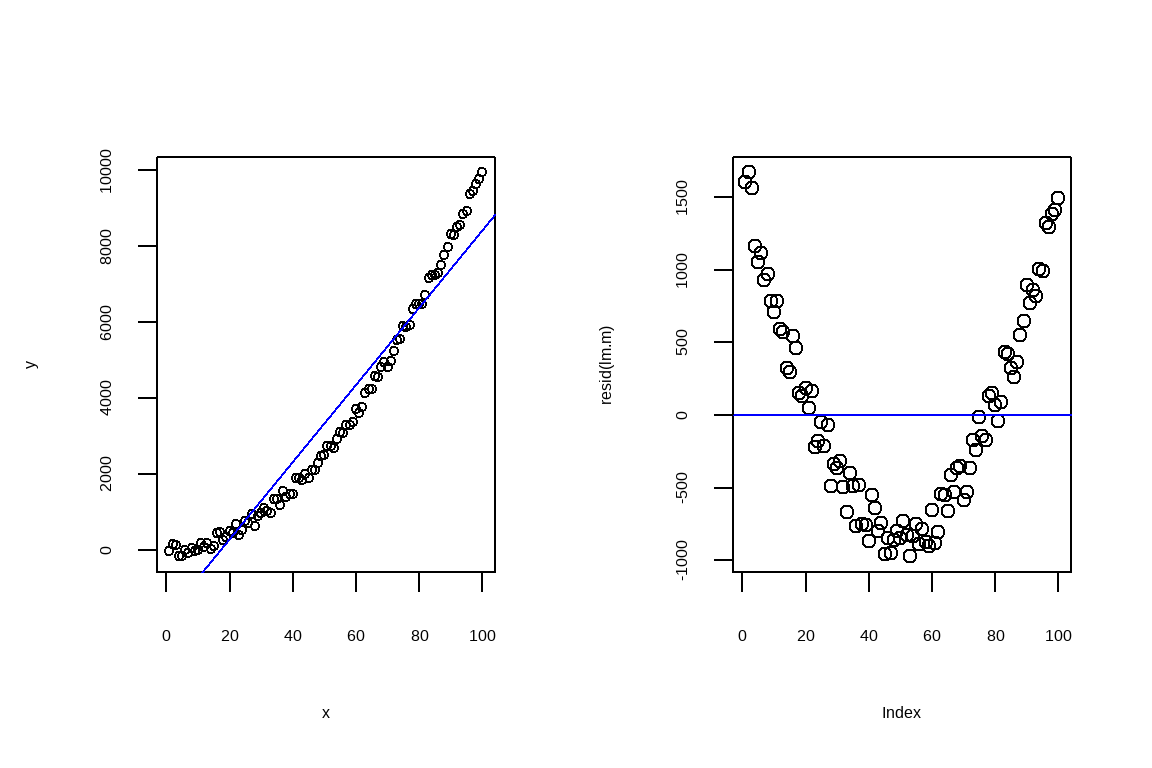
모형 적합 단계에서는 먼저, 선형회귀 모델을 사용하여 \(y\)를 \(x\)로 예측한다. 적합된 선형 모형 결과를 출력하고, 적합된 모델과 잔차를 시각적으로 확인한다. \(y = \beta_0 + \beta_1 x + \beta_2 x^2\) 형태를 가진 2차 회귀 모형을 적합시킨다. \(x^2\) 항을 데이터프레임에 추가하여 2차 회귀 모델을 적합한 후, 결과를 출력하고, 적합된 모형과 잔차를 시각적으로 확인한다. 기본모형과 최종모형 사이에는 수많은 가설생성과 검증 절차가 진행되어 데이터를 가장 잘 설명하는 모형을 최종 선택하게 된다.
##========================================================## 01. 데이터 준비##========================================================## 모의시험 데이터 생성x<-seq(1, 100, 1)y<-x**2+jitter(x, 1000)df<-tibble(x,y)head(df)#> # A tibble: 6 × 2#> x y#> <dbl> <dbl>#> 1 1 -22.5 #> 2 2 148. #> 3 3 143. #> 4 4 -153. #> 5 5 -167. #> 6 6 -1.99##========================================================## 02. 탐색적 데이터 분석##========================================================# 통계량psych::describe(df)#> vars n mean sd median trimmed mad min max range#> x 1 100 50.50 29.01 50.50 50.50 37.06 1.00 100.00 99.00#> y 2 100 3410.06 3042.91 2601.12 3125.51 3270.21 -167.36 9941.33 10108.69#> skew kurtosis se#> x 0.0 -1.24 2.90#> y 0.6 -0.95 304.29# 산점도plot(x, y)
그림 11.3: 데이터를 확인하는 단계
##========================================================## 03. 모형 적합##========================================================#---------------------------------------------------------# 3.1. 선형회귀 적합lm.m<-lm(y~x, data=df)summary(lm.m)#> #> Call:#> lm(formula = y ~ x, data = df)#> #> Residuals:#> Min 1Q Median 3Q Max #> -974.0 -656.3 -171.5 554.5 1672.1 #> #> Coefficients:#> Estimate Std. Error t value Pr(>|t|) #> (Intercept) -1727.20 150.10 -11.51 <2e-16 ***#> x 101.73 2.58 39.42 <2e-16 ***#> ---#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1#> #> Residual standard error: 744.9 on 98 degrees of freedom#> Multiple R-squared: 0.9407, Adjusted R-squared: 0.9401 #> F-statistic: 1554 on 1 and 98 DF, p-value: < 2.2e-16par(mfrow=c(1,2))# 적합모형 시각화plot(x,y, data=df, cex=0.7)abline(lm.m, col='blue')# 잔차 plot(resid(lm.m))abline(h=0, type='3', col='blue')
그림 11.4: 기본 모형 적합 후 적합도 확인
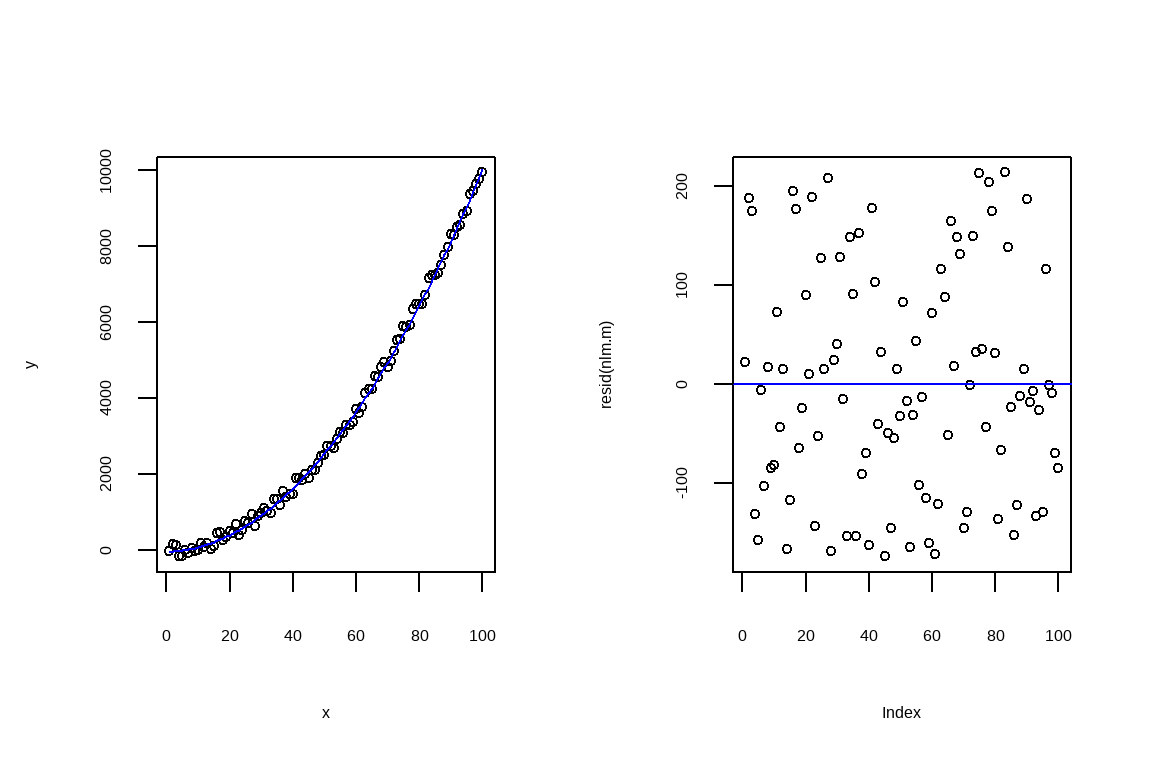
#---------------------------------------------------------# 3.2. 비선형회귀 적합# 비선형회귀적합df$x2<-df$x**2nlm.m<-lm(y~x+x2, data=df)summary(nlm.m)#> #> Call:#> lm(formula = y ~ x + x2, data = df)#> #> Residuals:#> Min 1Q Median 3Q Max #> -174.47 -94.06 -10.90 89.63 213.36 #> #> Coefficients:#> Estimate Std. Error t value Pr(>|t|) #> (Intercept) -48.64546 35.52775 -1.369 0.1741 #> x 2.98939 1.62371 1.841 0.0687 . #> x2 0.97761 0.01558 62.765 <2e-16 ***#> ---#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1#> #> Residual standard error: 116.1 on 97 degrees of freedom#> Multiple R-squared: 0.9986, Adjusted R-squared: 0.9985 #> F-statistic: 3.398e+04 on 2 and 97 DF, p-value: < 2.2e-16par(mfrow=c(1,2))# 적합모형 시각화plot(x, y, data=df, cex=0.7)lines(x, fitted(nlm.m), col='blue')# 잔차 plot(resid(nlm.m), cex=0.7)abline(h=0, type='3', col='blue')
그림 11.5: 최종모형과 적합도 검증
predict와 forecast 차이
predict와 forecast는 둘 다 ’예측하다’라는 의미로 사용되지만, 차이는 명확하다. predict는 보다 확정적인 결과에 대한 예측에 초점을 맞추는 반면, forecast는 미래의 불확실한 사건에 대한 확률적인 추정에 중점을 둔다.
predict는 과학, 사회학, 심리학 등에서 사용되며 일반적으로 특정 사건이나 결과가 일어날 것이라고 말하는 데 사용된다. 예를 들어, 기계학습 모형이 특정 데이터를 바탕으로 결과를 ’예측(predict)’하는 경우가 대표적이다. 특정 조건이나 상황에서 특정 결과가일어날 것이라고 하는, 비교적 구체적이고 확정적인 예측을 내포한다.
반면, forecast는 주로 기상학, 경제학, 재무학 등에서 사용되며, 미래의 사건이나 조건에 대한 확률적인 추정을 의미한다. forecast는 불확실성과 확률적인 요소를 포함한 예측을 가리키며, 예를 들어 날씨 예보나 경제 성장률 예측 등에서 사용되기 때문에 특정 사건이 발생할 ’가능성’이나 ’확률’을 중시한다.
11.4 요약
모형은 복잡한 현실 세계를 추상화하고 단순화하여 현상의 본질을 이해하는 데 도움을 준다. 갤톤의 부모와 자식의 신장 데이터를 통해 회귀분석이라는 강력한 도구를 사용하여 변수 간의 관계를 파악하는 방법을 배웠다.
데이터 준비, 탐색적 데이터 분석, 모형 적합의 단계를 거치며 최적의 모형을 찾아가는 과정은 데이터 과학자에게 있어 핵심적인 역량이다. 이 과정에서 우리는 도메인 지식과 통계학적 지식을 동원하여 데이터를 이해하고, 가설을 세우고 검증하며, 모형의 성능을 평가하고 개선해 나간다.
모형 구축은 단순히 주어진 데이터에 알고리즘을 적용하는 것 이상의 의미를 갖는다. 현실에 대한 이해를 바탕으로, 데이터에 담긴 정보를 추출하고 새로운 통찰을 발견하는 지적 탐구의 과정이며 데이터로부터 학습한 모형을 활용하여 미래를 예측하고 의사결정을 지원함으로써 실질적인 가치를 창출할 수 있다.
앞으로 데이터 과학 분야가 빠르게 발전하고 그 영향력이 확대됨에 따라, 통계 모형의 역할도 더욱 커질 것으로 기대된다. 데이터 과학자로서 모형 구축 과정에서 맞닥뜨리는 도전 과제들을 슬기롭게 헤쳐나가는 한편, 모형의 한계를 인식하고 윤리적 책임을 다할 줄 아는 성숙한 자세를 갖추어야 할 것이다.
그림 11.1: 산점도와 회귀직선그림 11.2: 성별에 따른 산점도와 회귀직선그림 11.3: 데이터를 확인하는 단계그림 11.4: 기본 모형 적합 후 적합도 확인그림 11.5: 최종모형과 적합도 검증
Caffo, Brian. 2015. Advanced Linear Models for Data Science. Leanpub.
Friendly, Michael. 2023. HistData: Data Sets from the History of Statistics and Data Visualization.
