8 새로운 필드와 집계
탐험 기록을 주의 깊게 다시 읽은 후, 탐험대가 보고한 방사선 측정치를 5% 상향 조정해야 할 필요가 있음을 깨달았다. 저장된 데이터를 변경하기보다는, 쿼리의 일부로서 현장에서 계산을 수행할 수 있다.
SELECT 1.05 * reading FROM Survey WHERE quant = 'rad';| 1.05 * reading |
|---|
| 10.311 |
| 8.19 |
| 8.8305 |
| 7.581 |
| 4.5675 |
| 2.2995 |
| 1.533 |
| 11.8125 |
쿼리를 실행하면, 표현식 1.05 * reading이 각 행마다 평가된다. 표현식에는 임의의 필드, 통상 많이 사용되는 연산자, 그리고 다양한 함수를 사용할 수 있다. (정확하게는 어떤 데이터베이스 관리자를 사용되느냐에 따라 의존성을 띄게된다.) 예를 들어, 화씨로 된 온도 측정치를 섭씨로 변환하고 소수점 아래 둘째 자리에서 반올림할 수 있다.
SELECT taken, round(5 * (reading - 32) / 9, 2) FROM Survey WHERE quant = 'temp';| taken | round(5*(reading-32)/9, 2) |
|---|---|
| 734 | -29.72 |
| 735 | -32.22 |
| 751 | -28.06 |
| 752 | -26.67 |
예시에서 볼 수 있듯이, 방정식으로부터 생성된 새 필드를 설명하는 문자열은 매우 길고 복잡해질 수 있다. SQL에서 필드 이름을 바꾸는 것이 허용되는데, 계산된 필드든 데이터베이스 기존 필드든 상관없다. 간결함과 명확성을 위한 것이다. 예를 들어, 쿼리를 다음과 같이 작성할 수 있다:
SELECT taken, round(5 * (reading - 32) / 9, 2) as Celsius FROM Survey WHERE quant = 'temp';다른 필드의 값을 조합할 수도 있다. 예를 들어, 문자열 접합 연산자 (string concatenation operator, ||)를 사용한다.
SELECT personal || ' ' || family FROM Person;| personal |
|---|
| William Dyer |
| Frank Pabodie |
| Anderson Lake |
| Valentina Roerich |
| Frank Danforth |
first와 last 대신에 필드 이름으로 personal과 family를 사용하는 것이 이상해 보일지 모른다. 하지만, 문화적 차이를 다루기 위한 필요한 첫번째 단계다. 예를 들어, 다음 규칙을 고려해보자.
| 성명 전부(Full Name) | 알파벳 순서 | 이유 |
|---|---|---|
| Liu Xiaobo | Liu | 중국 성이 이름보다 먼저 온다. |
| Leonardo da Vinci | Leonardo | “da Vinci” 는 “from Vinci”를 뜻한다. |
| Catherine de Medici | Medici | 성(family name) |
| Jean de La Fontaine | La Fontaine | 성(family name)이 “La Fontaine”이다. |
| Juan Ponce de Leon | Ponce de Leon | 전체 성(full family name)이 “Ponce de Leon”이다. |
| Gabriel Garcia Marquez | Garcia Marquez | 이중으로 된 스페인 성(surnames) |
| Wernher von Braun | von or Braun | 독일 혹은 미국에 있는냐에 따라 달라짐 |
| Elizabeth Alexandra May Windsor | Elizabeth | 군주가 통치하는 이름에 따라 알파벳순으로 정렬 |
| Thomas a Beckett | Thomas | 시성된(canonized) 이름에 따라 성인이름 사용 |
분명하게, 심지어 ’personal’과 ’family’라는 두 부분으로 나누는 것만으로는 충분하지 않다.
8.1 합집합
UNION 연산자는 두 개의 쿼리 결과를 결합한다.
SELECT * FROM Person WHERE id = 'dyer' UNION SELECT * FROM Person WHERE id = 'roe';| id | personal | family |
|---|---|---|
| dyer | William | Dyer |
| roe | Valentina | Roerich |
UNION ALL 명령은 UNION 연산자와 동일하지만, UNION ALL은 모든 값을 선택한다는 점에서 차이가 있다. 차이점은 UNION ALL이 중복 행을 제거하지 않는다는 것이다. 대신, UNION ALL은 쿼리의 모든 행을 가져와서 하나의 테이블로 결합한다. UNION 명령은 결과 세트에 대해 SELECT DISTINCT를 수행한다. 만약 합병할 모든 레코드가 고유하다면, DISTINCT 단계를 건너뛰므로 더 빠른 결과를 얻기 위해 UNION ALL을 사용한다.
8.2 집계
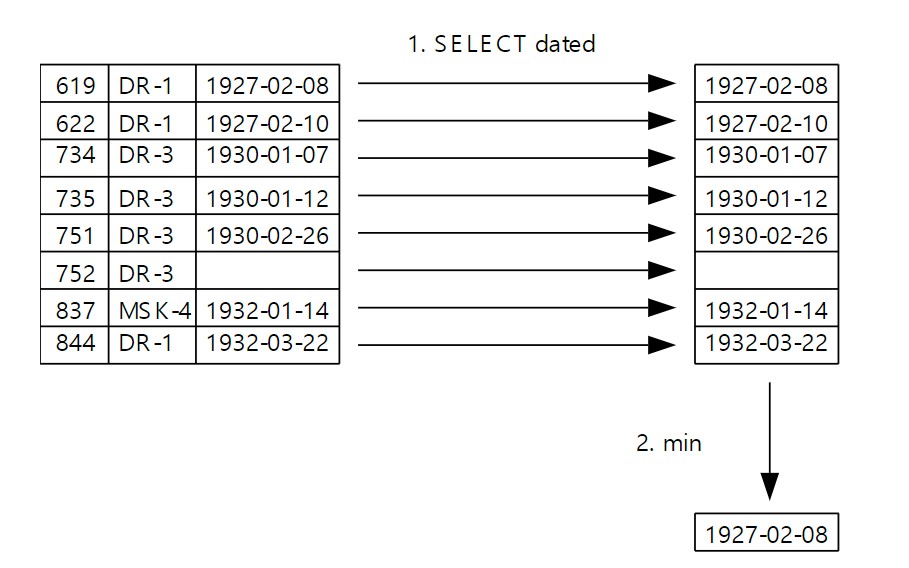
이제 데이터의 평균과 범위를 계산하고자 한다. Visited 테이블에서 모든 날짜 정보를 어떻게 선택하는지 알고 있다.
SELECT dated FROM Visited;| dated |
|---|
| 1927-02-08 |
| 1927-02-10 |
| 1930-01-07 |
| 1930-01-12 |
| 1930-02-26 |
| -null- |
| 1932-01-14 |
| 1932-03-22 |
하지만 조합하기 위해서는 min 혹은 max 같은 집계 함수(aggregation function)를 사용해야만 한다. 각 함수는 입력으로 레코드 집합을 받고 출력으로 단일 레코드를 만든다.
SELECT min(dated) FROM Visited;| min(dated) |
|---|
| 1927-02-08 |
SELECT max(dated) FROM Visited;| max(dated) |
|---|
| 1932-03-22 |
min과 max는 SQL에 내장된 단지 두개의 집계 함수다. 다른 함수로 많이 사용되는 avg, count, sum을 들 수 있다.
SELECT avg(reading) FROM Survey WHERE quant = 'sal';| avg(reading) |
|---|
| 7.20333333333333 |
SELECT count(reading) FROM Survey WHERE quant = 'sal';| count(reading) |
|---|
| 9 |
SELECT sum(reading) FROM Survey WHERE quant = 'sal';| sum(reading) |
|---|
| 64.83 |
여기서 count(reading)을 사용했다. 테이블에서 quant나 다른 필드를 세는 것도 마찬가지로 쉽게 할 수 있다. 심지어 count(*)를 사용할 수도 있다. 이 함수는 값 자체에 대해서는 관심이 없고, 값이 몇 개 있는지만을 고려하기 때문이다.
SQL에서 한 번에 여러 집계작업을 수행할 수도 있다. 예를 들어, 적절한 염분측정치의 범위를 찾을 수도 있다.
SELECT min(reading), max(reading) FROM Survey WHERE quant = 'sal' AND reading <= 1.0;| min(reading) | max(reading) |
|---|---|
| 0.05 | 0.21 |
출력결과가 놀라움을 줄 수도 있지만, 원 결과값과 집계 결과를 조합할 수도 있다.
SELECT person, count(*) FROM Survey WHERE quant = 'sal' AND reading <= 1.0;| person | count(*) |
|---|---|
| lake | 7 |
Lake의 이름이 Roerich나 Dyer 대신 나타나는 이유는 무엇일까? 이는 데이터베이스 관리자가 특정 필드를 집계해야 하지만, 집계 방법에 대한 지시가 없을 때 실제 입력 세트에서 하나의 값을 선택하기 때문이다. 이는 처리된 첫 번째 값일 수도 있고, 마지막 값이나 전혀 다른 어떤 값일 수도 있다.
이 쿼리의 경우, person 필드가 그룹화되지 않았기 때문에, 데이터베이스 관리자는 person 칼럼에 대해 어떤 특정 값을 선택한다. 그 결과로 ’lake’가 출력된 것일 수 있는데, 이는 ’lake’가 데이터베이스에서 처리된 첫 번째 또는 마지막 값일 가능성이 있다. 데이터베이스의 내부 작동 방식에 따라, 이러한 선택은 일관성이 없을 수도 있다.
또 다른 중요한 사실은 집계할 값이 없을 때 — 예를 들어, WHERE 절을 만족하는 행이 없는 경우 — 집계의 결과는 “모른다”로 처리되며, 이는 0이나 다른 임의의 값이 아니라는 점이다.
예를 들어, 특정 조건을 만족하는 행이 하나도 없다면, count() 함수와 같은 집계 함수는 0을 반환하지만, sum()이나 avg()와 같은 다른 집계 함수들은 NULL을 반환할 수 있다. 이는 해당 집계 함수가 적용될 데이터가 전혀 없기 때문에, 그 결과가 “알 수 없는 값”이 됨을 의미한다. 이러한 방식은 데이터의 부재가 잘못된 결과로 이어지는 것을 방지하는 데 도움이 된다.
| person | max(reading) | sum(reading) |
|---|---|---|
| -null- | -null- | -null- |
집계 함수의 또 다른 중요한 특징은 SQL 나머지 부분과는 매우 유용한 방식으로 일관성이 없다는 것이다. 이러한 동작은 다음과 같은 쿼리를 작성할 수 있게 해준다:
집합 함수의 마지막 중요한 한가지 기능은 매우 유용한 방식으로 나머지 SQL과는 일관되지 않다는 점이다. 두 값을 더할 때 하나가 null이면 결과는 null이 된다. 이를 확장하면, sum을 사용하여 집합의 모든 값을 더하고 그 값들 중 하나라도 null이라면 결과도 null이 되어야 한다. 그러나 집계 함수가 null 값을 무시하고 null이 아닌 값들만 결합하는 것이 훨씬 더 유용하다. 명시적으로 항상 필터해야하는 대신에 이것의 결과 쿼리를 다음과 같이 작성할 수 있게 한다.
SELECT min(dated) FROM Visited;| min(dated) |
|---|
| 1927-02-08 |
명시적으로 항상 다음과 같이 필터하는 쿼리를 작성할 필요가 없다.
SELECT min(dated) FROM Visited WHERE dated IS NOT NULL;| min(dated) |
|---|
| 1927-02-08 |
모든 레코드를 한꺼번에 집계하는 것이 항상 의미 있는 것은 아니다. 예를 들어, 데이터에 체계적인 편향(bias)이 있을 것이라고 의심하고, 일부 과학자들의 방사능 측정값이 다른 사람들보다 높다고 생각한다고 가정해보자. 이런 경우에 다음과 같은 방법은 효과적이지 않다:
SELECT person, count(reading), round(avg(reading), 2)
FROM Survey
WHERE quant = 'rad';| person | count(reading) | round(avg(reading), 2) |
|---|---|---|
| roe | 8 | 6.56 |
데이터베이스 관리자가 각 과학자별로 별도로 집계하는 대신 임의로 한 과학자의 이름을 선택하기 때문에 이 방법은 효과적이지 않다. 과학자가 단지 다섯 명뿐이므로, 다음 형식의 다섯 개의 쿼리를 작성할 수 있다.
SELECT person, count(reading), round(avg(reading), 2)
FROM Survey
WHERE quant = 'rad'
AND person = 'dyer';| person | count(reading) | round(avg(reading), 2) |
|---|---|---|
| dyer | 2 | 8.81 |
하지만, 이러한 접근법은 성가시고, 만약 50명 혹은 500명의 과학자를 가진 데이터셋을 분석한다면, 모든 쿼리를 올바르게 작성할 가능성은 작다.
필요한 것은 데이터베이스 관리자에게 각 과학자별로 시간을 별도로 집계하도록 GROUP BY 절을 사용하여 지시하는 것이다.
SELECT person, count(reading), round(avg(reading), 2)
FROM Survey
WHERE quant = 'rad'
GROUP BY person;| person | count(reading) | round(avg(reading), 2) |
|---|---|---|
| dyer | 2 | 8.81 |
| lake | 2 | 1.82 |
| pb | 3 | 6.66 |
| roe | 1 | 11.25 |
GROUP BY는 그 이름이 암시하는 것처럼 정확히 다음과 같이 동작한다. 지정된 필드의 같은 값을 가진 모든 레코드를 그룹화하여 집계가 각 배치를 별도로 처리할 수 있도록 한다. 각 배치에 모든 레코드는 person에 대해 동일한 값을 가지기 때문에, 데이터베이스 관리자가 임의의 값을 잡아서 집합된 reading 값과 함께 표시하는 것은 더 이상 문제가 되지 않는다.
우리가 한 번에 여러 기준에 따라 정렬할 수 있는 것처럼, 다중 기준에 따라 그룹화할 수도 있다. 예를 들어, 과학자별 및 측정된 양별로 평균 측정값을 얻기 위해서 GROUP BY 절에 다른 필드를 추가하기만 하면 된다.
SELECT person, quant, count(reading), round(avg(reading), 2)
FROM Survey
GROUP BY person, quant;| person | quant | count(reading) | round(avg(reading), 2) |
|---|---|---|---|
| -null- | sal | 1 | 0.06 |
| -null- | temp | 1 | -26.0 |
| dyer | rad | 2 | 8.81 |
| dyer | sal | 2 | 0.11 |
| lake | rad | 2 | 1.82 |
| lake | sal | 4 | 0.11 |
| lake | temp | 1 | -16.0 |
| pb | rad | 3 | 6.66 |
| pb | temp | 2 | -20.0 |
| roe | rad | 1 | 11.25 |
| roe | sal | 2 | 32.05 |
quant를 표시되는 필드 목록에 추가한 것에 주목하자. 그렇지 않으면 결과가 큰 의미를 가지지 않을 것이다.
한 단계 더 나아가 측정을 수행한 사람을 알 수 없는 모든 항목을 제거해보자.
SELECT person, quant, count(reading), round(avg(reading), 2)
FROM Survey
WHERE person IS NOT NULL
GROUP BY person, quant
ORDER BY person, quant;| person | quant | count(reading) | round(avg(reading), 2) |
|---|---|---|---|
| dyer | rad | 2 | 8.81 |
| dyer | sal | 2 | 0.11 |
| lake | rad | 2 | 1.82 |
| lake | sal | 4 | 0.11 |
| lake | temp | 1 | -16.0 |
| pb | rad | 3 | 6.66 |
| pb | temp | 2 | -20.0 |
| roe | rad | 1 | 11.25 |
| roe | sal | 2 | 32.05 |
좀더 면밀하게 살펴보면, 이 쿼리는,
Survey테이블에서person필드가null이 아닌 레코드를 선택한다.상기 레코드를 부분집합으로 그룹지어서 각 부분집합의
person과quant의 값은 같다.먼저
person으로 부분집합을 정렬하고나서quant로 각 하위 그룹내에서도 정렬한다.각 부분집합의 레코드 숫자를 세고, 각각
reading평균을 계산하고, 각각person과quant값을 선택한다. (모두 동등하기 때문에 어느 것인지는 문제가 되지 않는다.)
연습문제
객관식
- 문제: SQL에서 새로운 계산된 필드를 만들 때 어떤 키워드를 사용합니까?
CREATECALCULATEASDEFINE
- 문제: 다음 중 집계 함수(aggregation function)는 무엇입니까?
JOINGROUP BYSUMORDER BY
- 문제:
GROUP BY절을 사용하는 주된 목적은 무엇입니까?- 데이터베이스의 보안 강화
- 레코드 정렬
- 지정된 열 기준으로 레코드 그룹화
- 중복 레코드 제거
염도 측정치 수정
추가로 정보를 살펴본 결과, 발렌티나 로에리히(Valentina Roerich)가 염도를 백분율로 보고했다는 것을 알게 되었다. Survey 테이블에서 모든 염도 측정치를 100으로 나눈 값으로 반환하는 쿼리를 작성하시오.
통합 측정목록
UNION을 사용하여 발렌티나 로에리히(Roerich가)의 염도 측정치를 앞선 도전과제에서 설명한 대로 수정하고, 발렌티나 로에리히만의 측정치로 통합된 염도 측정치 목록을 만든다. 출력 결과는 다음과 같아야 한다.
| taken | reading |
|---|---|
| 619 | 0.13 |
| 622 | 0.09 |
| 734 | 0.05 |
| 751 | 0.1 |
| 752 | 0.09 |
| 752 | 0.416 |
| 837 | 0.21 |
| 837 | 0.225 |
주요 사이트 식별자
Visited 테이블의 사이트 식별자는 ’-’로 구분된 두 부분으로 이루어져 있다.
SELECT DISTINCT site FROM Visited;| site |
|---|
| DR-1 |
| DR-3 |
| MSK-4 |
일부 주요 사이트 식별자(즉, 문자 코드)는 두 글자 길이이고 일부는 세 글자 길이이다. “문자열 내” 함수인 instr(X, Y)는 문자열 X 내에서 문자열 Y가 처음 나타나는 1-기반 인덱스를 반환하며, X 안에 Y가 존재하지 않으면 0을 반환한다. 부분 문자열 함수 substr(X, I, [L])는 X의 I 인덱스에서 시작하는 부분 문자열을 반환하며, 선택적으로 길이 L을 지정할 수 있다. 이 두 함수를 사용하여 고유한 주요 사이트 식별자 목록을 생성한다. (이 데이터의 경우, 목록은 “DR”과 “MSK”만을 포함해야 한다).
온도 측정횟수 세기
프랭크 파보디(Frank Pabodie)가 기록한 온도 측정횟수는 몇 번이며, 그 평균 값은 얼마인가?
NULL 포함 평균 계산
집합 값의 평균은 값들의 합을 값들의 개수로 나눈 것이다. 이는 avg 함수가 1.0, null, 5.0이라는 값들이 주어졌을 때 2.0 또는 3.0을 반환한다는 것을 의미하는가?
쿼리 의미는?
각 개별 방사능 측정값과 모든 방사능 측정값의 평균 사이의 차이를 계산하고자 한다. 이를 위해 다음과 같은 쿼리를 작성했다.
SELECT avg(reading) FROM Survey WHERE quant='rad';쿼리가 실제로 어떤 결과를 생성하며, 그 이유는 무엇일까?
group_concat 함수 사용
group_concat(field, separator) 함수는 지정된 구분자 문자(또는 구분자가 지정되지 않은 경우 ‘,’)를 사용하여 필드의 모든 값을 연결한다. 이를 사용하여 과학자들의 이름을 한 줄 목록으로 생성하면 출력결과는 다음과 같다.
William Dyer, Frank Pabodie, Anderson Lake, Valentina Roerich, Frank Danforth쉼표로 구분된 모든 과학자들의 성을 나열하는 쿼리를 작성하세요. 쉼표로 구분된 모든 과학자들의 개인 이름과 성을 나열하는 쿼리를 작성하세요.