18 . 암화화 프로토콜
18.3 페루 동전 던지기
페루 동전 던지기
이진수 표현(활동 1, 점을 세다), 패러티 개념(활동 4, 카드 뒤집기 마술)을 배우고, 활동 14 관광 마을에 일방향 함수 사례를 봤다면, 학생들이 이번활동을 통해서 좀더 많은 것을 얻어갈 것이다.
18.3.1 들어가며
이번 활동은 저작자 중의 한명이 페루에 있는 학생과 함께 작업할 때 최초로 고안되었다. (본 활동 제목 이름이 유래된 연유) 지역적인 상황에 맞추어 스토리를 각색할 수 있다.
결승전을 치를 홈구장을 어디로 할지 페루 리마(Lima)와 쿠스코(Cuzco) 축구팀이 결정해야 한다. 가장 단순한 방법은 동전 던지기다. 하지만 두 도시가 너무 떨어져 있다. 그리고, 리마팀을 대표하는 알리시아(Alicia)와 쿠스코팀을 대표하는 베니토(Benito)는 동전 던지러 함께 모일 시간과 예산이 없다. 통신선을 통해서 동전 던지기를 할 수 있을까? 알리시아가 동전을 던지고, 베니토가 동전 앞면 혹은 뒷면을 맞춘다. 하지만, 이 방식은 문제가 있다. 만약 베니토가 앞면하면, 알리시아는 간단하게 “미안해 친구, 뒷면이야”라고 하면 끝이다. 알리시아가 원래 부정직하지는 않지만, 매우 중요한 경기이고, 유혹을 참을 수는 없을 것이다. 설사 알리시아가 진실된다고 하더라도, 베니토가 불리한 상황이면 동전던지기 결과를 믿을 수 있을까?
이것이 두 사람이 결정해야 되는 사항이다. 공동으로 작업해서, 다음에 설명되는 and-게이트와 or-게이트로 구성된 회로를 설계한다. 실무에서 조금 지루한 것이 될 수 있지만, 원칙적으로 통신선을 통해 설계를 수행해야 한다. (전자우편도 또한 가능하다.) 구축 과정에서, 두 사람 모두 회로가 충분한 복잡성을 지녀서 상대방이 속일수 없도록 확실히 하는데 관심이 있다. 최종 회로는 공공 지식이 된다.
18.3.2 토론
and-게이트와 or-게이트 규칙은 단순하다. 게이트(gate) 각각은 두개 입력과 한개 출력으로 구성된다. 각 입력은 0 혹은 1 이 될 수 있고, 거짓(false)과 참(true)으로 각각 해석된다. 만약 두 입력이 모두 1 (참)이면, and-게이트 출력은 1 (참), 그렇지 않으면 0 (거짓)이 된다. 예를 들어, and-게이트에 입력으로 1과 0이 주어지면, 출력은 0이 된다. 만약 입력값 중 하나 혹은 둘 모두 1(참) 이면, or-게이트의 출력은 1(참)이 되고, 만약 입력이 모두 0 이면, 출력은 0(거짓)이 된다.
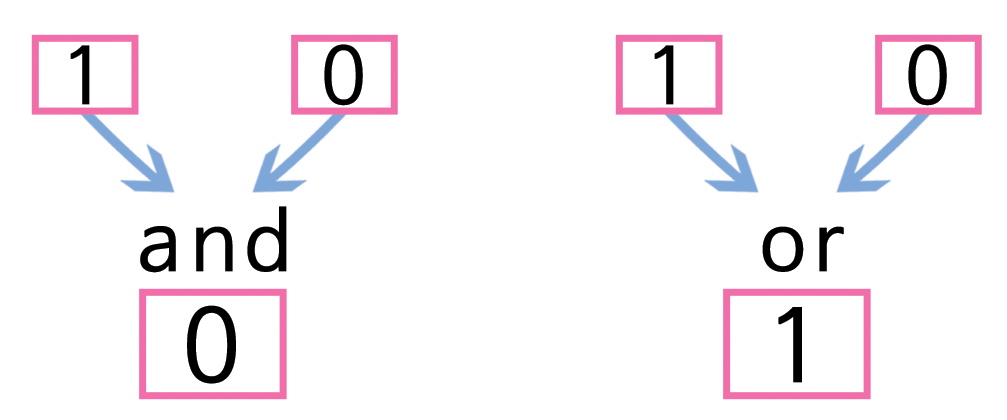
AND OR 게이트 I
한 게이트의 출력은 또 다른 (혹은 다른 몇개) 게이트의 입력이 되어 좀더 복잡한 효과를 만들어 낸다. 예를 들어, 왼쪽 회로에서 두개 or-게이트 출력은 세번째 or-게이트 입력과 연결된다. 만약 입력 4개 중의 어느 것이라도 1 이면, 출력은 1 이 되는 효과가 있다. 오른쪽 회로에서 상단 두개 and-게이트 각각의 출력은 아래 두개의 게이트에 입력값이 된다. 그래서 전체 회로는 출력으로 두개 값이 있다.
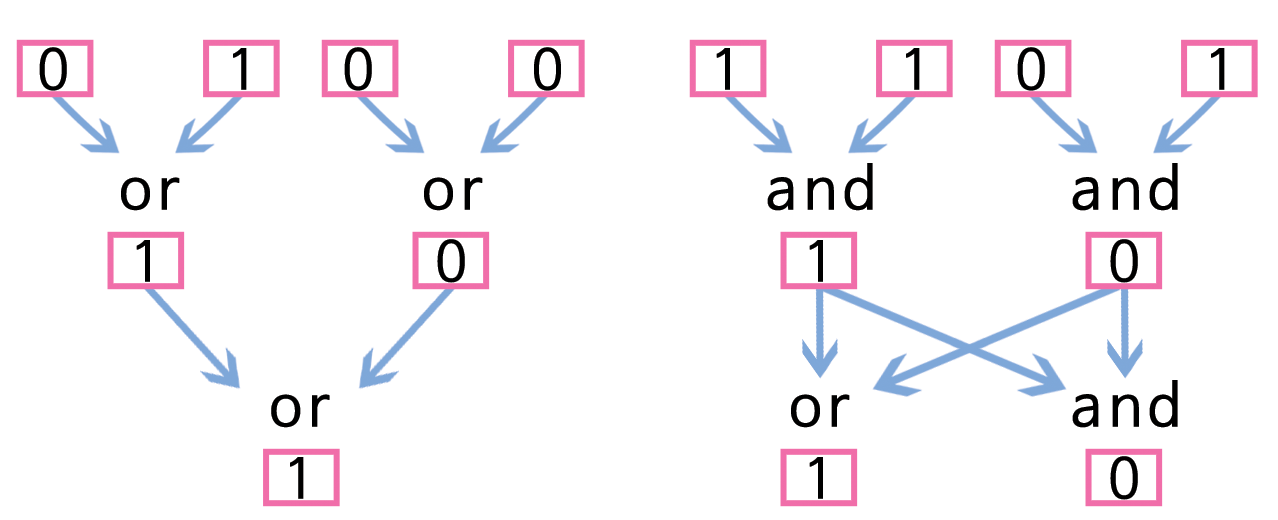
AND OR 게이트 II
페루 동전 던지기에는 좀더 복잡한 회로가 필요하다. 워크쉬트 회로는 6개 입력과 6개 출력이 있다. 다음에 한 입력 집합에 대한 해답이 있다.
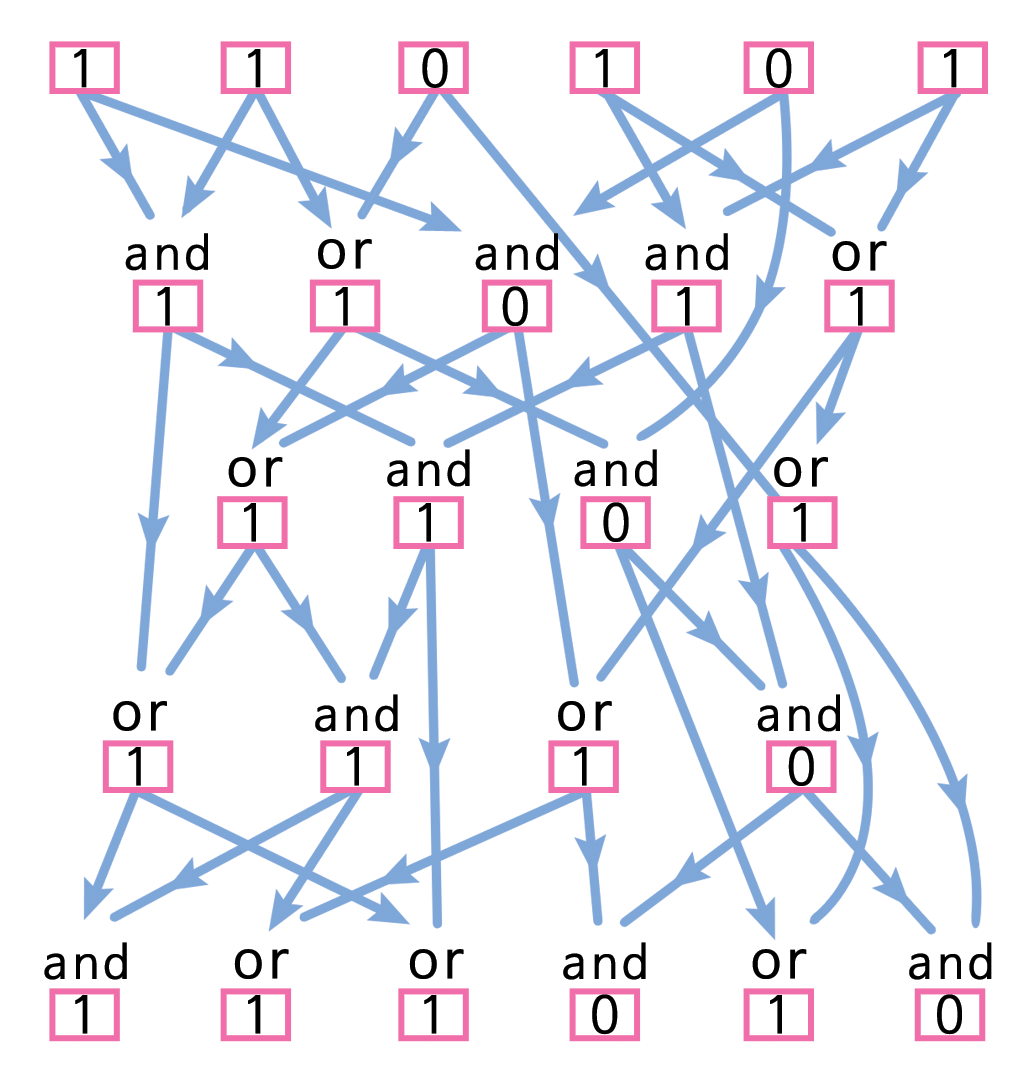
AND OR 게이트 III
통신선으로 회로를 동전 던지기에 사용하는 방식은 다음과 같다. 알리시아가 회로에 사용할 입력값으로 난수를 선택한다. 입력 난수는 6자리 이진수 (0 혹은 1)로 구성되어 있고, 비밀로 간직한다. 6자리 숫자를 회로에 넣어 베니토에게 6 비트 출력을 송부한다. 베니토가 출력값을 갖자 마자, 알리시아의 입력이 홀수인지 짝수인지 추축해야 한다— 다른 말로, 알리시아 입력값의 패리티( parity)를 추측해야 한다. 만약 회로가 충분히 복잡하다면, 베니토는 정답을 추론할 수 없을 것이다. 따라서 베니토의 추측은 무작위 선택이 된다. (사실, 베니토는 동전을 던져 선택할 수도 있다.) 베니토의 추측이 맞다면, 베니토가 이겨서 결승전은 쿠스코가 된다. 베니토의 추측이 맞지 않다면, 알리시아가 이겨서 결승전은 리마가 된다. 베니토가 알리시아에게 추측한 것을 말하면, 알리시아는 비밀 입력값을 공개한다. 그래서 베니코는 비밀 입력값이 주장하는 출력값이 되는지 검증한다.
학생을 작은 그룹으로 나누고, 각 그룹에게 회로와 게임패 몇개를 나눠주고 활동스토리를 설명한다. 아마도 학생들이 경쟁학교와 동전던지기를 통해서 스포츠 경기 시합을 준비한다고 상상하면, 학생들에게 좀더 의미가 있을 것이다. 게임패 색깔 규칙을 정해라— 빨간색 0, 파란색 1 등. 그리고 나서, 학생들이 기억하기 좋게 워크쉬트 상단에 주석으로 적어둔다.
알리시아가 고른 숫자를 보여주려고, 학생들에게 입력값으로 게임패를 어떻게 놓는지 보여준다. 그리고 나서 and-게이트와 or-게이트 규칙을 설명한다. 규칙은 워크쉬트 하단에 요약되어 있다. (학생들이 게임패에 색칠을 했다고 생각한다.)
해당 결과값을 도출하기 위해서, 회로를 통과하는 법, 노드에 게임패를 놓는 법을 보여준다. 정확하게 수행되어야 하고, 주의가 필요하다; (학생들에게 주면 않되는) 다음 표는 의문이 생기는 경우 참고용으로 각 입력값에 대한 출력값 정보를 담고 있다.

입력 출력
- 이제 각 그룹에서 알리시아와 베니토 역할을 할 학생을 선발한다. 그룹을 반으로 나눠서 반쪽은 알리시아 그룹, 다른 반쪽은 베니토 그룹이 된다. 알리시아가 회로에 입력값으로 사용될 난수를 선택하고, 출력값을 계산하고, 베니토에게 말한다. 베니토는 입력값의 패리티를 추축한다. (짝수도 될 수 있고, 홀수도 될 수 있다.) 과정을 진행하면서 베니토의 추측값은 본질적으로 랜덤이라는 것이 명백하다. 알리시아가 모두에게 입력값이 무엇이었는지 말한다. 만약 알리시아가 올바른 패리티를 추측했다면 베니토가 이기게 된다. 알리시아가 회로에서 나온 올바른 출력값을 전달했는지 점검해서, 베니토는 알리시아가 선택한 입력값을 변경하지 않았는지 확인한다.
이 지점에서 동전던지기는 완료된다.
출력이 주어진 상태에서 베니토가 입력값을 알 수 있다면 속일 수 있다. 그래서 알리시아의 관심은 베니토가 속임수를 쓰지 못하도록 활동 14에서 토의한 회로 함수가 일방향(one-way)인지 확인하는 것이다. 일방향 함수는 만약 입력이 무엇인지 알고 있다면 출력을 계산하기는 쉬운 함수다. 하지만, 주어진 출력에 대해서 입력을 계산해 내는 것은 매우 어렵다.
만약 동일한 출력을 만들어 내는 상반대는 패러티 입력이 두개 있다면, 알리시아도 속일 수 있다. 베니토가 무슨 방식으로 추측을 하던지 관계없이, 알리시아는 입력값을 공개해서 베니토가 틀렸다는 것을 보여줄 수 있다. 따라서, 동일한 출력에 다른 여러 입력값이 매핑되지 않도록 확실히 하는 것이 베니토의 관심사가 된다.
- 알리시아 혹은 베니토가 속일 수 있는 방법을 학생들이 찾을 수 있는지 살펴보라. 표 첫번째 줄에 다른 입력 몇 개는 출력으로 010010을 만들어 낸다. 해당되는 입력값은 000001, 000011, 000101, … 된다. 따라서, 만약 알리시아가 출력을 010010 이라고 하면, 만약 베니토가 패리티가 짝수라고 추측한다면 입력으로 000001을 선택할 수 있고, 베니토가 홀수라고 추측한다면 000011로 입력을 정할 수 있다.
해당 회로를 가지고, 베니토가 속이기는 어렵다. 하지만, 만약 출력이 011000 이라면, 입력은 100010 이어야 한다— 다른 경우의 수는 없다(표로 바로 점검할 수 있다.) 그래서, 만약 알리시아가 가져온 숫자가 이 숫자라면, 베니토는 짝수 패리티로 추측할 수 있고 맞다는 것을 확인할 수 있다. 컴퓨터 시스템은 훨씬 더 많은 비트를 사용해서 경우의 수가 엄청 많다. (추가 비트는 경우의 수를 2대로 한다.)
- 각 그룹 학생들에게 자신만의 회로를 고안하게 한다. 알리시아가 속이기 쉬운 회로를 만들었느지, 베니토가 속이기 좋은 회로인지 살펴보자. 회로 입력이 반듯이 6개가 될 필요는 없다. 심지어 다른 입력, 출력 숫자도 가능하다.
18.4 활동: 페루 동전 던지기
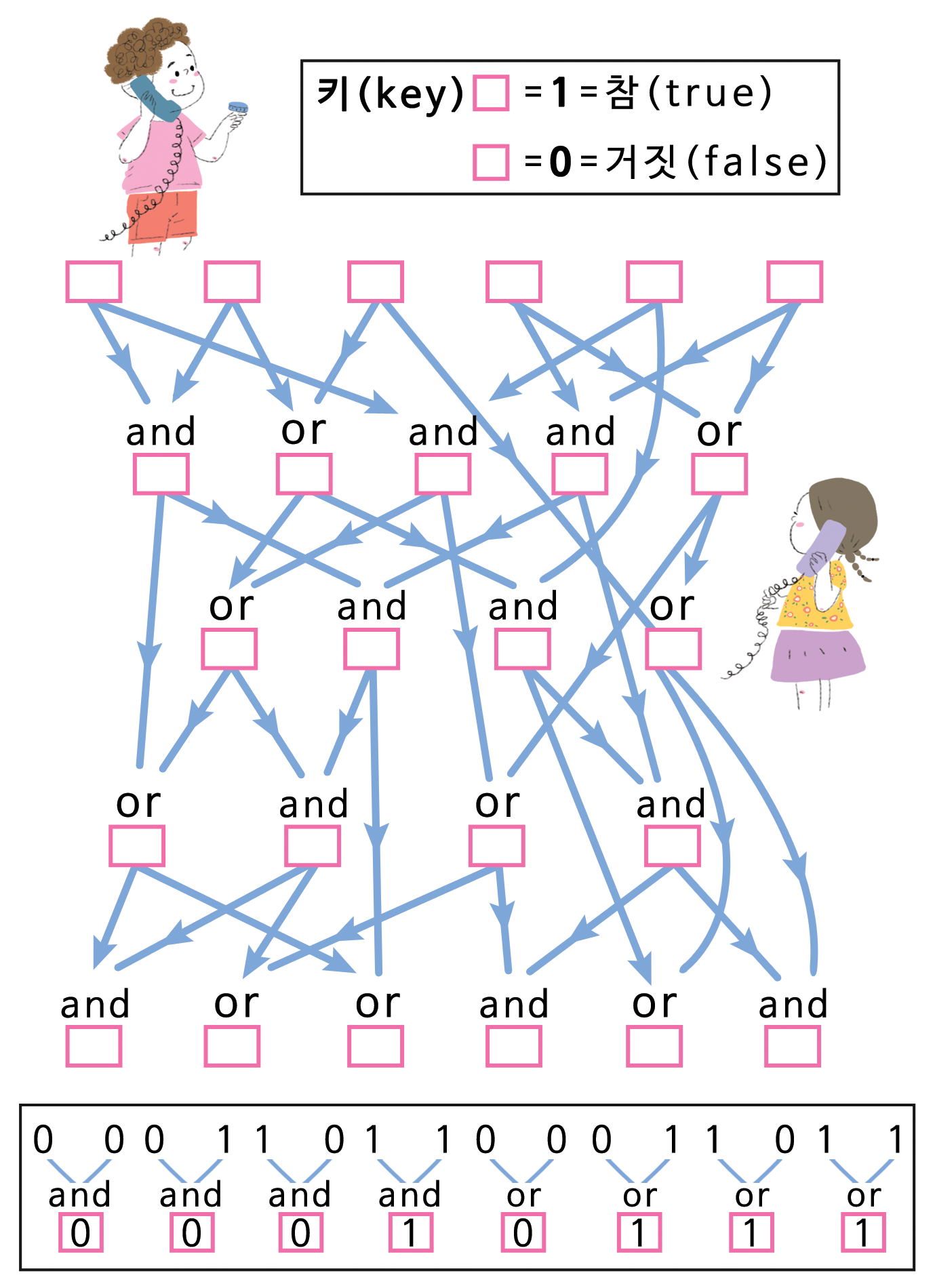
회로에 들어갈 입력값을 고르고, 출력이 무엇이 될지 풀어보라.
18.4.1 변형과 확장
- 실무에서 명백한 문제는 알리시아오 베니토 모두가 수긍할 수 있는 회로를 구축하는 협업하는 것이다. 학생들에게 이런 활동을 만드는 것은 재미가 있을지 모르지만, 실무에서는 동작하지 않는 절차로 될 수 있다— 특히, 통신선을 통해서는 더욱 그렇다. 하지만, 간단한 대안이 있는데 알리시아와 베니토가 독립적으로 회로를 구성하여 작성하고 공개하는 것이다. 그리고 나서, 알리시아가 비밀 입력을 양쪽 회로에 넣고, 상응하는 비트를 함께 비교해서 두 출력을 결합하고 난 뒤에, 만약 동일하면 1, 그렇지 않으면 0, 최종 출력값을 생성한다. 이러한 상황에서, 상대방이 속이지 않는다면, 참여자 누구도 속일 수 없다. 왜냐하면, 만약 회로 중 하나는 일방향 함수이고, 둘을 조합하면 또한 일방향 함수가 되기 때문이다.
다음 두 변형은 암호화 프로토콜 혹은 동전 던지기 문제에 관련되기 보다는 and 와 or 게이트로 구성되는 회로 아이디어와 관계있다. 컴퓨터 회로 뿐만 아니라 논리(logic)의 근본 개념을 탐색할 것이다. 이런 유형의 논리를 수학자 부울 (George Boole, 1815-64) 이름을 따서 부울 대수(Boolean algebra)라고 부른다.
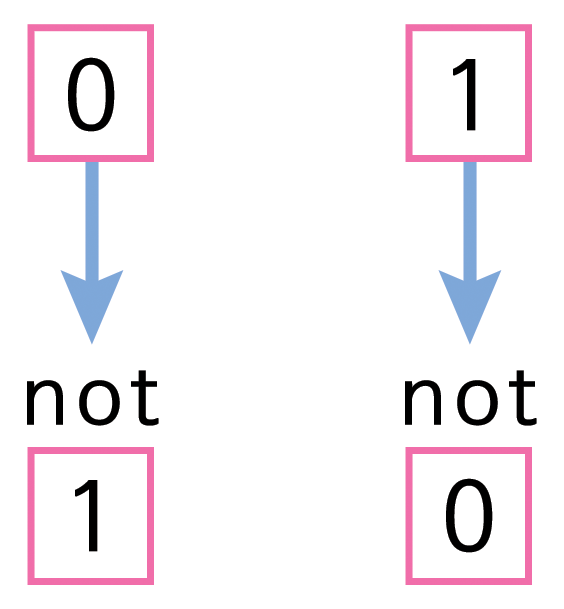
- 모든 입력이 0 이면, 000000, 출력도 모두 0 이 되고, 마찬가지로, 모든 입력이 1 이면, 111111, 모든 출력도 1 이 된다. (이런 유형의 출력을 하는 다른 입력도 물론 있다; 예를 들어, 입력이 000010 인 회로는 출력이 모두 0 이고, 110111 은 경우는 모두 1 이다.) 회로가 and와 or 게이트로 구성된 결과다. not-게이트를 추가해서, 이런 특징을 갖지 않는 회로를 구성할 수 있다. not-게이트는 출력을 입력의 반대로 한다. (즉, 0 — 1 and 1 — 0)
부울(boole)
- 다른 유형의 두가지 게이트는 and-not-게이트와 or-not-게이트로 and와 or 게이트와 같지만 뒤에 not이 붙는다. (통상 줄여서 nand-게이트, nor-게이트로 각각 줄인다.) 그래서, a > and-not b는 not(a and b)가 된다. 기능적으로 다른 회로와 차이점이 없다. 왜냐하면 해당 and-게이트, or-게이트 그리고 not으로 구션이 가능하기 때문이다. 하지만, 흥미로운 특성이 있는데 and-not-게이트로 다른 어떤 유형의 게이트도 만들 수 있고, or-not-게이트도 마찬가지다.
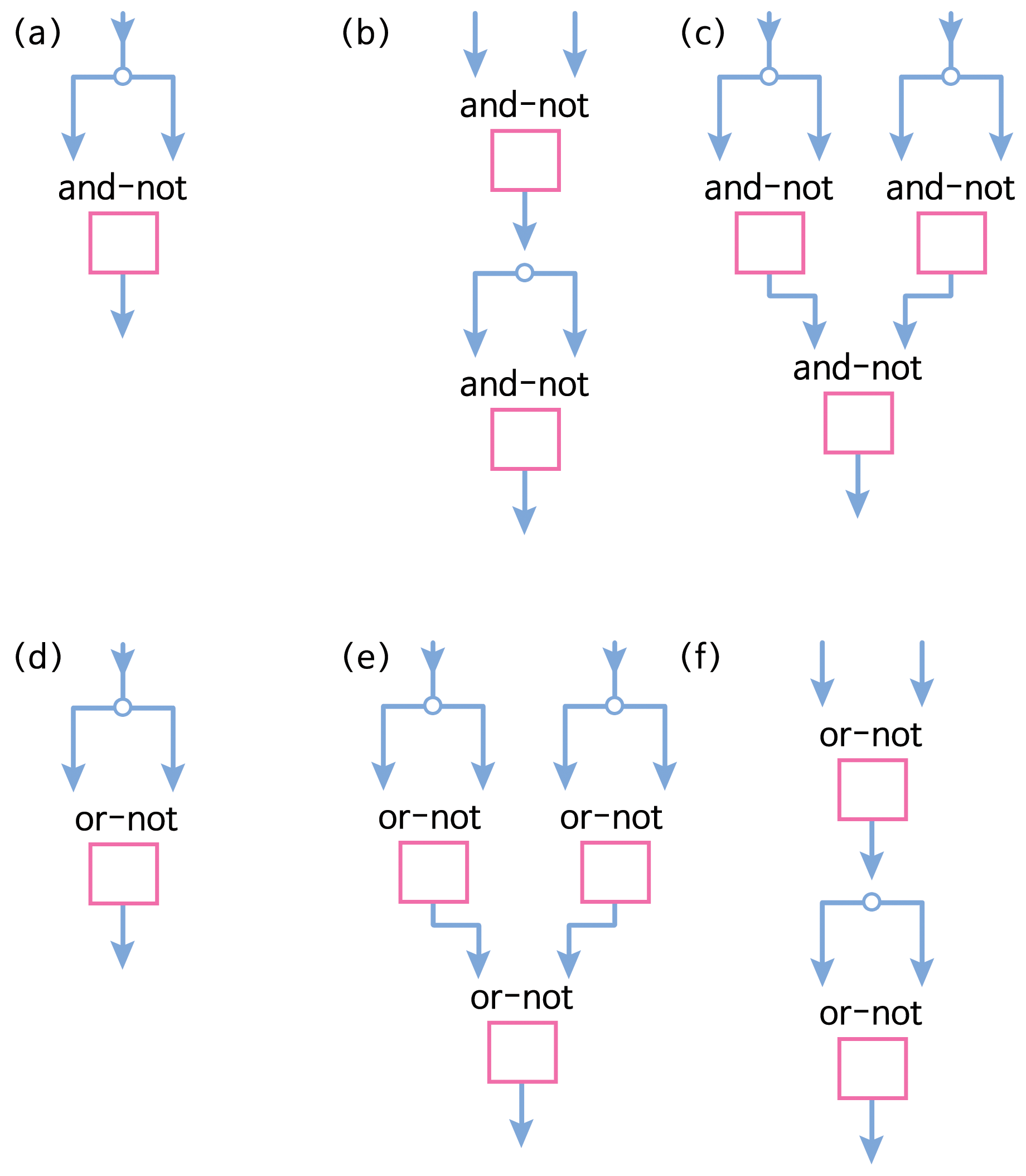
and-not-게이트와 or-not-게이트를 소개했으면, 학생들에게 도전과제로 임의의 게이트를 다른 게이트를 연결해서 구성할 수 있는지 알아보게 하라. 단지 한 유형의 게이트를 연결해서도 할 수 있는지 좀더 알아보게 하라. 다음 그림에서 기본 게이트 3개, not-게이트, and-게이트, or-게이트가 그림 상단에서 and-not-게이트로 구성되고, 그림 하단에서 or-not-게이트로 구성되는지 보여준다.
18.5 컴퓨터 과학 핵심 개념

최근에 컴퓨터 네트워크를 통한 전자상거래가 범람하고 있다. 따라서, 안전한 전자 이체, 보안 거래, 법적 구속력 있는 전자서명된 문서를 보장하는 것이 필수적이다. 암호화 분야는 안전하고 비공개 방식으로 커뮤니케이션하는 방법에 관한 것이다. 수십년 전에, 컴퓨터과학 연구원이 특정 정보를 공개하는 기법이 비밀성을 보장하는다는 다소 반직관적인 결과를 발견했다. 활동 18 키드 크립토(Kid Krypto)에서 다룰 공개키 암호시스템(public key cryptosystem)으로 정보를 교환하는데 주된 보안방식으로 널리 사용되고 있다. 예를 들어, 웹브라우져에 있는 SSL(Secure Socket Layer) 혹은 TLS(Transport Layer Security) 같은 설정이 있다; 웹브라우져가 은행같은 웹사이트에 보안 접속을 가능하게 하는 공개키 시스템이다. 누군가 송수신되는 모든 데이터를 도청할 수 있지만 보안에는 문제가 없다.
암호화는 안전하게 보관하는 것 뿐만 아니라, 다른 사람이 찾는 정보에 제한을 가하는 제어 기능과 지리적으로 멀리 떨어진 사람들 간에 신뢰를 구축하는 것도 포함된다. 암호화 거래에 대해서 공식 규칙, 즉 프로토콜(protocol)을 고안해서 위조 불가능한 전자 서명도 하고, 비밀번호를 직접 말하지 않고도 비밀정보(예를 들어, 패스워드)를 다른 사람에게 전달할 수 있게 한다. 동전던지기는 좀더 단순하지만, 처음 직면하면 불가능한 것처럼 보이지만, 유사한 문제다.
실제 상황에서, 알리시아와 베니토는 스스로 회로설계를 하지 않고 내부적으로 동작하는 컴퓨터 프로그램을 구입할 것이다. 아마도 누구도 컴퓨터 소프트웨어 내부에는 관심이 없을 것이다. 하지만, 컴퓨터 기술이 얼마나 좋은지에, 얼마나 노력을 열심히 하는데 관계없이, 둘다 의사결정 결과에 어느 쪽도 영향을 주지 못하게 확인하고 싶을 것이다.
원칙적으로, 중립적인 판사에게 분쟁을 주장해서 해결해야 한다. 판사는 회로, 알리시아의 원래 입력 이진수, 베니토에게 보낸 출력, 베니토가 답변으로 보낸 추측값을 입수한다. 정보 교환이 완료되면, 이 모든 것은 공개 정보가 된다. 따라서, 쌍방 모두 결과가 무엇인지에 대해서 합의해야 한다. 판사가 알리시아의 원래 입력 숫자를 회로에 얺고 출력값을 점검하고 의사결정이 공정했는지 결정한다. 말할 것도 없이, 규칙대로 수행되었는지 점검하는 명확한 절차가 있어서 분쟁이 일어날 것 같지 않다. 이 상황을 알리시아가 실제 동전을 던지고 베니토가 앞면 혹은 뒷면을 맞추는 상황과 비교하자— 어떤 판사도 이 사건을 수임하지 않을 것이다.
사례로 보여준 작은 회로는 실무에서 사용되지 않는데 이유는 표로 되어 있고, 속이기 쉽기 때문이다. 입력으로 32-비트 이진수를 사용하는 것이 더 나은 보호장치가 된다. 하지만, 이것 조차도 속이기 어렵다는 것을 보장하지는 않는다— 특정 회로에 달려있다. 활동 14 관광 마을에서 소개된 일방향 함수 같은 다른 방식이 사용될 수 있다. 실무에서 사용되는 방법은 큰 자연수를 인수분해하는 방법에 의존한다. (다음 활동 말미에 학습하게 되고, NP-완전하지는 않지만 매우 어려운 문제로 알려져 있다.) 한 숫자가 다른 숫자의 소인수인지 점검하는 것은 쉽지만, 매우 큰 숫자의 소인수를 찾아내는 것은 시간이 많이 걸린다. 알리시아와 베니토 (그리고 판사)가 손으로 작업하게 되면 매우 복잡하다. 실무에서 소프트웨어를 구매해서 작업한다.
전자서명도 비슷한 아이디어에 기반한다. 알리시아가 선택한 특정 보안 입력값으로 회로 출력값을 생성해서 공개함으로써, 효과적으로 그 출력값을 만든 사람이 본인임을 중명한다— 적절한 일방향 함수로 어느 누구도 입력값을 생성할 수 없다. 즉, 어느 누구도 알리시아처럼 가장할 수 없다. 실제 전자 서명을 생성하기 위해서, 좀더 복잡한 프로토콜이 필요한데, 알리시아가 특정 메시지에 서명하고 다른 사람도 알리시아 본인이 하지 않았다는 부인하지 못하도록 검증도 함께 한다. 하지만, 원리는 동일하다.
또 다른 응용사례는 통신선을 통해서 포커 게임을 하는 것이다. 카드를 돌리고 게임 참여자 양손에 든 패를 기록할 판사 같은 주심이 없는 상황이다. 모든 것이 게임 참여자 스스로 수행해야 하고, 분쟁이 있는 경우에 게임이 끝난 뒤에 판사에게 의지한다. 비슷한 상황이 진지한 계약협상에서도 일어난다. 분명하게도 참여자는 게임을 진행하는 동안에 카드 보안을 유지해야 한다. 하지만, 게임 참여자는 정직해야한다— 에이스패를 갖지 않았는데 에이스패를 가졌다고 주장하지 말아야 한다. 게임이 종료되길 기다리다, 각 게임 참여자가 다른 참여자가 가진 카드패와 게임 진행 상황을 점검하고 나서야 확인될 수 있다. 또다른 문제는 게임이 끝날 때까지 다른 게임참여자가 든 패를 비밀로 하고 카드를 돌리는 문제다. 놀랍게도, 동전 던지기와 다르지 않는 암호화 프로토콜을 사용해서 작업을 수행한다.
암호화 프로토콜은 전자 거래에서 매우 중요하다. 직불카드 소유자를 확인하고, 전자우편 발신자를 인증하고, 핸드폰 사용권한을 부여하는 등 다양하다. 이와 같은 활동을 신뢰성 있게 수행할 수 있는 능력이 전자 상거래 성공에 매우 중요하다.
18.5.1 추가 읽기
Harel이 저술한 Algorithmics 책에는 디지털 서명과 연관된 암호 프로토콜을 논의한다. 또한 어떻게 전화로 포커 게임을 하는지도 보여준다. 전화로 포커게임을 하는 것은 1981년 D.A. Klarner가 편집한 The Mathematical Gardener 책에 “Mental poker” 장에서 처음 나온 생각이다. Dorothy Denning이 저술한 Cryptography and data security는 암호학에 대한 훌륭한 컴퓨터 과학 교과서다. Dewdney가 저술한 Turing Omnibus에는 불로직에 대한 별도 섹션에서 이번 활동에 회로로 사용된 구성요소를 논의한다.